Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Dạng 1. Góc của hai véctơ
Dạng 2. Góc của hai đường thẳng
Dạng 3. Hai đương thẳng vuông góc
Bài tập trắc nghiệm hai đường thẳng vuông góc có đáp án và lời giải
Hai đường thång vuông góc
A. Câu hỏi
Câu 1. Cho hình chóp S.ABC có \(BC = a\sqrt 2 \), các cạnh còn lại đều bằng a. Góc giữa hai vectơ \(\overrightarrow {SB} \) và \(\overrightarrow {AC} \) bằng
A.
B.
C.
D.
Câu 2. Cho tứ diện ABCD có (tham khảo như hình vẽ bên).
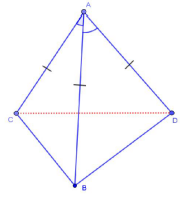
Gọi \(\varphi \) là góc giữa AB và CD. Chọm mệnh đề đúng?
A.
B.
C.
D.
Câu 3. Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Tính \(\cos \left( {\overrightarrow {BD} ,\overrightarrow {{A^\prime }{C^\prime }} } \right)\)
A. \(\cos \left( {\overrightarrow {BD} ,\overrightarrow {{A^\prime }{C^\prime }} } \right) = 0\).
B. \(\cos \left( {\overrightarrow {BD} ,\overrightarrow {{A^\prime }{C^\prime }} } \right) = 1\).
C. \(\cos \left( {\overrightarrow {BD} ,\overrightarrow {{A^\prime }{C^\prime }} } \right) = \frac{1}{2}\).
D. \(\cos \left( {\overrightarrow {BD} ,\overrightarrow {{A^\prime }{C^\prime }} } \right) = \frac{{\sqrt 2 }}{2}\).
Câu 4. Cho hình chóp O . A B C có ba cạnh OA, OB, OC đôi một vuông góc và \(OA = OB = OC = a\). Gọi M là trung điểm cạnh AB. Góc tạo bởi hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {OM} \) bằng
A.
B.
C.
D.
Câu 5. (Trường THPT Hoàng Hoa Thám – Hưng Yên, năm 2019) Cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\), biết đáy ABCD là hình vuông. Tính góc giữa \({A^\prime }C\) và BD.
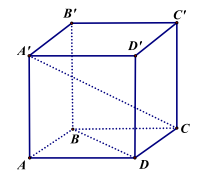
A.
B.
C.
D.
Câu 6. (Chuyên – Vĩnh Phúc – lần 3 – 2019) Cho tứ diện A B C D có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường thẳng AB và CD.
A.
B.
C.
D.
Câu 7. (THPT Trần Phú – Lần 1 – 2018-2019) Cho tứ diện đều ABCD có cạnh bằng a. Giá trị tích vô hướng \(\overrightarrow {AB} (\overrightarrow {AB} – \overrightarrow {CA} )\) bằng
A. \(\frac{{{a^2}}}{2}\).
B. \(\frac{{{a^2}\sqrt 2 }}{2}\).
C. \(\frac{{{a^2}\sqrt 3 }}{2}\).
D. \(\frac{{3{a^2}}}{2}\).
Câu 8. Cho hình lăng trụ tam giác đều \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có tất cả các cạnh đều bằng a, cosin góc giữa hai đường thẳng \(A{B^\prime }\) và \(B{C^\prime }\) bằng
A. \(\frac{1}{4}\).
B. \(\frac{{\sqrt 2 }}{4}\).
C. \(\frac{1}{2}\).
D. \(\frac{3}{4}\).
Câu 9. Cho hình chóp O.ABC có ba cạnh OA, OB, OC đôi một vuông góc và \(OA = OB = OC = a\). Gọi M là trung điểm cạnh AB. Góc hợp bởi hai véc tơ \(\overrightarrow {BC} \) và \(\overrightarrow {OM} \) bằng
A.
B.
C.
D.
Câu 10. Cho hình lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy ABC là tam giác đều cạnh a, tam giác \({A^\prime }BC\) đều nằm trong mặt phẳng vuông góc với (ABC). M là trung điểm cạnh \(C{C^\prime }\). Tính cosin góc \(\alpha \) giữa hai đường thẳng \(A{A^\prime }\) và BM.
A. \(\cos \alpha = \frac{{2\sqrt {22} }}{{11}}\).
B. \(\cos \alpha = \frac{{\sqrt {33} }}{{11}}\).
C. \(\cos \alpha = \frac{{\sqrt {11} }}{{11}}\).
D. \(\cos \alpha = \frac{{\sqrt {22} }}{{11}}\).
Câu 11. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC, AD. Biết \(AB = 2a,CD = 2a\sqrt 2 \) và \(MN = a\sqrt 5 \). Số đo góc giữa hai đương thẳng AB và CD là
A.
B.
C.
D.
Câu 12. (THPT THUẬN THÀNH 1) Cho hình chóp S.ABC có \(SA = SB = SC = AB = AC = a\) và góc . Côsin góc tạo bởi hai đường thẳng AB và SC gần nhất với giá trị nào sau đây?
A. 0,83 .
B. 0,37 .
C. 0,45 .
D. 0,71 .
Câu 13. (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng a và ABCD là hình vuông. Gọi M là trung điểm của CD. Giá trị \(\overrightarrow {MS} \cdot \overrightarrow {CB} \) bằng
A. \(\frac{{{a^2}}}{2}\).
B. \( – \frac{{{a^2}}}{2}\).
C. \(\frac{{{a^2}}}{3}\).
D. \(\frac{{\sqrt 2 {a^2}}}{2}\).
Câu 14. (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Cho hình chóp S.ABC có AB=AC, \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng SA và BC.
A.
B.
C.
D.
Dạng 2. Góc của hai đường thẳng
Câu 15. (Chuyên Thái Bình lần 2 – 2018-2019) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Tính góc giữa hai đường thẳng AC và \({A^\prime }B\).
A.
B.
C.
D.
Câu 16. (THPT CHUYÊN HÙNG VƯƠNG – PHÚ THỌ – LẦN 1 – 2018) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Góc giữa hai đường thẳng \(B{A^\prime }\) và CD bằng:
A.
B.
C.
D.
Câu 17. (THPT Chuyên ĐH Vinh – GK – năm 2017 – 2018) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với \(AB = 2a,BC = a\). Các cạnh bên của hình chóp cùng bằng \(a\sqrt 2 \). Tính góc giữa hai đường thẳng AB và SC.
A.
B.
C.
D.
Câu 18. (THPT CHUYÊN NGỮ – HÀ NỘI – 2018) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Góc giữa hai đường thẳng \({A^\prime }{C^\prime }\) và BD bằng.
A.
B.
C.
D.
Câu 19. (THPT THANH MIỆN I – HẢI DU’ƠNG – LẦN 1 – 2018) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\), góc giữa hai đường thẳng \({A^\prime }B\) và \({B^\prime }C\) là
A.
B.
C.
D.
Câu 20. (THTP LÊ QUÝ ĐÔN – HÀ NÔI – LẦN 1 – 2018) Cho hình lăng trụ đều \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có cạnh đáy bằng 1 , cạnh bên bằng 2 . Gọi \({C_1}\) là trung điểm của \(C{C^\prime }\). Tính côsin của góc giữa hai đường thẳng \(B{C_1}\) và \({A^\prime }{B^\prime }\).
A. \(\frac{{\sqrt 2 }}{6}\).
B. \(\frac{{\sqrt 2 }}{4}\).
C. \(\frac{{\sqrt 2 }}{3}\).
D. \(\frac{{\sqrt 2 }}{8}\).
Câu 21. (THPT HÀ HUY TẠP – LẦN 2 – 2018) Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD là
A.
B.
C.
D.
Câu 22. (THPT QUỲNH LƯU – NGHỆ AN – 2018) Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ;CD) bằng:
A.
B.
C.
D.
Câu 23. (CHUYÊN VINH – LẦN 2 – 2018) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) (hình vẽ bên dưới). Góc giữa hai đường thẳng AC và \({A^\prime }D\) bằng
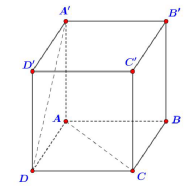
A.
B.
C.
D.
Câu 24. (SGD Nam Định) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) cạnh a. Gọi M là trung điểm của CD và N là trung điểm của \({A^\prime }{D^\prime }\). Góc giữa hai đường thẳng \({B^\prime }M\) và \({C^\prime }N\) bằng
A.
B.
C.
D.
Câu 25. Cho tứ diện OABC có \(OA = OB = OC = a;OA,OB,OC\) vuông góc với nhau từng đôi một. Gọi I là trung điểm BC. Tính góc giữa hai đường thẳng AB và OI.
A.
B.
C.
D.
Câu 26. Cho hình hình lăng trụ \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình chữ nhật và. Sô đo góc giữa hai đường thẳng AC và \({B^\prime }{D^\prime }\) là
A.
B.
C.
D.
Câu 27. (Chuyên Đại học Vinh – Lần 1 – Năm học 2018 – 2019) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có I, J lần lượt là trung điểm của BC và \(B{B^\prime }\). Góc giữa hai đường thẳng AC và IJ bằng
A.
B.
C.
D.
Câu 28. (Thi thử cụm Vũng Tàu – 2019) Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Góc giữa hai đường thẳng AC và \(D{A^\prime }\) bằng
A.
B.
C.
D.
Câu 29. Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Tính góc giữa hai đường thẳng \(A{B^\prime }\) và \({A^\prime }{C^\prime }\).
A.
B.
C.
D.
Câu 30. Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Góc giữa hai đường thẳng \(A{B^\prime }\) và \(C{D^\prime }\) bằng
A.
B.
C.
D.
Câu 31. Cho hình chó S.ABCD có đáy là hình thoi cạnh \(a,SA = a\sqrt 3 \) và \(SA \bot BC\). Góc giữa hai đường thẳng SD và BC bằng
A.
B.
C.
D.
Câu 32. Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) (hình vẽ bên dưới). Góc giữa hai đường thẳng AC và \({A^\prime }D\) bằng
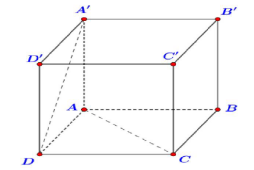
A.
B.
C.
D.
Câu 33. Cho hình lăng trụ đều \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có tất cả các cạnh bằng a. Góc giữa hai đường thẳng \(B{C^\prime }\) và \({B^\prime }{D^\prime }\) bằng
A.
B.
C.
D.
Câu 34. Cho tứ diện ABCD có \(AB = CD = 2a\). Gọi M, N lần lượt là trung điểm của AD và BC. Biết \(MN = \sqrt 3 a\), góc giữa hai đường thẳng AB và CD bằng
A.
B.
C.
D.
Câu 35. (Thi giữa kì II – 1819 Chuyên Lê Hồng Phong Nam Định) Cho hình chóp tứ giác S.ABCD có có đáy là hình vuông cạnh 2a; cạnh SA=a và vuông góc với đáy. Gọi M là trung điểm CD. Tính \(\cos \alpha \) với \(\alpha \) là góc tạo bởi SB và AM.
A. \( – \frac{2}{5}\).
B. \(\frac{1}{2}\).
C. \(\frac{2}{5}\).
D. \(\frac{4}{5}\).
Câu 36. (THPT Ngô Quyền – Ba Vì – Hải Phòng, lần 1) Cho hình lăng trụ tam giác đều \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có \(AB = a\) và \(A{A^\prime } = a\sqrt 2 \). Góc giữa hai đường thẳng \(A{B^\prime }\) và \(B{C^\prime }\) bằng
A.
B.
C.
D.
Câu 37. (Tham khảo 2018) Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC ( tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng 0M và AB bằng
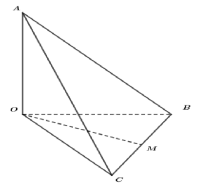
A.
B.
C.
D.
Câu 38. Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\); gọi M là trung điểm của \({B^\prime }{C^\prime }\). Góc giữa hai đường thẳng AM và \(B{C^\prime }\) bằng
A.
B.
C.
D.
Câu 39. [THPT NINH BINH-BẠC LIÊU-2019] Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Gọi M là trung điểm của \(D{D^\prime }\) (Tham khảo hình vẽ). Tính cô-sin của góc giữa hai đường thẳng \({B^\prime }C\) và \({C^\prime }M\).
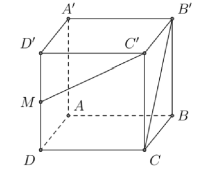
A. \(\frac{1}{{\sqrt {10} }}\).
B. \(\frac{1}{3}\).
C. \(\frac{1}{{\sqrt 3 }}\).
D. \(\frac{{2\sqrt 2 }}{9}\).
Xem thêm