50 Bài tập Phép đồng dạng (có đáp án)- Toán 11

Bài tập Toán 11 Chương 1 Bài 8: Phép đồng dạng 

A. Bài tập Phép đồng dạng

I. Bài tập trắc nghiệm

Bài 1: Cho hình thoi ABCD tâm O. Gọi E, F, M, N lần lượt là trung điểm các cạnh AB, CD, BC, AD. P là phép đồng dạng biến tam giác OCF thành tam giác CAB. Tìm mệnh đề sai trong các mệnh đề sau:

A. P hợp thành bởi phép đối xứng tâm O và phép vị tự tâm A tỉ số k = 2

B. P hợp thành bởi phép đối xứng trục AC và phép vị tự tâm C tỉ số k = 2

 

C. P hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm O

D. P hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O tỉ số k = -1

Lời giải:

Đáp án: D

A. ĐO(∆OCF) = ∆OAE; V(O; 2)(∆AOE) = ∆CAB

B. ĐAC(∆OCF) = ∆OCM; V(O; 2)(∆OCM) = ∆ACB

C. V(C; 2)(∆OCF) = ∆ACD; ĐO(∆ACD) = ∆ACB

D. ĐBD(∆OCF) = ∆OAN; V(O; -1)(∆OAN) = ∆OCM

Bài 2: Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ.

A.(8; -3)      

B. (-8;3)      

C. (-8;-3)      

D. (3;8)

Lời giải:

Đáp án: D

(hình 2) V(I; -2)(M(-1;0)) = M'(8;3); ĐOx(M’) = M”(8; -3)

Bài 3: Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x – y – 1 = 0 thành đường thẳng d’ có phương trình.

 

A. x – y + 3 = 0

B. x + y – 3 = 0

C. x + y + 3 = 0

D. x – y + 2 = 0

Lời giải:

Đáp án: B

(hình 3) phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M(1;0) thành điểm M’(3;0) ⇒ biến d: x – y – 1 = 0. Phép đối xứng trục Ox, biến đường thẳng d’ thành d’’: x + y – 3 = 0

Bài 4: Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:

A. AIFD      

B. BCFI      

C. CIEB      

D. DIEA

Lời giải:

Đáp án: C

V(C;2)(IGHF) = (AIFD); Đ1(AIFD) = CIEB. Đáp án C.

Bài 5: Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = $\frac{1}{2}$ và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ.

A.(2;-1)      

B. (8;1)

C.(4;-2)      

D. (8;4)

Lời giải:

Đáp án: A

V(0;$\frac{1}{2}$)(M(4;2)) = M'(2;1);

ĐOx(M'(2;1)) = M”(2;-1). Đáp án A.

II. Bài tập tự luận có lời giải

Bài 1 Cho tam giác ABC. Dựng ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm B có tỉ số $\frac{1}{2}$ và phép đối xứng qua đường trung trực của BC.

Lời giải:

• ΔABC qua phép vị tự tâm B, tỉ số $\frac{1}{2}$:

• ΔA’BC’ qua phép đối xứng trục Δ (Δ là trung trực của BC).

Đ_Δ (A’) = A” (như hình vẽ).

Đ_Δ (B) = C

Đ_Δ (C’) = C’.

Vậy ảnh của tam giác ABC thu được sau khi thực hiện phép vị tự tâm B tỉ số $\frac{1}{2}$ và phép đối xứng qua Δ là ΔA’’C’C.

Bài 2 Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L, J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh rằng hai hình thang JLKI và IHDC đồng dạng với nhau.

Lời giải:

+ I là trung điểm AC; BD; HK

⇒ Đ_I(H) = K ; Đ_I(D) = B ; Đ_I (C) = A.

⇒ Hình thang IKBA đối xứng với hình thang IHDC qua I (1)

+ J; L; K; I lần lượt là trung điểm của CI; CK; CB; CA

⇒ Hình thang JLKI là ảnh của hình thang IKBA qua phép vị tự tâm C tỉ số $\frac{1}{2}$.

⇒ Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép vị tự tâm C tỉ số $\frac{1}{2}$.

⇒ IJKI và IHDC đồng dạng.

Bài 3 Trong mặt phẳng Oxy cho điểm I(1; 1) và đường tròn tâm I bán kính 2. Viết phương trình đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc 45^o và phép vị tự tâm O, tỉ số căn 2 .

Lời giải:

+ Gọi (I₁; R₁) = Q_{(O; 45º)} (I; R) (Phép quay đường tròn tâm I, bán kính R qua tâm O một góc 45º).

Vậy phương trình đường tròn cần tìm là (I₂; R₂): x² + (y – 2)² = 8.

Bài 4 Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A, tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.

Lời giải:

Gọi d là đường phân giác của góc B của ΔABC.

+ Phép đối xứng qua d: biến H thành H’ ∈ AB, biến A thành A’ ∈ BC; biến B thành B

(Dễ dàng nhận thấy H’ ∈ BA; A’ ∈ BC).

⇒ ΔH’BA’ = Đ_d(ΔHBA).

⇒ ΔH’BA’ = ΔHBA.

Mà ΔABC  ΔHBA theo tỉ số 

⇒ ΔABC  ΔH’BA’ theo tỉ số k

⇒ AB = k.H’B; BC = k.BA’.

Mà A ∈ tia BH’ ; C ∈ tia BA’

Vậy phép đồng dạng cần tìm là phép vị tự tâm B, tỉ số  hợp với phép đối xứng trục d là phân giác của 

III. Bài tập vận dụng

Bài 1 Cho tam giác ABC. Xác định ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm B tỉ số  và phép đối xứng qua đường trung trực của BC

Bài 2 Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hai hình thang JLKI và IHDC đồng dạng với nhau.

Bài 3 Trong mặt phẳng Oxy cho điểm I (1;1) và đường trong tâm I bán kính 2. Viết phương trình của đường trong là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc  và phép vị tự tâm O,tỉ số .

Bài 4 Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A. Tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC

Bài 5 Mọi phép dời hình cũng là phép đồng dạng với tỉ số k bằng?

Bài 6 Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành?

Bài 7 Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = $\frac{1}{2}$ và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ.

Bài 8 Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ.

Bài 9 Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x – y – 1 = 0 thành đường thẳng d’ có phương trình.

Bài 10 Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ

B. Lý thuyết Phép đồng dạng

. Định nghĩa

 

– Định nghĩa: Phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0), nếu với hai điểm M, N bất kì và ảnh M’, N’ tương ứng của chúng ta luôn có M’N’ = kMN.

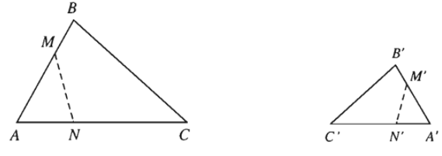
– Nhận xét

1) Phép dời hình là phép đồng dạng tỉ số 1.

2) Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

II. Tính chất

Phép đồng dạng tỉ số k:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

 

d) Biến đường tròn bán kính R thành đường tròn có bán kính kR.

– Chú ý.

a) Nếu một phép đồng dạng biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

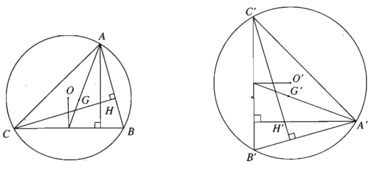
b) Phép đồng dạng biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thảng đỉnh, biến cạnh thành cạnh.

Ví dụ 1. Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 đường tròn (C) và (C’) có phương trình x² + y² – 4y – 5 = 0 và x² + y² – 2x + 2y – 14 = 0. Gọi (C’) là ảnh của (C) qua phép đồng dạng tỉ số k, khi đó giá trị k là ?

Lời giải:

Đường tròn (C) có tâm I(0 ; 2) bán kính R = 3.

Đường tròn (C’) có tâm I’(1 ; – 1) bán kính R’ = 4.

Ta có (C’) là ảnh của (C) qua phép đồng dạng tỉ số k nên : 4 = 3k

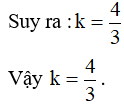
III. Hình đồng dạng

– Định nghĩa. Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.

– Ví dụ 2. Các hình sau đôi một đồng dạng với nhau.