50 Bài tập Hàm số lượng giác (có đáp án) – Toán 11

Bài tập Toán 11 Chương 1 Bài 1: Hàm số lượng giác

A. Bài tập Hàm số lượng giác

I. Bài tập trắc nghiệm

Bài 1. Hàm số :

có tập xác định là:

A. R

B. R\{k2π, k ∈ Z}.

C. {k2π, k ∈ Z}.

D. ∅

Lời giải:

Chọn đáp án C

Bài 2. Hàm số y = sinxcos2x là:

A. Hàm chẵn.

B. Hàm không có tính chẵn, lẻ.

C. Hàm không có tính tuần hoàn.

D. Hàm lẻ.

Lời giải:

Chọn đáp án D

Bài 3. Hàm số  thỏa mãn tính chất nào sau đây?

A. Hàm chẵn.

B. Hàm không có tính chẵn, lẻ.

C. Xác định trên R.

D. Hàm lẻ.

Lời giải:

Chọn đáp án A

Bài 4. Trong các hàm số sau, hàm số nào là hàm lẻ?

A. y = sin2x

B. y = sin2x.cosx.

C. y = $\frac{\tan x}{\cos x}$

D. y = $\frac{cotx}{\sin x}$

Lời giải:

Chọn đáp án C

Bài 5. Trong các hàm số sau, hàm số nào là hàm chẵn?

A. 

B. y = sinx.cos2x

C. y = cosx.sin²x

D. y = cosxsin3x.

Lời giải:

Do y = sin²x và y = cosx là hàm chẵn nên hàm số y = cosx. sin²x là hàm chẵn.

Chọn đáp án C

Bài 6. Hàm số y = $\frac{\cos x}{\left(2\sin x–\sqrt{3}\right)}$ có tập xác định là:

A. R\{$\frac{\pi }{3}$+k2π, k ∈ Z}.

B. R\{$\frac{\pi }{6}$+kπ, k ∈ Z}.

C. R\{$\frac{\pi }{6}$+k2π, $\frac{5\pi }{6}$+k2π, k ∈ Z}.

D. R\{$\frac{\pi }{3}$+k2π, $\frac{2\pi }{3}$+k2π, k ∈ Z}.

Lời giải:

Chọn đáp án D

Bài 7. Hàm số y = tan$\frac{x}{2}–\frac{\pi }{4}$ có tập xác định là:

A. R\{$\frac{\pi }{2}$+k2π, k ∈ Z}.

B. R\{$\frac{\pi }{2}$+kπ, k ∈ Z}.

C. R\{$\frac{3\pi }{2}$+k2π, k ∈ Z}.

D. R.

Lời giải:

Chọn đáp án C

Bài 8. Tập xác định của hàm số y = cot(2x – $\frac{\pi }{3}$) + 2 là:

A. R\{$\frac{\pi }{6}$+kπ, k ∈ Z}.

B. R\{$\frac{\pi }{6}$+k2π, k ∈ Z}.

C. R\{$\frac{5\pi }{12}$+$\frac{k\pi }{2}$, k ∈ Z}.

D. R\{$\frac{\pi }{6}$+$\frac{k\pi }{2}$, k ∈ Z}.

Lời giải:

Chọn đáp án D

Bài 9. Hàm số :

có tập xác định là:

A. R\{kπ, k ∈ Z}.

B. R\{$\frac{\pi }{2}$+π, k ∈ Z}.

C. R\{$\frac{\pi }{2}$+k2π, k ∈ Z}.

D. R\{$\frac{k\pi }{2}$, k ∈ Z}.

Lời giải:

Chọn đáp án C

Bài 10. Cho hàm số y = $\frac{\sin x}{1+\tan x}$ và k ∈ Z.

Khoảng nào dưới đây không nằm trong tập xác định của hàm số?

Lời giải:

Nên khoảng này không nằm trong tập xác định của hàm số

II. Bài tập tự luận có lời giải

Bài 1: Giá trị nhỏ nhất của hàm số y = 3- 4sin²xcos²x là:

Lời giải:

Bài 2: Hàm số y = $\sqrt{1–{\cos }^{2}x}$ có chu kì là:

Lời giải:

Tập xác định của hàm số đã cho là R mà cos²x có chu kì là π nên y= $\sqrt{1–{\cos }^{2}x}$ cũng có chu kì là π

Bài 3:Hai hàm số nào sau đây có chu kì khác nhau?

Lời giải:

Hàm số sinx có chu kì là 2π, hàm số tanx có chu kì là π

Vậy hai hàm số y = sinx và y = tan x có chu kì khác nhau.

Bài 4: Chu kì của hàm số y = 2sin(2x + $\frac{\pi }{3}$) -3cos(2x – $\frac{\pi }{4}$) là:

Lời giải:

Bài 5: Chu kì của hàm số y = sin²x -2cos³x là:

Lời giải:

Chu kì của hàm số y=sin²x là π, chu kì của hàm số y=cos³x là ($\frac{2\pi }{3}$ nên chu kì của hàm số đã cho là 2π

Bài 6: Trong các hàm số sau, hàm số nào không là hàm chẵn và cũng không là hàm lẻ?

Lời giải:

Xét phương án B:

Do đó, hàm số đã cho không là hàm chẵn và cũng không phải là hàm lẻ

Bài 7: Hàm số y = (sinx + cosx)² + cos2x có giá trị lớn nhất là:

Lời giải:

Ta có:

Suy ra hàm số có giá trị lớn nhất là 1 + $\sqrt{2}$

Bài 8: Hàm số y = $\sqrt{3}$sinx – cosx có giá trị nhỏ nhất là:

Lời giải:

Bài 9: Cho hàm số y = $\frac{\cos x–1}{\cos x+2}$. Mệnh đề nào trong số các mệnh đề sau đây là sai?

Lời giải:

Bài 10: Hàm số nào sau đây có giá trị lớn nhất bằng 2?

Lời giải:

Các hàm số y= tanx- cotx và y= 2tanx không có giá trị lớn nhất, hàm số y= sin(2x-$\frac{\pi }{4}$) có giá trị lớn nhất là 1

Cũng có thể nhận ngay ra đáp án C vì :

III. Bài tập vận dụng

Bài 1 Hãy xác định các giá trị của x trên đoạn [-π; $\frac{3\pi }{2}$] để hàm số y = tanx

a) Nhận giá trị bằng 0

b) Nhận giá trị bằng 1

c) Nhận giá trị dương

d) Nhận giá trị âm.

Bài 2 Tìm tập xác định của các hàm số:

Bài 3 Dựa vào đồ thị hàm số y = sinx, hãy vẽ đồ thị của hàm số y = |sinx|.

Hướng dẫn giải bài 3:

Ta có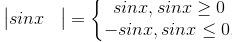 

Mà sinx < 0 ⇔ x ∈ (π + k2π, 2π + k2π), k ∈ Z nên lấy đối xứng qua trục Ox phần đồ thị của hàm số y = sinx trên các khoảng này còn giữ nguyên phần đồ thị hàm số y = sinx trên các đoạn còn lại ta được đồ thị của hàm số y = IsinxI

Bài 4 Chứng minh rằng sin2(x + kπ) = sin ²x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin²x

Bài 5 Dựa vào đồ thị hàm số y = cosx, tìm các giá trị của x để cosx = $\frac{1}{2}$

Bài 6 Dựa vào đồ thị hàm số y = sinx, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.

Bài 7 Hãy xác định các giá trị của x trên đoạn $[-\pi ;\frac{3\pi }{2}]$ để hàm số $y=\tan x$

a) Nhận giá trị bằng 0.

b) Nhận giá trị bằng 1.

c) Nhận giá trị dương.

d) Nhận giá trị âm.

Bài 8 Tìm tập xác định của hàm số

a) $y=\frac{1+\cos x}{\sin x}$.

b) $y=\sqrt{\frac{1+\cos x}{1-\cos x}}$.

c) $y=\tan (x-\frac{\pi }{3})$.

d) $y=\cot (x+\frac{\pi }{6})$.

Bài 9 Dựa vào đồ thị hàm số y = sinx, hãy vẽ đồ thị của hàm số y = |sinx|

Bài 10 Chứng minh rằng sin2(x + kπ) = sin ²x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin²x.

B. Lý thuyết Hàm số lượng giác

I. Định nghĩa

1. Hàm số sin và hàm số côsin

a) Hàm số sin

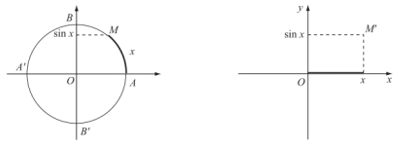
– Quy tắc đặt tương ứng mỗi số thực x với số thực sinx

được gọi là hàm số sin, kí hiệu là y = sinx.

Tập xác định của hàm số sin là $\mathrm{ℝ}$.

b) Hàm số côsin

– Quy tắc đặt tương ứng mỗi số thực x với số thực cosx:

được gọi là hàm số côsin, kí hiệu là y = cosx.

Tập xác định của hàm số côsin là $\mathrm{ℝ}$.

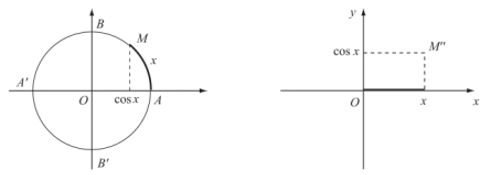
2. Hàm số tang và hàm số côtang

a) Hàm số tang

Hàm số tang là hàm số được xác định bởi công thức: $y=\frac{\sin x}{\text{cosx\hspace{0.17em}\hspace{0.17em}}}(\text{}c\text{osx}\ne \text{0)}$

Kí hiệu là y = tanx.

Vì cosx ≠ 0 khi và chỉ khi $x\ne \frac{\pi }{2}+k\pi (k\in \mathbb{Z})$ nên tập xác định của hàm số y = tanx là $D=ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$.

b) Hàm số côtang

Hàm số côtang là hàm số được xác định bởi công thức: $y=\frac{\text{cos}x}{\text{sin x\hspace{0.17em}\hspace{0.17em}}}(\sin \text{\hspace{0.17em}x}\ne \text{0)}$

Kí hiệu là y = cot x.

Vì sinx ≠ 0 khi và chỉ khi $x\ne k\pi (k\in \mathbb{Z})$ nên tập xác định của hàm số y = cotx là $D=ℝ\backslash \left\{k\pi ;k\in \mathbb{Z}\right\}$ .

– Nhận xét:

Hàm số y = sinx là hàm số lẻ, hàm số y = cosx là hàm số chẵn. Từ đó, suy ra các hàm số y = tanx và y = cotx là những hàm số lẻ.

II. Tính tuần hoàn của hàm số lượng giác

– Số T = 2π là số dương nhỏ nhất thỏa mãn đẳng thức: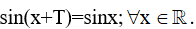 

– Hàm số y = sinx thỏa mãn đẳng thức trên được gọi là hàm số tuần hoàn với chu kì 2π.

– Tương tự; hàm số y = cosx là hàm số tuần hoàn với chu kì 2π.

– Các hàm số y = tanx và y = cotx cũng là những hàm số tuần hoàn, với chu kì π.

III. Sự biến thiên và đồ thị của hàm số lượng giác.

1. Hàm số y = sinx.

Từ định nghĩa ta thấy hàm số y = sinx :

+ Xác định với mọi x$\in \mathrm{ℝ}$ và – 1 ≤ sinx ≤ 1.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì 2π.

Sau đây, ta sẽ khảo sát sự biến thiên của hàm số y = sinx.

a) Sự biến thiên và đồ thị hàm số y = sinx trên đoạn [0; π].

Hàm số y = sinx đồng biến trên $\left[0;\frac{\pi }{2}\right]$ và nghịch biến trên $\left[\frac{\pi }{2};\pi \right]$.

Bảng biến thiên:

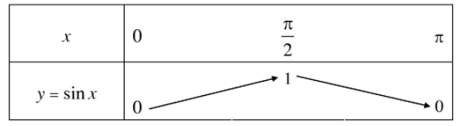
Đồ thị của hàm số y = sinx trên đoạn [0; π] đi qua các điểm (0; 0); (x₁; sinx₁); (x₂; sinx₂); (x₃; sinx₃); (x₄; sinx₄); (π; 0).

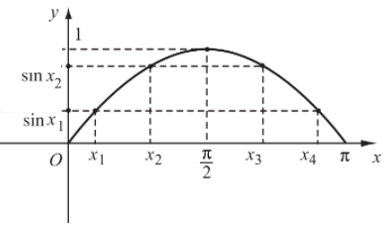
– Chú ý:

Vì y = sinx là hàm số lẻ nên lấy đối xứng đồ thị hàm số trên đoạn [0; π] qua gốc tọa độ O, ta được đồ thị hàm số trên đoạn [– π;  0].

Đồ thị hàm số y = sinx trên đoạn [– π; π] được biểu diễn như hình vẽ dưới đây:

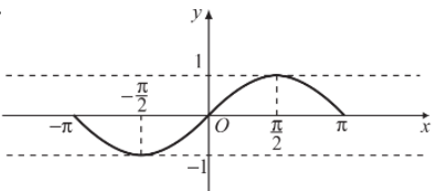
b) Đồ thị hàm số y = sinx trên $\mathrm{ℝ}$.

Hàm số y = sinx là hàm số tuần hoàn với chu kì 2π nên với mọi x ta có:

$\sin (x+\text{\hspace{0.17em}}k2\pi )=\sin x;k\in \mathbb{Z}$

Do đó, muốn có đồ thị  hàm số y = sinx trên toàn bộ tập xác định , ta tịnh tiến liên tiếp đồ thị hàm số trên đoạn [– π; π] theo các vecto $\overrightarrow{v}=(2\pi ;0)$ và $-\overrightarrow{v}=(-2\pi ;0)$, nghĩa là tịnh tiến song song với trục hoành từng đoạn có độ dài 2π.

Dưới đây là đồ thị hàm số y = sinx trên $\mathrm{ℝ}$:

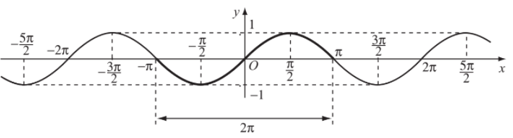
c) Tập giá trị của hàm số y = sinx

Tập giá trị của hàm số này là [– 1; 1].

2. Hàm số y = cosx.

Từ định nghĩa ta thấy hàm số y = cosx:

+ Xác định với mọi x$\in \mathrm{ℝ}$  và – 1 ≤  cosx  ≤  1.

+ Là hàm số chẵn.

+ Là hàm số tuần hoàn với chu kì 2π.

Với mọi x$\in \mathrm{ℝ}$ ta có: $\sin \left(x+\text{\hspace{0.17em}\hspace{0.17em}}\frac{\pi }{2}\right)=c\text{os x}$.

Từ đó, bằng cách tịnh tiến đồ thị hàm số y = sinx theo vecto $\overrightarrow{u}=\left(\frac{-\pi }{2};0\right)$ (sang trái một đoạn có độ dài bằng $\frac{\mathrm{\pi }}{2}$, song song với trục hoành), ta được đồ thị hàm số  y = cos x.

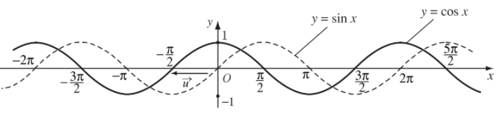
+ Hàm số y = cos x đồng biến trên đoạn [– π; 0] và nghịch biến trên đoạn [0; π].

+ Bảng biến thiên:

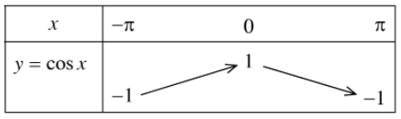
+ Tập giá trị của hàm số y = cosx là [– 1; 1].

+ Đồ thị của các hàm số y = cosx; y = sinx được gọi chung là các đường hình sin.

3. Hàm số y = tanx.

Từ định nghĩa hàm số y = tan x:

+ Có tập xác định: $D=ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

a) Sự biến thiên và đồ thị hàm số y = tanx trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$

+ Hàm số y = tanx đồng biến trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$.

+ Bảng biến thiên:

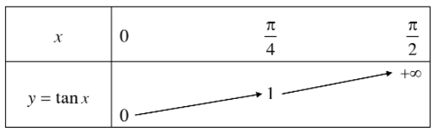
+ Bảng giá trị:

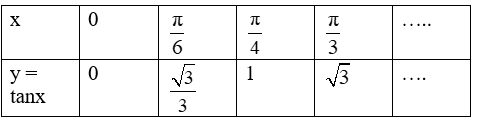
Đồ thị hàm số y = tanx trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$ đi qua các điểm tìm được.

b) Đồ thị hàm số y = tanx trên D.

Vì y = tanx là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc tọa độ O. Lấy  đối xứng qua tâm O đồ thị hàm số y = tanx trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$, ta được đồ thị hàm số trên nửa khoảng $\left(\frac{-\pi }{2};0\right]$.

Từ đó, ta được đồ thị hàm số y = tanx trên khoảng $\left(\frac{-\pi }{2};\frac{\pi }{2}\right)$.

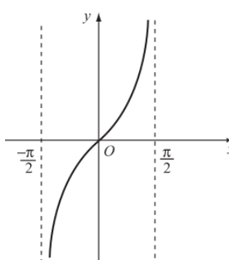
– Vì hàm số y = tanx tuần hoàn với chu kì π nên tịnh tiến đồ thị hàm số trên khoảng $\left(\frac{-\pi }{2};\frac{\pi }{2}\right)$ song song với trục hoành từng đoạn có độ dài π, ta được đồ thị hàm số y = tanx trên D.

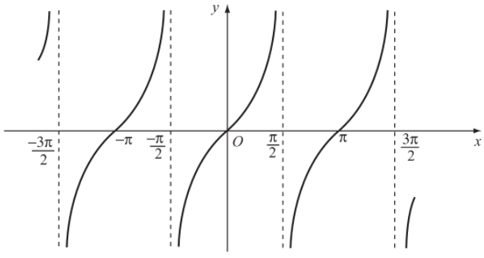
+ Tập giá trị của hàm số y = tanx là $(-\infty ;+\text{}\infty )$.

4. Hàm số y = cot x

Hàm số y = cotx: 

+ Có tập xác định là $D=ℝ\backslash \left\{k\pi ;k\in \mathbb{Z}\right\}$.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

a) Sự biến thiên của hàm số y = cotx trên khoảng (0; π).

Hàm số y = cotx nghịch biến trên khoàn (0; π).

Bảng biến thiên:

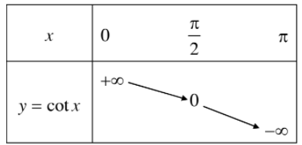
Hình biểu diễn của hàm số y = cotx trên khoảng (0; π).

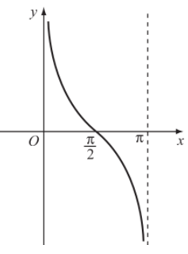
b) Đồ thị hàm số y = cotx trên D.

Đồ thị hàm số y = cotx trên D được biểu diễn như hình sau:

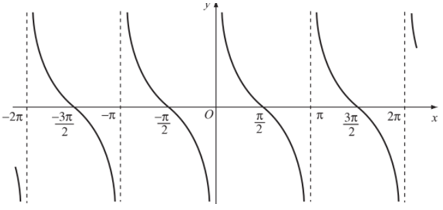
Tập giá trị của hàm số y = cotx là $\left(-\infty ;+\infty \right)$.