50 Bài tập Giới hạn của hàm số (có đáp án)- Toán 11

Bài tập Toán 11 Chương 4 Bài 2: Giới hạn của hàm số

A. Bài tập Giới hạn của hàm số

I. Bài tập trắc nghiệm

Bài 1:

A. 0 

B. -1        

C. $\frac{–1}{2}$        

D. -∞

Lời giải:

Chọn đáp án A

Bài 2:

A. $\frac{1}{4}$        

B. $\frac{1}{6}$        

C. $\frac{1}{8}$        

D. $\frac{–1}{8}$

Lời giải:

Chọn đáp án C

Bài 3:

A. +∞        

B. $\frac{1}{8}$        

C. –$\frac{9}{8}$        

D. -∞

Lời giải:

Chọn đáp án D

Bài 4: Cho hàm số

Khi đó:

A. -1        

B. 0        

C. 1        

D. +∞

Lời giải:

Chọn đáp án C

Bài 5: Cho hàm số

 . Xác định a; b để hàm số có giới hạn tại x = 3 và x = 5 .

Lời giải:

Chọn đáp án A

Bài 6: Tìm 

A. 0

B. 2

C. +∞

D. -∞

Lời giải:

Chọn đáp án A

Bài 7: Tìm 

A. $\frac{23}{3}$

B. +∞

C. –$\frac{23}{3}$

D. -∞

Lời giải:

Chọn đáp án C

Bài 8: Tìm 

A. 1

B. 2

C. 3

D.4

Lời giải:

Chọn đáp án D

Bài 9: Tính 

A. 0

B.1

C. 2

D. $3\sqrt{2}$

Lời giải:

Chọn đáp án A

Bài 10: Giá trị đúng của  là:

A. – 1

B. 1

C. 7

D. +∞

Lời giải:

Chọn đáp án B

II. Bài tập tự luận có lời giải

Bài 1:

Lời giải:

Bài 2:

Lời giải:

Bài 3:

Lời giải:

Bài 4:

Lời giải:

Chia cả tử và mẫu của phân thức cho x4 ta có

Bài 5:

Lời giải:

Bài 6:

Lời giải:

Bài 7:

Lời giải:

Bài 8:

Lời giải:

Bài 9:

Lời giải:

Bài 10:

Lời giải:

III. Bài tập vận dụng

Bài 1  bằng?

Bài 2 Giá tri đúng của ?

Bài 3 Cho hàm số . Chọn kết quả đúng của ?

Bài 4 Giới hạn của hàm số  khi x → -∞ bằng?

Bài 5 Giới hạn  bằng?

Bài 6 Giả sử . Hệ số a bằng bao nhiêu để L = 3 ?

Bài 7 Giới hạn  bằng?

Bài 8 Giới hạn  bằng?

Bài 9 Giới hạn  bằng?

Bài 10 Giới hạn  bằng?

B. Lý thuyết Giới hạn của hàm số

I. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM

 

1. Định nghĩa

Định nghĩa 1

Cho khoảng K chứa điểm x₀ và hàm số y = f(x) xác định trên K hoặc trên K \ {x₀}.

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n K \{x₀} và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to \infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$ hay f(x) → L khi x → x₀.

Nhận xét: $\underset{\mathrm{x}\to \infty }{\lim }\mathrm{x}={\mathrm{x}}_0,\underset{\mathrm{x}\to \infty }{\lim }\mathrm{c}=\mathrm{c}$ với c là hằng số.

Ví dụ 1. Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)=\frac{{\mathrm{x}}^3-8}{\mathrm{x}-2}$. Chứng minh rằng $\underset{\mathrm{x}\to 2}{\lim }\mathrm{f}\left(\mathrm{x}\right)=12.$

Giải

Hàm số xác định trên $\mathrm{ℝ}\backslash \left\{2\right\}$

Giả sử (x_n) là một dãy số bất kì, thỏa mãn ${\mathrm{x}}_{\mathrm{n}}\ne 2$ và ${\mathrm{x}}_{\mathrm{n}}\to 2$ khi $\mathrm{n}\to +\infty$.

 

Ta có:

$\text{limf}\left({\mathrm{x}}_{\mathrm{n}}\right)=\lim \frac{{\mathrm{x}}_{\mathrm{n}}^3-8}{{\mathrm{x}}_{\mathrm{n}}-2}=\lim \frac{\left({\mathrm{x}}_{\mathrm{n}}-2\right)\left({\mathrm{x}}_{\mathrm{n}}^2+2{\mathrm{x}}_{\mathrm{n}}+4\right)}{{\mathrm{x}}_{\mathrm{n}}-2}=\lim \left({\mathrm{x}}_{\mathrm{n}}^2+2{\mathrm{x}}_{\mathrm{n}}+4\right)=12.$

Vậy $\underset{\mathrm{x}\to 2}{\lim }\mathrm{f}\left(\mathrm{x}\right)=12.$

2. Định lí về giới hạn hữu hạn

Định lí 1

a) Giả sử $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$ và $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{g}\left(\mathrm{x}\right)=\mathrm{M}$. Khi đó:

$\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\left[\mathrm{f}\left(\mathrm{x}\right)+\mathrm{g}\left(\mathrm{x}\right)\right]=\mathrm{L}+\mathrm{M};\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\left[\mathrm{f}\left(\mathrm{x}\right)-\mathrm{g}\left(\mathrm{x}\right)\right]=\mathrm{L}-\mathrm{M};\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right).\mathrm{g}\left(\mathrm{x}\right)=\mathrm{L}.\mathrm{M};\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}=\frac{\mathrm{L}}{\mathrm{M}}\left(\mathrm{M}\ne 0\right);$

b) Nếu $\mathrm{f}\left(\mathrm{x}\right)\ge 0$ và $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$ thì $\mathrm{L}\ge 0$ và $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\sqrt{\mathrm{f}\left(\mathrm{x}\right)}=\sqrt{\mathrm{L}}.$

(Dấu của f(x) được xét trên khoảng đang tìm giới hạn với $\mathrm{x}\ne {\mathrm{x}}_0$).

Ví dụ 2. Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)=\frac{1-\mathrm{x}}{{\left(\mathrm{x}-4\right)}^2}$. Tính $\underset{\mathrm{x}\to 4}{\lim }\mathrm{f}\left(\mathrm{x}\right).$

Giải

Ta có:

$\underset{\mathrm{x}\to 4}{\lim }\left(1-\mathrm{x}\right)=-3<0, \underset{\mathrm{x}\to 4}{\lim }{\left(\mathrm{x}-4\right)}^2=0\Rightarrow \underset{\mathrm{x}\to 4}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 4}{\lim }\frac{1-\mathrm{x}}{{\left(\mathrm{x}-4\right)}^2}=-\infty$

3. Giới hạn một bên

Định nghĩa 2

– Cho hàm số y = f(x) xác định trên (x₀; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to {\mathrm{x}}_0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$

– Cho hàm số y = f(x) xác định trên (a; x₀).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x₀ nếu với dãy số (x_n) bất kì, a < x_n < x₀ và x_n → x₀, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to {\mathrm{x}}_0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$.

Định lí 2

$\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}\iff \underset{\mathrm{x}\to {\mathrm{x}}_0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to {\mathrm{x}}_0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$

Ví dụ 3. Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}\sqrt{\mathrm{x}}+1\text{ khi x}\ge \text{0}\\ \text{2x khi x < 0}\end{array}\right.$. Tìm $\underset{\mathrm{x}\to 0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right);\underset{\mathrm{x}\to 0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)$ và $\underset{\mathrm{x}\to 0}{\lim }\mathrm{f}\left(\mathrm{x}\right)$ (nếu có).

Giải

Ta có:  

$\underset{\mathrm{x}\to 0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 0^{+}}{\lim }\left(\sqrt{\mathrm{x}}+1\right)=0;\underset{\mathrm{x}\to 0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 0^{-}}{\lim }2\mathrm{x}=0;\Rightarrow \underset{\mathrm{x}\to 0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=0$

Do đó $\underset{\mathrm{x}\to 0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=0.$

Vậy $\underset{\mathrm{x}\to 0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=0$ và $\underset{\mathrm{x}\to 0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=0.$

II. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC

Định nghĩa 3

a) Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to +\infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$

b) Cho hàm số y = f(x) xác định trên (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (x_n) bất kì, x_n < a và x_n → –∞, ta có f(x_n) → L.

Kí hiệu: $\underset{\mathrm{x}\to -\infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{L}$

Chú ý:

a) Với c, k là hằng số và k nguyên dương, ta luôn có:

$\underset{\mathrm{x}\to +\infty }{\lim }\mathrm{c}=\mathrm{c};\underset{\mathrm{x}\to -\infty }{\lim }\mathrm{c}=\mathrm{c};$ $\underset{\mathrm{x}\to +\infty }{\lim }\frac{\mathrm{c}}{{\mathrm{x}}^{\mathrm{k}}}=0;\underset{\mathrm{x}\to -\infty }{\lim }\frac{\mathrm{c}}{{\mathrm{x}}^{\mathrm{k}}}=0.$

b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x₀ vẫn còn đúng khi x_n → +∞ hoặc x → –∞

III. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ

1. Giới hạn vô cực

Định nghĩa 4

Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → –∞

Kí hiệu: $\underset{\mathrm{x}\to \infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=-\infty$

Nhận xét:

$\underset{\mathrm{x}\to +\infty }{\lim }\mathrm{f}\left(\mathrm{x}\right)=+\infty \iff \underset{\mathrm{x}\to +\infty }{\lim }\left(-\mathrm{f}\left(\mathrm{x}\right)\right)=-\infty$.

2. Một vài giới hạn đặc biệt

a) $\underset{\mathrm{x}\to +\infty }{\lim }{\mathrm{x}}^{\mathrm{k}}=+\infty$ với k nguyên dương.

b) Nếu k chẵn thì $\underset{\mathrm{x}\to -\infty }{\lim }{\mathrm{x}}^{\mathrm{k}}=+\infty$;

Nếu k lẻ thì $\underset{\mathrm{x}\to -\infty }{\lim }{\mathrm{x}}^{\mathrm{k}}=-\infty$.

3. Một vài quy tắc về giới hạn vô cực

a) Quy tắc tìm giới hạn của tích f(x).g(x)

b) Quy tắc tìm giới hạn của thương $\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}$

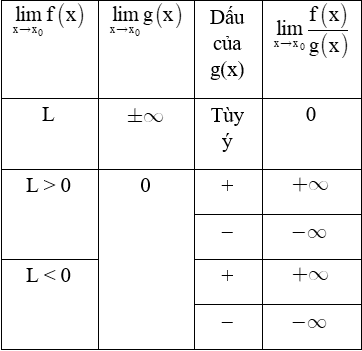
(Dấu của g(x) xét trên một khoảng K nào đó đang tính giới hạn, với $\mathrm{x}\ne {\mathrm{x}}_0$)

Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp:

$\mathrm{x}\to {\mathrm{x}}_0^{+},\mathrm{x}\to {\mathrm{x}}_0^{-};\mathrm{x}\to +\infty ;\mathrm{x}\to -\infty .$

Ví dụ 4. Tính các giới hạn sau:

a) $\underset{\mathrm{x}\to \infty }{\lim }\left({\mathrm{x}}^4-3\mathrm{x}+8\right)$;

b) $\underset{\mathrm{x}\to 1^{-}}{\lim }\frac{5\mathrm{x}-6}{2\mathrm{x}-2};$

c) $\underset{\mathrm{x}\to -3^{+}}{\lim }\frac{\mathrm{x}}{\mathrm{x}+3};$

Giải

a)

 $\underset{\mathrm{x}\to +\infty }{\lim }\left({\mathrm{x}}^4-3\mathrm{x}+8\right)=\underset{\mathrm{x}\to \infty }{\lim }{\mathrm{x}}^4\left(1-\frac{3}{{\mathrm{x}}^3}+\frac{8}{{\mathrm{x}}^4}\right)=\underset{\mathrm{x}\to +\infty }{\lim }{\mathrm{x}}^4.\underset{\mathrm{x}\to +\infty }{\lim }\left(1-\frac{3}{{\mathrm{x}}^3}+\frac{8}{{\mathrm{x}}^4}\right)=+\infty$

(Vì $\underset{\mathrm{x}\to +\infty }{\lim }{\mathrm{x}}^4=+\infty ;$$\underset{\mathrm{x}\to +\infty }{\lim }\left(1-\frac{3}{{\mathrm{x}}^3}+\frac{8}{{\mathrm{x}}^4}\right)=1$).

b)

$\underset{\mathrm{x}\to 1^{-}}{\lim }\frac{5\mathrm{x}-6}{2\mathrm{x}-2}=\underset{\mathrm{x}\to 1^{-}}{\lim }\left(5\mathrm{x}-6\right):\underset{\mathrm{x}\to 1^{-}}{\lim }\left(2\mathrm{x}-2\right)=+\infty$

(Vì $\underset{\mathrm{x}\to 1^{-}}{\lim }\left(5\mathrm{x}-6\right)=-1<0;$$\underset{\mathrm{x}\to 1^{-}}{\lim }\left(2\mathrm{x}-2\right)=0$ và 2x – 2 < 0 với mọi x < 1).

c)

$\underset{\mathrm{x}\to -3^{+}}{\lim }\frac{\mathrm{x}}{\mathrm{x}+3}=\underset{\mathrm{x}\to -3^{+}}{\lim }\mathrm{x}:\underset{\mathrm{x}\to -3^{+}}{\lim }\left(\mathrm{x}+3\right)=-\infty$

( Vì $\underset{x\to -3^{+}}{\lim }x=-3<0;$$\underset{x\to -3^{+}}{\lim }\left(x+3\right)=0$ và x + 3 > 0 với mọi x > – 3 ).