Lý thuyết Toán lớp 6 Bài 1: Phân số với tử số và mẫu số là số nguyên
Video giải Toán 6 Bài 1: Phân số với tử số và mẫu số là số nguyên – Chân trời sáng tạo
A. Lý thuyết Phân số với tử số và mẫu số là số nguyên
1. Khái niệm phân số
Ta gọi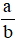 
, trong đó 
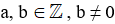là phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số. Phân số 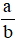đọc là a phần b.
Ví dụ 1. Phân số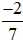 
có tử số là −2, mẫu số là 7 và được đọc là “âm hai phần bảy”.
Chú ý: Ta có thể dùng phân số để ghi (viết, biểu diễn) kết quả phép chia một số nguyên cho một số nguyên khác 0.
Ví dụ 2. Phân số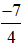 
là ghi kết quả phép chia −7 cho 4.
2. Phân số bằng nhau
Hai phân số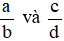 
được gọi là bằng nhau, viết là 
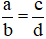, nếu a . d = b . c.
Ví dụ 3.
a)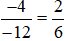 
vì (−4) . 6 = (−12) . 2 (cùng bằng –24).
b) 
không bằng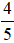 
, vì 3 . 5 không bằng 4 . 4. Viết 
.
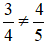Chú ý: Điều kiện a . d = b . c gọi là điều kiện bằng nhau của hai phân số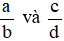
Ví dụ 4. Các cặp phân số sau có bằng nhau hay không?
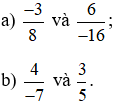
Lời giải:
a)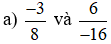 
So sánh hai tích: (−3) . (−16) và 8 . 6;
Ta có: (−3) . (−16) = 3 . 16 = 48 và 8 . 6 = 48.
Nên (−3) . (−16) = 8 . 6. Do đó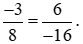 
.
.
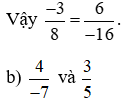So sánh hai tích: 4 . 5 và (−7) . 3;
Ta có: 4 . 5 = 20 và (−7) . 3 = −21.
Nên 4 . 5 ≠ (−7) . 3. Do đó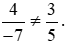 
.
Vậy hai phân số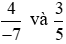 
không bằng nhau.
3. Biểu diễn số nguyên ở dạng phân số
Mỗi số nguyên n có thể coi là phân số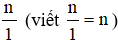 
. Khi đó số nguyên n được biểu diễn ở dạng phân số 
.
Ví dụ 5.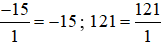 
.
B. Bài tập tự luyện
Bài 1. Đọc các phân số sau:
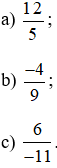
Lời giải:
a) Phân số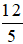 
có tử số là 12, mẫu số là 5.
Đọc là: Mười hai phần năm;
b) Phân số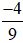 
có tử số là −4, mẫu số là 9.
Đọc là: Âm bốn phần chín;
c) Phân số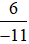 
có tử số là 6, mẫu số là −11.
Đọc là: Sáu phần âm mười một.
Bài 2. Vẽ lại hình bên và tô màu để phân số biểu thị phần tô màu bằng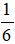 
.
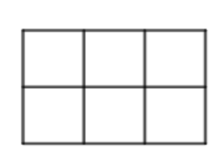
Lời giải:
Phân số 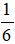có tử số là 1, mẫu số là 6.
Phân số biểu thị phần tô màu bằng 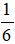tức là hình đó được chia thành 6 phần bằng nhau và tô màu 1 phần.
Ta có hình vẽ biểu thị phần tô màu bằng 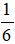như sau:
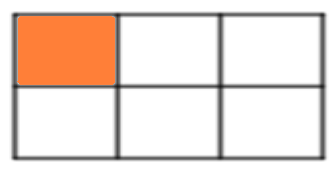
Bài 3. Tìm cặp phân số bằng nhau trong các cặp phân số sau:
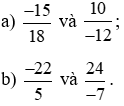
Lời giải:
a)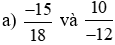 
So sánh hai tích: (−15) . (−12) và 18 . 10;
Ta có: (−15) . (−12) = 15 . 12 = 180 và 18 . 10 = 180.
Nên (−15) . (−12) = 18 . 10.
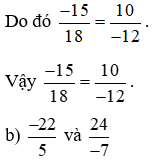
So sánh hai tích: (−22) . (−7) và 5 . 24;
Ta có: (−22) . (−7) = 22 . 7 = 154 và 5 . 24 = 120.
Nên (−22) . (−7) ≠ 5 . 24.
Do đó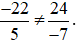 
.
Vậy hai phân số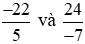 
không bằng nhau.
Bài 4. Một bể bơi có máy bơm A để bơm nước vào bể. Nếu bể không có nước máy bơm sẽ bơm đầy bể trong 11 giờ. Cũng bể bơi đó, có máy bơm B dùng để tháo nước ra khỏi bể khi vệ sinh bể bơi. Nếu bể đầy nước, máy bơm B sẽ bơm hết nước trong bể chỉ trong 7 giờ.
Điền phân số với tử và mẫu là số nguyên thích hợp vào bảng sau đây:
Lời giải:
– Máy bơm A sẽ bơm từ khi chưa có nước đến khi đầy bể mất 11 giờ nên phân số ở mỗi ô có mẫu số là 11, tử số là số giờ bơm tương ứng.
– Máy bơm B sẽ tháo nước từ khi đầy bể đến khi hết sạch nước trong bể là 7 giờ nên phân số ở mỗi ô có mẫu số là 7, tử số là số âm của giờ bơm tương ứng.
Ta có bảng sau:
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Chương 4: Một số yếu tố thống kê
Bài 2: Tính chất cơ bản của phân số
Bài 3: So sánh phân số
Bài 4: Phép cộng và phép trừ phân số
Bài 5: Phép nhân và phép chia phân số
====== ****&**** =====