Sách bài tập Toán 10 Bài 1 (Chân trời sáng tạo): Giá trị lượng giác của một góc từ 0 đến 180

Giải SBT Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180

Giải SBT Toán 10 trang 69 Tập 1

Bài 1 trang 69 SBT Toán 10 Tập 1: Tính giá trị của T = 4cos60° + 2sin135° + 3cot120°.

Lời giải

Sử dụng máy tính cầm tay ta có:

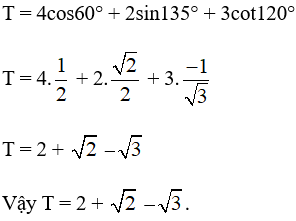
Bài 2 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng:

a) sin138° = sin42°;                                                                 

b) tan125° = – cot35°.

Lời giải

a) Ta có sinx = sin(180° – x ) nên:

sin138° = sin (180° – 138°) = sin42°.

Vậy sin138° = sin42°.

b) Ta có tanx = –tan(180° – x ) và tanx = cot( 90° – x )

tan125 = –tan(180° – 125° ) = –tan55° = –cot( 90° – 55° ) = –cot35°.

Vậy tan125° = – cot35°.

Bài 3 trang 69 SBT Toán 10 Tập 1: Tìm góc α ( 0° ≤ α ≤ 180° ) trong mỗi trường hợp sau:

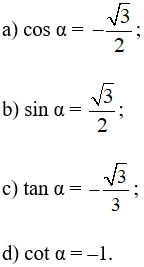
ý b

ý c

ý d

Lời giải

a) Sử dụng máy tính cầm tay, ta có được: α = 150°.

b) Sử dụng máy tính cầm tay, ta có được: α = 60°.

Lại có sinα = sin(180° – α ) nên α = 120°.

Vậy α = 60° hoặc α = 120°.

c) Dựa vào bảng các giá trị lượng giác đặc biệt, ta có: tan α = $-\frac{\sqrt{3}}{3}$ ⇒ α = 150°.

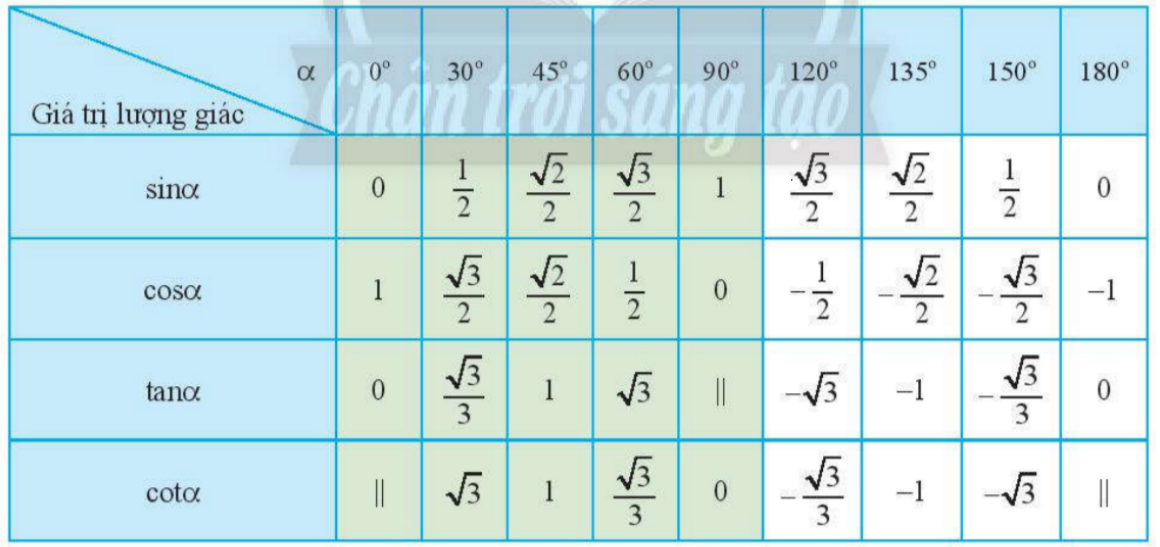
d) Dựa vào bảng các giá trị lượng giác đặc biệt, ta có: cot α = –1 ⇒ α = 135°.

Vậy α = 135°.

Bài 4 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng trong tam giác ABC ta có:

a) tanB = –tan( A+C);                                                   

b) sinC = sin ( A+B ).

Lời giải

a) Trong tam giác ABC có: $\widehat{\text{A}}+\widehat{\text{B}}+\widehat{\text{C}}$ = 180° ⇒ $\widehat{\text{A}}+\widehat{\text{C}}$= 180° – $\widehat{\text{B}}$

Ta có: tanα = –tan(180° – α ) nên

tanB = –tan( 180° – B ) = –tan( A+C)

Vậy tanB = –tan( A+C).

b) Trong tam giác ABC có: $\widehat{\text{A}}+\widehat{\text{B}}+\widehat{\text{C}}$= 180° ⇒$\widehat{\text{A}}+\widehat{\text{B}}$= 180° – $\widehat{\text{C}}$.

Ta có: sinα = sin(180° – α ) nên

sinC = sin(180° – C ) = sin ( A+B ).

Vậy sinC = sin ( A+B ).

Bài 5 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng với mọi góc x ( 0° ≤ x ≤ 90°), ta đều có:

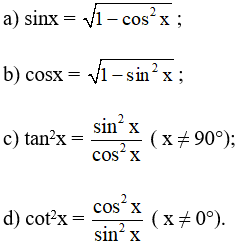
ý b

ý c 

ý d

Lời giải

a) Ta có: ${\text{cos}}^{\text{2}}{\text{x\hspace{0.17em}+\hspace{0.17em}sin}}^{\text{2}}\text{x=1}$.

⇒ sin²x = 1 – cos²x

⇒ sinx = $\sqrt{1-{\cos }^2\text{x}}$ hoặc sinx = $–\sqrt{1-{\cos }^2\text{x}}$ 

Vì 0° ≤ x ≤ 90° nên 0 ≤ sinx ≤ 1. Do đó chỉ có sinx = $\sqrt{1-{\cos }^2\text{x}}$ là thỏa mãn.

Vậy sinx = $\sqrt{1-{\cos }^2\text{x}}$.

b) Ta có: cos²x + sin²x = 1

⇒ cos²x = 1 – sin²x.

⇒ cosx = $\sqrt{1-{\sin }^2\text{x}}$ hoặc cosx = $–\sqrt{1-{\sin }^2\text{x}}$ 

Vì 0° ≤ x ≤ 90° nên 0 ≤ cos ≤ 1. Do đó chỉ có cosx = $\sqrt{1-{\sin }^2\text{x}}$ là thỏa mãn.

Vậy cosx = $\sqrt{1-{\sin }^2\text{x}}$.

c) Ta có: tanx = $\frac{\sin \text{x}}{\cos \text{x}}$ ⇒ tan²x = $\frac{{\sin }^2\text{x}}{{\cos }^2\text{x}}$( x ≠ 90°). (ĐPCM)

d) Ta có: cotx = $\frac{\cos \text{x}}{\sin \text{x}}$ ⇒ cot²x = $\frac{{\cos }^2\text{x}}{{\sin }^2\text{x}}$ ( x ≠ 0°). (ĐPCM)

Bài 6 trang 69 SBT Toán 10 Tập 1: Cho góc x với cosx = $\frac{–1}{2}$. Tính giá trị biểu thức

S = 4sin²x + 8tan²x.

Lời giải

Sử dụng máy tính cầm tay, ta có: cosx = $\frac{–1}{2}$ ⇒ x = 120° ⇒ sinx = $\frac{\sqrt{3}}{2}$ và tanx = $-\sqrt{3}$.

S = 4sin²x + 8tan²x = 4. ${\left(\frac{\sqrt{3}}{2}\right)}^2$+ 8. ${(-\sqrt{3})}^2$ = 4.$\frac{3}{4}$ + 8.3 = 27.

Vậy S = 27.

Bài 7 trang 69 SBT Toán 10 Tập 1: Dùng máy tính cầm tay, tính.

a) sin138°12’24’’;                   

b) cos144°35’12’’;                  

c) tan152°35’44’’.

Lời giải

Sử dụng máy tính cầm tay, ta tính được:

a) sin138°12’24’’ ≈ 0,666.

b) cos144°35’12’’≈ –0,815.

c) tan152°35’44’’ ≈ –0,518.

Bài 8 trang 69 SBT Toán 10 Tập 1: Dùng máy tính cầm tay, tìm x, biết:

a) cosx = –0,234;                    

b) sinx = 0,812;                       

c) cotx = –0,333.

Lời giải

Sử dụng máy tính cầm tay, ta tính được:

a) cosx = –0,234 ⇒ x ≈ 103°31’58’’.

b) sinx = 0,812 ⇒ x ≈ 54°17’30’’ hay x ≈ 125°42’30’’.

c) cotx = –0,333 ⇒ x ≈ 108°25’4’’.

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 2: Định lí côsin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế

Bài tập cuối chương 4

====== ****&**** =====