Câu hỏi:
Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP.
Trả lời:
Lời giải
Áp dụng định lí côsin:
NP2 = MP2 + MN2 – 2.MN.MP.cos\(\widehat {\rm{M}}\)
NP2 = 102 + 202 – 2.10.20.cos42°
NP = \(\sqrt {{{10}^2} + {\rm{ }}{{20}^2}–{\rm{ }}2.10.20.{\rm{cos}}42^\circ } \)
NP ≈ 14,24.
Áp dụng định lí sin trong tam giác MNP, ta có: R = ON = OP = \(\frac{{{\rm{NP}}}}{{{\rm{2sin}}\widehat {\rm{M}}}}\) ≈ \(\frac{{14,24}}{{2\sin 42^\circ }}\) ≈ 10,64
Xét đường tròn tâm O ngoại tiếp tam giác MNP:
\(\widehat {{\rm{NMP}}}\) là góc nội tiếp chắn cung NP ⇒ \(\widehat {{\rm{NMP}}}\) = \(\frac{1}{2}\)\(\widehat {{\rm{NOP}}}\) ⇒ \(\widehat {{\rm{NOP}}}\) = 42°.2 = 84°.
Suy ra SONP = \(\frac{1}{2}\).ON.OP.sin\(\widehat {{\rm{NOP}}}\) ≈ \(\frac{1}{2}\).(10,64)2.sin84° ≈ 56,30 (đvdt)
Vậy diện tích tam giác ONP là 56,30 đvdt.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính độ dài các cạnh chưa biết trong tam giác sau:
Câu hỏi:
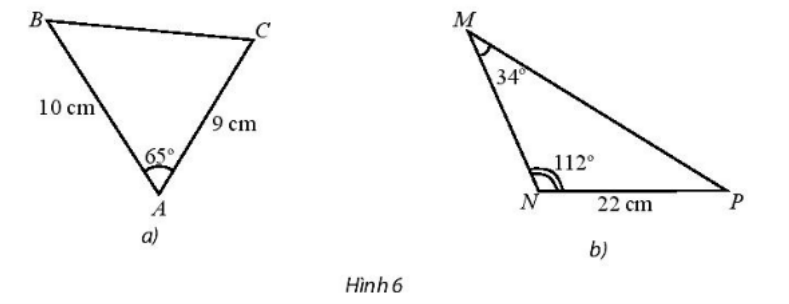
Tính độ dài các cạnh chưa biết trong tam giác sau:
Trả lời:
Lời giải
a) Áp dụng định lí côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos\(\widehat {\rm{A}}\)
BC2 = 102 + 92 – 2.10.9.cos65°
BC 2 ≈ 104,929
BC ≈ 10,24 (cm).
Vậy BC ≈ 10,24 (cm).
b) \(\widehat {\rm{P}}\)= 180° – 112° – 34° = 34°.
Ta có: \(\widehat {\rm{P}}\) = \(\widehat {\rm{M}}\) ⇒ tam giác MNP cân tại N ⇒ MN = NP = 22 (cm)
Áp dụng định lí sin ta có: \(\frac{{{\rm{MP}}}}{{{\rm{sinN}}}}{\rm{ = }}\frac{{{\rm{MN}}}}{{{\rm{sinP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{sinM}}}} = \frac{{22}}{{\sin 34^\circ }}\).
⇒ MP = \(\frac{{22}}{{\sin 34^\circ }}\).sin112° ≈ 36,48 (cm)
Vậy MP ≈ 36,48 cm, MN = 22 cm.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC biết cạnh a = 75 cm, \(\widehat {\rm{B}}\) = 80°, \(\widehat {\rm{C}}\)= 40°.
Tính các góc, các cạnh còn lại của tam giác ABC.
Câu hỏi:
Cho tam giác ABC biết cạnh a = 75 cm, \(\widehat {\rm{B}}\) = 80°, \(\widehat {\rm{C}}\)= 40°.
Tính các góc, các cạnh còn lại của tam giác ABC.Trả lời:
Lời giải
Ta có: \(\widehat {\rm{A}}\)= 180° – 80° – 40° = 60°.
Áp dụng định lí sin ta có:
\(\frac{{\rm{a}}}{{{\rm{sinA}}}}{\rm{ = }}\frac{{\rm{b}}}{{{\rm{sinB}}}}{\rm{ = }}\frac{{\rm{c}}}{{{\rm{sinC}}}}\) = \(\frac{{75}}{{\sin 60^\circ }}\)
⇒ b = \(\frac{{75}}{{\sin 60^\circ }}\). sin80° ≈ 85,29 (cm);
⇒ c = \(\frac{{75}}{{\sin 60^\circ }}\). sin40° ≈ 55,67 (cm).
Vậy AC ≈ 85,29 cm; AB ≈ 55,67 cm và \(\widehat {\rm{A}}\)= 60°.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Câu hỏi:
Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Trả lời:
Lời giải
R = \(\frac{{\rm{a}}}{{{\rm{2sinA}}}}\) = \(\frac{{75}}{{2.\sin 60^\circ }}\) = 25\(\sqrt 3 \) (cm).
Vậy R = 25\(\sqrt 3 \) cm.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm góc lớn nhất của tam giác ABC, biết a = 8, b = 12, c = 6.
Câu hỏi:
Tìm góc lớn nhất của tam giác ABC, biết a = 8, b = 12, c = 6.
Trả lời:
Lời giải
Do b là cạnh lớn nhất nên B là góc lớn nhất.
Theo định lí côsin: b2 = a2 + c2 – 2accosB
⇒ cosB = \(\frac{{{{\rm{a}}^2} + {{\rm{c}}^2} – {{\rm{b}}^2}}}{{2{\rm{ac}}}}\) = \(\frac{{{8^2} + {6^2} – {{12}^2}}}{{2.8.6}}\)
⇒ cosB = \(\frac{{ – 11}}{{24}}\).
⇒ \(\widehat {\rm{B}}\) = 117°16’46’’.
Vậy góc lớn nhất của tam giác ABC là \(\widehat {\rm{B}}\) = 117°16’46’’.====== **** mời các bạn xem câu tiếp bên dưới **** =====
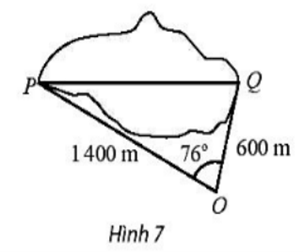
- Tính khoảng cách giữa hai điểm P và Q của một hồ nước ( Hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400m và 600m người quan sát nhìn thấy một góc 76°.
Câu hỏi:
Tính khoảng cách giữa hai điểm P và Q của một hồ nước ( Hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400m và 600m người quan sát nhìn thấy một góc 76°.
Trả lời:
Lời giải
Áp dụng định lí côsin:
PQ2 = OP2 + OQ2 – 2.OP.OQ.cos\(\widehat {\rm{O}}\)
PQ2 = 14002 + 6002 – 2.1400.600.cos76°
PQ = \(\sqrt {{{1400}^2} + {{600}^2}–{\rm{ }}2.1400.600.{\rm{cos}}76^\circ } \)
PQ ≈ 1383,32 (m).
Vậy khoảng cách giữa hai điểm PQ là PQ ≈ 1383,32 (m).====== **** mời các bạn xem câu tiếp bên dưới **** =====