Câu hỏi:
Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
BC = 10, AC = 20, \(\widehat {\rm{C}}\) = 80°;
Trả lời:
Lời giải
Áp dụng định lí côsin ta có:
AB2 = BC2 + AC2 – 2BC.AC.cos\(\widehat {\rm{C}}\)
AB2 = 102 + 202 – 2.10.20.cos80°
AB = \(\sqrt {{{10}^2} + {\rm{ }}{{20}^2}–{\rm{ }}2.10.20.{\rm{cos}}80^\circ } \)
AB ≈ 20,75.
Áp dụng định lí sin ta có: \(\frac{{{\rm{AB}}}}{{{\rm{sinC}}}}{\rm{ = }}\frac{{{\rm{AC}}}}{{{\rm{sinB}}}}{\rm{ = }}\frac{{{\rm{BC}}}}{{{\rm{sinA}}}}\)≈ \(\frac{{20,75}}{{\sin 80^\circ }}\).
⇒ sinB = AC : \(\frac{{20,75}}{{\sin 80^\circ }}\) = 20 : \(\frac{{20,75}}{{\sin 80^\circ }}\) ≈ 0,949 ⇒ \(\widehat {\rm{B}}\) ≈ 71°37’.
⇒ sinA = BC : \(\frac{{20,75}}{{\sin 80^\circ }}\) = 10 : \(\frac{{20,75}}{{\sin 80^\circ }}\) ≈ 0,475 ⇒ \(\widehat {\rm{C}}\) ≈ 28°21’.
Vậy \(\widehat {\rm{B}}\) ≈ 71°37’ và \(\widehat {\rm{C}}\) ≈ 28°21’.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có BC = a, AC = b, AB = c và
a = b. Chứng minh rằng: c2 = 2a2 (1 – cosC ).
Câu hỏi:
Cho tam giác ABC có BC = a, AC = b, AB = c và
a = b. Chứng minh rằng: c2 = 2a2 (1 – cosC ).Trả lời:
Lời giải
Áp dụng định lí côsin ta có:
c2 = a2 + b2 – 2abcosC
mà a = b nên
c2 = a2 + a2 – 2a2cosC
c2 = 2a2 – 2a2cosC
c2 = 2a2 (1 – cosC ).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
\(\widehat {\rm{A}}\) = 42°, \(\widehat {\rm{B}}\) = 63°;
Câu hỏi:
Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
\(\widehat {\rm{A}}\) = 42°, \(\widehat {\rm{B}}\) = 63°;Trả lời:
Lời giải
Tam giác ABC có: \(\widehat {\rm{A}}\) + \(\widehat {\rm{B}}\) + \(\widehat {\rm{C}}\) = 180°.
⇒ \(\widehat {\rm{C}}\) = 180° – \(\widehat {\rm{A}}\)– \(\widehat {\rm{B}}\) = 180° – 42° – 63° = 75°.
Vậy \(\widehat {\rm{C}}\) = 75°.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
AB = 15, AC = 25, BC = 30.
Câu hỏi:
Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
AB = 15, AC = 25, BC = 30.Trả lời:
Lời giải
Theo định lí côsin ta có: AB2 = BC2 + AC2 – 2BC.AC.cos\(\widehat {\rm{C}}\)
⇒ cos\(\widehat {\rm{C}}\) = \(\frac{{{\rm{B}}{{\rm{C}}^2} + {\rm{A}}{{\rm{C}}^2} – {\rm{A}}{{\rm{B}}^2}}}{{2.{\rm{BC}}.{\rm{AC}}}}\) = \(\frac{{{{30}^2} + {{25}^2} – {{15}^2}}}{{2.30.25}}\) = \(\frac{{13}}{{15}}\) ⇒ \(\widehat {\rm{C}}\) ≈ 29°55’.
Tương tự như trên, ta có:
cos\(\widehat {\rm{A}}\) = \(\frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} – {\rm{BC}}{^2}}}{{2.{\rm{AB}}.{\rm{AC}}}}\)= \(\frac{{{{15}^2} + {{25}^2} – {{30}^2}}}{{2.15.25}}\) = \(\frac{{ – 1}}{{15}}\) ⇒ \(\widehat {\rm{A}}\) ≈ 93°49’.
cos\(\widehat {\rm{B}}\) = \(\frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^2} – {\rm{AC}}{^2}}}{{2.{\rm{AB}}.{\rm{BC}}}}\)= \(\frac{{{{15}^2} + {{30}^2} – {{25}^2}}}{{2.15.30}}\) = \(\frac{5}{9}\) ⇒ \(\widehat {\rm{B}}\) ≈ 56°15’.====== **** mời các bạn xem câu tiếp bên dưới **** =====
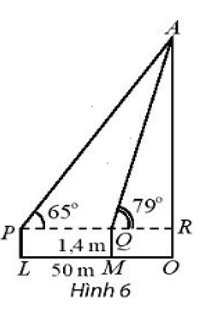
- Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RQA}}}\)= 79°, người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RPA}}}\)= 65°. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m ( Hình 6).
Câu hỏi:
Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RQA}}}\)= 79°, người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RPA}}}\)= 65°. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m ( Hình 6).
Trả lời:
Lời giải
Đặt d = PQ = 50m; h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
Ta có: \(\widehat {{\rm{RQA}}}\)= 79° và \(\widehat {{\rm{RPA}}}\)= 65°
tan\(\widehat {{\rm{RQA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{QR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{QR}}}}\) ⇒ QR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RQA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\).
tan\(\widehat {{\rm{RPA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{PR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{PR}}}}\) ⇒ PR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RPA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\).
Ta có:
PQ = PR – QR = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\) – \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\) = h \(\left( {\frac{1}{{\tan 65^\circ }} – \frac{1}{{\tan 79^\circ }}} \right)\) = 50 (m)
⇒ h ≈ 183,9 (m)
Vậy chiều cao của tòa nhà là AR + RO ≈ 183,9 + 1,4 = 185,3 (m).====== **** mời các bạn xem câu tiếp bên dưới **** =====
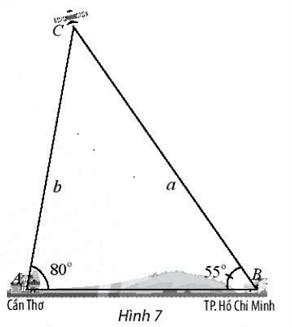
- Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát ở hai thành phố Hồ Chí Minh và Cần Thơ. Khi vệ tinh nằm giữa hai trạm này, góc nâng của nó được quan sát đồng thời là 55° tại Thành phố Hồ Chí Minh và 80° tại Cần Thơ. Hỏi khi đó vệ tinh cách trạm quan sát Cần Thơ bao xa? Biết rằng, khoảng cách giữa hai trạm quan sát là 127km.
Câu hỏi:
Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát ở hai thành phố Hồ Chí Minh và Cần Thơ. Khi vệ tinh nằm giữa hai trạm này, góc nâng của nó được quan sát đồng thời là 55° tại Thành phố Hồ Chí Minh và 80° tại Cần Thơ. Hỏi khi đó vệ tinh cách trạm quan sát Cần Thơ bao xa? Biết rằng, khoảng cách giữa hai trạm quan sát là 127km.
Trả lời:
Lời giải
Tam giác ABC có: \(\widehat {\rm{A}}\) + \(\widehat {\rm{B}}\) + \(\widehat {\rm{C}}\) = 180°.
⇒ \(\widehat {\rm{C}}\) = 180° – \(\widehat {\rm{A}}\)– \(\widehat {\rm{B}}\) = 180° – 80° – 55° = 45°.
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{{\rm{AB}}}}{{{\rm{sinC}}}} = \frac{{{\rm{AC}}}}{{{\rm{sinB}}}}\) ⇒ AC = \(\frac{{{\rm{AB}}}}{{{\rm{sinC}}}}\).sinB = \(\frac{{127}}{{\sin 45^\circ }}\).sin55° ≈ 147 (km).
Vậy khoảng cách giữa trạm Cần Thơ và vệ tinh khoảng 147 km.====== **** mời các bạn xem câu tiếp bên dưới **** =====