Tính khoảng cách AB giữa nóc hai tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 360 km, 340 km và góc nhìn từ vệ tinh đến A và B là là 13,2° ( Hình 8).

Câu hỏi:

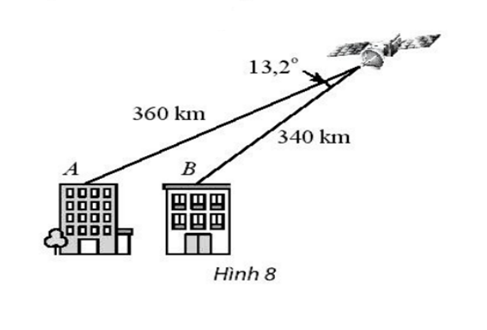
Tính khoảng cách AB giữa nóc hai tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 360 km, 340 km và góc nhìn từ vệ tinh đến A và B là là 13,2° ( Hình 8).

Trả lời:

Lời giải
Gọi điểm O đại diện cho vệ tinh.
Áp dụng định lí côsin trong tam giác OAB:
AB² = OA² + OB² – 2.OA.OB.cos\(\widehat {\rm{O}}\)
AB² = 360² + 340² – 2.360.340.cos13,2°
AB = \(\sqrt {{{360}^2} + {\rm{ }}{{340}^2}–{\rm{ }}2.360.340.{\rm{cos}}13,2^\circ } \)
AB ≈ 82,87 km.
Vậy khoảng cách giữa hai nóc nhà tòa cao ốc khoảng 82,87 km.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tam giác ABC có BC = a, AC = b, AB = c và a = b. Chứng minh rằng: c2 = 2a2 (1 – cosC ).
   
   

   Câu hỏi:
   

   Cho tam giác ABC có BC = a, AC = b, AB = c và
   a = b. Chứng minh rằng: c² = 2a² (1 – cosC ).

   Trả lời:

   Lời giải
   Áp dụng định lí côsin ta có:                          
   c² = a² + b² – 2abcosC
   mà a = b nên
   c² = a² + a² – 2a²cosC
   c² = 2a² – 2a²cosC
   c² = 2a² (1 – cosC ).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tính các góc chưa biết của tam giác ABC trong các trường hợp sau: \(\widehat {\rm{A}}\) = 42°, \(\widehat {\rm{B}}\) = 63°;
   
   

   Câu hỏi:
   

   Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
   \(\widehat {\rm{A}}\) = 42°, \(\widehat {\rm{B}}\) = 63°;

   Trả lời:

   Lời giải
   Tam giác ABC có: \(\widehat {\rm{A}}\) + \(\widehat {\rm{B}}\) + \(\widehat {\rm{C}}\) = 180°.
   ⇒ \(\widehat {\rm{C}}\) = 180° – \(\widehat {\rm{A}}\)– \(\widehat {\rm{B}}\) = 180° – 42° – 63° = 75°.
   Vậy \(\widehat {\rm{C}}\) = 75°.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tính các góc chưa biết của tam giác ABC trong các trường hợp sau: BC = 10, AC = 20, \(\widehat {\rm{C}}\) = 80°;
   
   

   Câu hỏi:
   

   Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
   BC = 10, AC = 20, \(\widehat {\rm{C}}\) = 80°;

   Trả lời:

   Lời giải
   Áp dụng định lí côsin ta có:
   AB² = BC² + AC² – 2BC.AC.cos\(\widehat {\rm{C}}\)
   AB² = 10² + 20² – 2.10.20.cos80°
   AB = \(\sqrt {{{10}^2} + {\rm{ }}{{20}^2}–{\rm{ }}2.10.20.{\rm{cos}}80^\circ } \)
   AB ≈ 20,75.
   Áp dụng định lí sin ta có: \(\frac{{{\rm{AB}}}}{{{\rm{sinC}}}}{\rm{ = }}\frac{{{\rm{AC}}}}{{{\rm{sinB}}}}{\rm{ = }}\frac{{{\rm{BC}}}}{{{\rm{sinA}}}}\)≈ \(\frac{{20,75}}{{\sin 80^\circ }}\).
   ⇒ sinB = AC : \(\frac{{20,75}}{{\sin 80^\circ }}\) = 20 : \(\frac{{20,75}}{{\sin 80^\circ }}\) ≈ 0,949 ⇒ \(\widehat {\rm{B}}\) ≈ 71°37’.
   ⇒ sinA = BC : \(\frac{{20,75}}{{\sin 80^\circ }}\) = 10 : \(\frac{{20,75}}{{\sin 80^\circ }}\) ≈ 0,475 ⇒ \(\widehat {\rm{C}}\) ≈ 28°21’.
   Vậy \(\widehat {\rm{B}}\) ≈ 71°37’ và \(\widehat {\rm{C}}\) ≈ 28°21’.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tính các góc chưa biết của tam giác ABC trong các trường hợp sau: AB = 15, AC = 25, BC = 30.
   
   

   Câu hỏi:
   

   Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
   AB = 15, AC = 25, BC = 30.

   Trả lời:

   Lời giải

   Theo định lí côsin ta có: AB² = BC² + AC² – 2BC.AC.cos\(\widehat {\rm{C}}\)
   ⇒ cos\(\widehat {\rm{C}}\) = \(\frac{{{\rm{B}}{{\rm{C}}^2} + {\rm{A}}{{\rm{C}}^2} – {\rm{A}}{{\rm{B}}^2}}}{{2.{\rm{BC}}.{\rm{AC}}}}\) = \(\frac{{{{30}^2} + {{25}^2} – {{15}^2}}}{{2.30.25}}\) = \(\frac{{13}}{{15}}\) ⇒ \(\widehat {\rm{C}}\) ≈ 29°55’.
   Tương tự như trên, ta có:
   cos\(\widehat {\rm{A}}\) = \(\frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} – {\rm{BC}}{^2}}}{{2.{\rm{AB}}.{\rm{AC}}}}\)= \(\frac{{{{15}^2} + {{25}^2} – {{30}^2}}}{{2.15.25}}\) = \(\frac{{ – 1}}{{15}}\) ⇒ \(\widehat {\rm{A}}\) ≈ 93°49’.
   cos\(\widehat {\rm{B}}\) = \(\frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^2} – {\rm{AC}}{^2}}}{{2.{\rm{AB}}.{\rm{BC}}}}\)= \(\frac{{{{15}^2} + {{30}^2} – {{25}^2}}}{{2.15.30}}\) = \(\frac{5}{9}\) ⇒ \(\widehat {\rm{B}}\) ≈ 56°15’.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
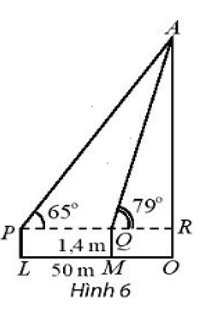
5. Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RQA}}}\)= 79°, người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RPA}}}\)= 65°. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m ( Hình 6).
   
   

   Câu hỏi:
   

   Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RQA}}}\)= 79°, người đó lùi ra xa một khoảng cách LM = 50m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {{\rm{RPA}}}\)= 65°. Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là PL = QM = 1,4 m ( Hình 6).
   

   Trả lời:

   Lời giải
   Đặt d = PQ = 50m; h = AR là chiều cao từ giác kế đến đỉnh tòa nhà.
   Ta có: \(\widehat {{\rm{RQA}}}\)= 79° và \(\widehat {{\rm{RPA}}}\)= 65°
   tan\(\widehat {{\rm{RQA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{QR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{QR}}}}\) ⇒ QR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RQA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\).
   tan\(\widehat {{\rm{RPA}}}\) = \(\frac{{{\rm{AR}}}}{{{\rm{PR}}}}\) = \(\frac{{\rm{h}}}{{{\rm{PR}}}}\) ⇒ PR = \(\frac{{\rm{h}}}{{{\rm{tan}}\widehat {{\rm{RPA}}}}}\) = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\).
   Ta có:
   PQ = PR – QR = \(\frac{{\rm{h}}}{{{\rm{tan65^\circ }}}}\) – \(\frac{{\rm{h}}}{{{\rm{tan79^\circ }}}}\) = h \(\left( {\frac{1}{{\tan 65^\circ }} – \frac{1}{{\tan 79^\circ }}} \right)\) = 50 (m)
   ⇒ h ≈ 183,9 (m)  
   Vậy chiều cao của tòa nhà là AR + RO ≈ 183,9 + 1,4 = 185,3 (m).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====