Cho hình vuông ABCD có tâm O và có cạnh bằng a. Cho hai điểm M, N thỏa mãn: MA→+MD→=0→ ; NB→+ND→+NC→=0→. Tìm độ dài các vectơ MA→, NO→.

Câu hỏi:

Cho hình vuông ABCD có tâm O và có cạnh bằng a. Cho hai điểm M, N thỏa mãn: $\overrightarrow{\text{MA}}+\overrightarrow{\text{MD}}=\overrightarrow{0}$ ; $\overrightarrow{\text{NB}}+\overrightarrow{\text{ND}}+\overrightarrow{\text{NC}}=\overrightarrow{0}$.
Tìm độ dài các vectơ $\overrightarrow{\text{MA}}$, $\overrightarrow{NO}$.

Trả lời:

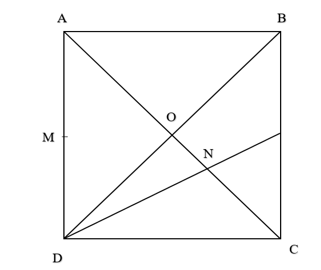
Ta có: $\overrightarrow{\text{MA}}+\overrightarrow{\text{MD}}=\overrightarrow{0}$ suy ra M là trung điểm AD. Khi đó $\left|\overrightarrow{\text{MA}}\right|$= MA = $\frac{1}{2}$AD = $\frac{a}{2}$.
Và $\overrightarrow{\text{NB}}+\overrightarrow{\text{ND}}+\overrightarrow{\text{NC}}=\overrightarrow{0}$ suy ra N là trọng tâm tam giác BCD. Khi đó $\left|\overrightarrow{NO}\right|$ = NO = $\frac{1}{3}$CO = $\frac{1}{6}$CA.
Xét hình vuông ABCD, có: CA = $=\sqrt{A{B}^2+A{C}^2}=\sqrt{{\text{a}}^2+{\text{a}}^2} =a\sqrt{2}$ 
Suy ra $\left|\overrightarrow{\text{NO}}\right|=\frac{1}{6}CA=\frac{1}{6}.a\sqrt{2}=\frac{\text{a}\sqrt{2}}{6}$.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình thoi ABCD và M là trung điểm cạnh AB, N là trung điểm cạnh CD. Chứng minh rằng: MA→ + MC→=MB→ +MD→ = MN→
   
   

   Câu hỏi:
   

   Cho hình thoi ABCD và M là trung điểm cạnh AB, N là trung điểm cạnh CD. Chứng minh rằng:
   $\overrightarrow{\text{MA}} + \overrightarrow{\text{MC}}=\overrightarrow{\text{MB}} +\overrightarrow{\text{MD}} = \overrightarrow{\text{MN}}$

   Trả lời:

   

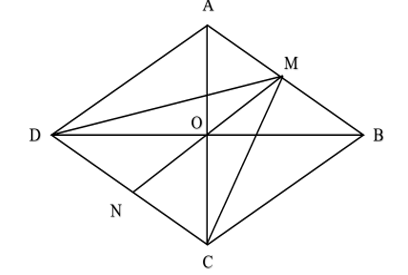
   Gọi O là tâm hình thoi. O là trung điểm của AC và BD ( tính chất hình thoi).
   ⇒ $\overrightarrow{\text{OA}} + \overrightarrow{\text{OC}} = \overrightarrow{\text{0}} và \overrightarrow{OB}+ \overrightarrow{\text{OD}}= \overrightarrow{\text{0}}$
   Ta có:
   $\overrightarrow{\text{MA}}+ \overrightarrow{\text{MC}}=\overrightarrow{\text{MO}}+\overrightarrow{OA}+ \overrightarrow{\text{MO}}+ \overrightarrow{OC}=2\overrightarrow{\text{MO}}+ \overrightarrow{OA}+ \overrightarrow{OC}=2\overrightarrow{\text{MO}}= \overrightarrow{\text{MN}}.$
   $\overrightarrow{\text{MB}}+ \overrightarrow{\text{MD}}=\overrightarrow{\text{MO}}+\overrightarrow{OB}+ \overrightarrow{\text{MO}}+ \overrightarrow{OD}=2\overrightarrow{\text{MO}}+ \overrightarrow{OB}+ \overrightarrow{OD}=2\overrightarrow{\text{MO}}= \overrightarrow{\text{MN}}.$
   Vậy $\overrightarrow{\text{MA}} + \overrightarrow{\text{MC}}= \overrightarrow{\text{MB}}+ \overrightarrow{\text{MD}}=\overrightarrow{\text{MN}}$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có: a) AB→+BC→+CD→+DA→=0→.
   
   

   Câu hỏi:
   

   Chứng minh rằng với tứ giác ABCD bất kì, ta luôn có:
   a) $\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}+\overrightarrow{\text{CD}}+\overrightarrow{\text{DA}}=\overrightarrow{0}$.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) AB→−AD→=CB→−CD→
   
   

   Câu hỏi:
   

   b) $\overrightarrow{\text{AB}}-\overrightarrow{\text{AD}}=\overrightarrow{\text{CB}}-\overrightarrow{\text{CD}}$

   Trả lời:

   

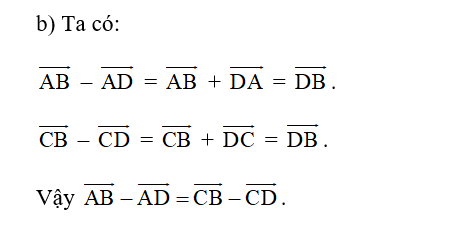
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ AB→+BC→ và AB→−BC→​.
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ $\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}$ và $\overrightarrow{\text{AB}}-\overrightarrow{\text{BC}}\text{}$.

   Trả lời:

   

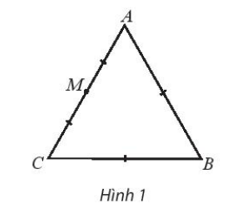
   Theo quy tắc ba điểm, ta có: $\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}$ = $\overrightarrow{\text{AC}}$
   Tam giác ABC đều cạnh bằng a nên AC = a.
   Do đó $\left|\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}\right|$ = $\left|\overrightarrow{AC}\right|$ = a.
   Gọi M là trung điểm cạnh AC.
   Ta có:
   $\overrightarrow{\text{AB}}-\overrightarrow{\text{BC}}\text{}$= $\overrightarrow{\text{AB}}+ \overrightarrow{CB}=\overrightarrow{\text{AB}} + \overrightarrow{CA}+\overrightarrow{\text{AB}}= 2\overrightarrow{\text{AB}} +2\overrightarrow{MA}=2(\overrightarrow{MA}+ \overrightarrow{\text{AB}} )=2\overrightarrow{MB}$ 
   Vì MB là đường trung tuyến của tam giác đều ABC cạnh bằng a nên MB = $\frac{\text{a}\sqrt{\text{3}}}{2}$.
   Do đó $\left|\overrightarrow{\text{AB}}-\overrightarrow{\text{BC}}\text{}\right|$ = 2$\left|\overrightarrow{MB}\right|$ = a$\sqrt{3}$.
   Vậy $\left|\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}\right|=a$ và $\left|\overrightarrow{\text{AB}}-\overrightarrow{\text{BC}}\text{}\right| = a\sqrt{3}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình bình hành ABCD tâm O. Chứng minh rằng: a) CO→−OB→=BA→​;
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD tâm O. Chứng minh rằng:
   a) $\overrightarrow{\text{CO}}-\overrightarrow{\text{OB}}=\overrightarrow{\text{BA}}\text{}$;

   Trả lời:

   

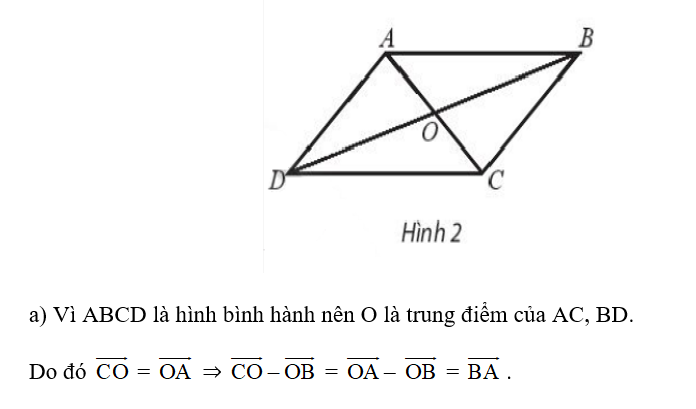
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====