Lý thuyết Toán lớp 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia
Video giải Toán 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia – Chân trời sáng tạo
A. Lý thuyết Hai đường thẳng cắt nhau, song song. Tia
1. Hai đường thẳng cắt nhau, song song
– Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.
Ví dụ 1. Hai đường thẳng a và b chỉ có một điểm chung là M, ta nói rằng hai đường thẳng a và b cắt nhau (như hình vẽ).
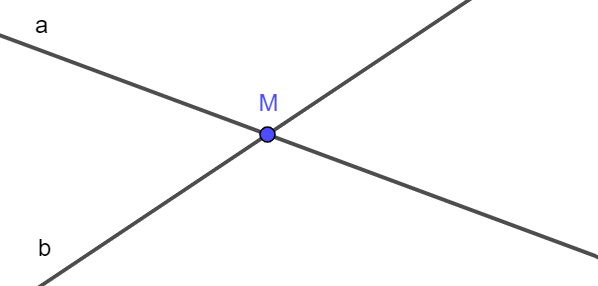
Khi đó, M là giao điểm của hai đường thẳng a và b.
– Nếu hai đường thẳng không có điểm chung nào, ta nói rằng hai đường thẳng đó song song với nhau.
Ví dụ 2. Hai đường thẳng c và d không có điểm chung nào (như hình vẽ).
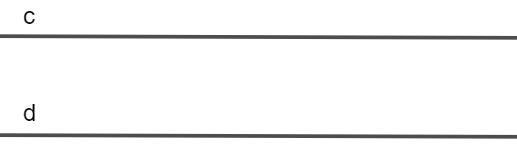
Khi đó, ta nói hai đường thẳng a và b song song với nhau.
Chú ý: Từ nay về sau, khi nói hai đường thẳng mà không nói gì thêm, ta hiểu đó là hai đường thẳng phân biệt.
2. Tia
Mỗi điểm O trên một đường thẳng chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc O.
Chú ý:
– Từ một điểm O kẻ một vạch thẳng về một phía của điểm O để biểu diễn một tia gốc O.
– Nếu A là một điểm tùy ý trên tia Ox, ta có thể gọi tia Ox là tia OA (như hình vẽ).

– Khi viết (đọc) tia, ta phải viết (đọc) gốc của tia trước.
Ví dụ 3. Cho hình vẽ.

Trong hình vẽ có O là điểm gốc.
Ta viết (đọc) gốc của tia trước, viết (đọc) là: tia Ox.
B. Bài tập tự luyện
Bài 1. Cho đường thẳng AB bất kỳ. Hãy vẽ hình trong các trường hợp sau:
a) Đường thẳng GH cắt đường thẳng AB;
b) Đường thẳng IK song song với đường thẳng AB.
Lời giải:
a) Đường thẳng GH cắt đường thẳng AB nên hai đường thẳng này có một điểm chung.
Chẳng hạn: vẽ hai đường thẳng GH và AB cắt nhau tại điểm M.
Cách vẽ:
Bước 1: Vẽ đường thẳng AB bất kỳ.

Bước 2: Lấy điểm M bất kỳ thuộc đường thẳng AB, giả sử điểm M nằm giữa hai điểm A và B.

Bước 3: Vẽ đường thẳng đi qua M và không trùng với đường thẳng AB.
Ta có đường thẳng GH cắt đường thẳng AB như hình vẽ:
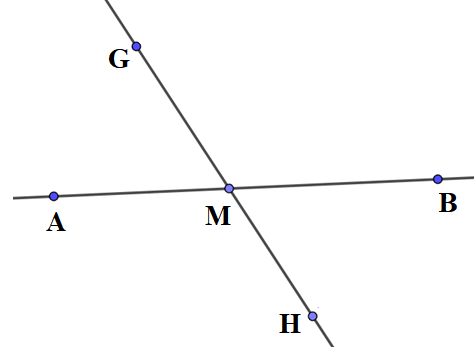
b) Cách vẽ đường thẳng IK song song với đường thẳng AB:
Bước 1: Vẽ đường thẳng AB bất kỳ.

Bước 2: Lấy điểm I nằm ngoài đường thẳng AB.
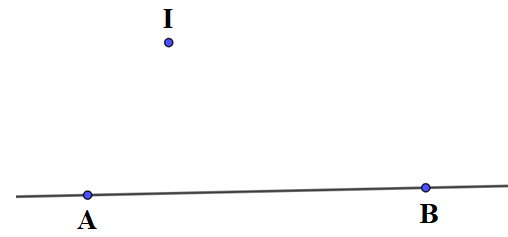
Bước 3: Vẽ đường thẳng đi qua điểm I và song song với đường thẳng AB. Lấy điểm K thuộc đường thẳng vừa vẽ.
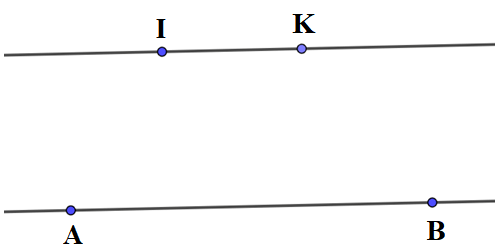
Ta được đường thẳng IK song song với đường thẳng AB như hình vẽ:
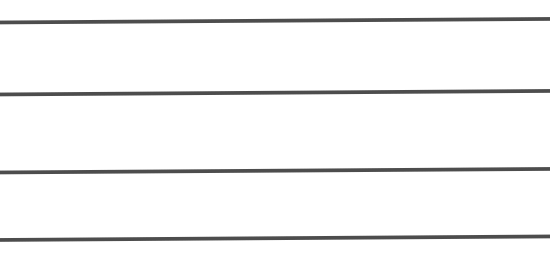
Bài 2. Đếm số giao điểm tạo bởi bốn đường thẳng trong mỗi hình sau:
a)
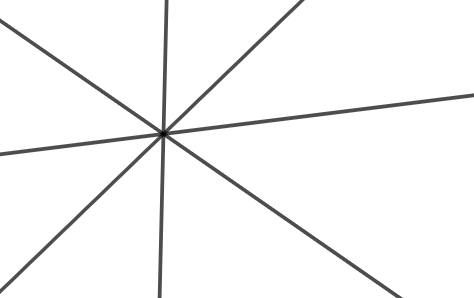
b)
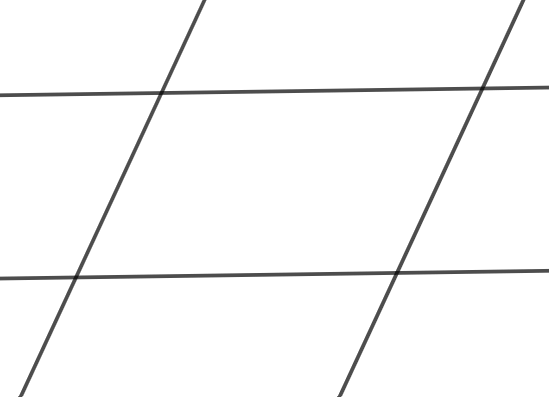
c)
Lời giải:
a) Trong hình a) có ba đường thẳng song song với nhau nên không có giao điểm nào.
b) Đặt các đường thẳng trong hình b) là các đường thẳng a, b, c, d.
Giả sử bốn đường thẳng a, b, c, d cắt nhau tại điểm M (như hình vẽ).
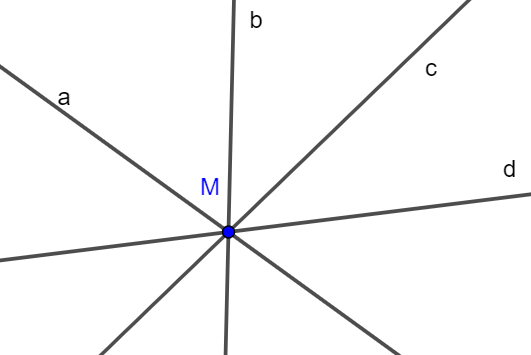
Vậy trong hình b) có một giao điểm tạo bởi bốn đường thẳng.
c) Đặt các đường thẳng trong hình c) là các đường thẳng m, n, p, q.
Giả sử đường thẳng m và p cắt nhau tại điểm A, đường thẳng n và p cắt nhau tại điểm B, đường thẳng m và q cắt nhau tại C, đường thẳng n và q cắt nhau tại D (như hình vẽ).
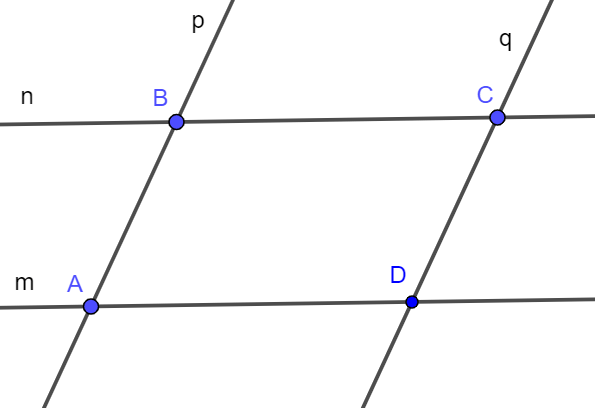
Do đó bốn đường thẳng m, n, p, q đôi một cắt nhau tại các điểm A, B, C, D.
Vậy trong hình c) có bốn giao điểm tạo bởi bốn đường thẳng.
Bài 3. Cho hai đường thẳng XY và EF cắt nhau tại điểm O. Kể tên các tia có gốc O.
Lời giải:
Cách vẽ:
– Vẽ đường thẳng XY bất kỳ.
– Lấy điểm O thuộc đường thẳng XY.
– Vẽ đường thẳng EF đi qua O (đường thẳng EF không trùng với đường thẳng XY).
Ta có hình vẽ:
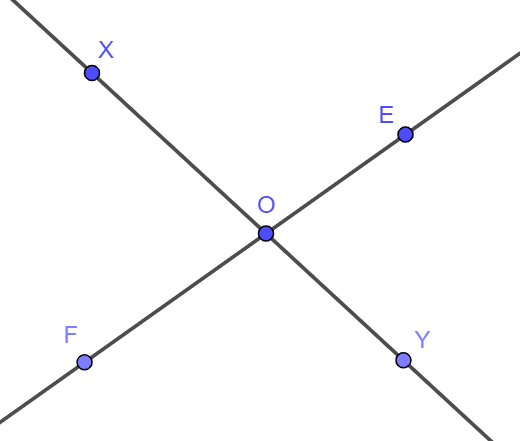
Hai đường thẳng XY và EF cắt nhau tại điểm O nên điểm O nằm trên hai đường thẳng này.
– Điểm O nằm trên đường thẳng XY nên điểm O chia đường thẳng XY thành hai tia có chung gốc O là tia OX, OY.
– Điểm O nằm trên đường thẳng EF nên điểm O chia đường thẳng EF thành hai tia có chung gốc O là tia OE, OF.
Vậy các tia có gốc O là: OX, OY, OE, OF.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Ba điểm thẳng hàng. Ba điểm không thẳng
Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
Bài 5: Trung điểm của đoạn thẳng
Bài 6: Góc
Bài 7: Số đo góc. Các góc đặc biệt
====== ****&**** =====