d) y=12x+1−6×2−5x−21

Câu hỏi:

d) $y=\frac{1}{\sqrt{2x+1}}-\sqrt{6x^2-5x-21}$

Trả lời:

d) Hàm số xác định khi và chỉ khi 2x + 1 > 0 và 6x² – 5x – 21 ≥ 0
+) Xét 2x + 1 > 0 khi và chỉ khi x >$\frac{-1}{2}$
+) Xét tam thức bậc hai f ( x ) = 6x² – 5x – 21 có ∆ = (–5)² – 4.6.( –21) = 529 > 0 suy ra f(x) hai nghiệm phân biệt x₁ =  $\frac{7}{3}$ và x₂ = $\frac{–3}{2}$  ,
Ta có a = 6 > 0 nên f ( x ) ≥ 0 khi và chỉ khi x ≤ $\frac{–3}{2}$  hoặc x ≥ $\frac{7}{3}$  mà x > $\frac{-1}{2}$  nên x ≥ $\frac{7}{3}$ .
Vậy tập xác định của hàm số là D = $\left[\frac{7}{3};+\infty \right)$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. x = 2 là một nghiệm của bất phương trình nào sau đây? a) x2−3x+1>0;
   
   

   Câu hỏi:
   

   x = 2 là một nghiệm của bất phương trình nào sau đây?
   a) $x^2-3x+1>0;$

   Trả lời:

   a) Thay x = 2 vào bất phương trình ta được: 2² – 3.2 +1 = –1 < 0.
   Vì vậy x = 2 không là nghiệm của bất phương trình $x^2-3x+1>0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. b) −4×2−3x+5≤0;
   
   

   Câu hỏi:
   

   b) $-4x^2-3x+5\le 0;$

   Trả lời:

   b) Thay x = 2 vào bất phương trình ta được: –4.2² – 3.2 +5 = –17 < 0.
   Vì vậy x = 2 là nghiệm của bất phương trình $-4x^2-3x+5\le 0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. c) 2×2−5x+2≤0
   
   

   Câu hỏi:
   

   c) $2x^2-5x+2\le 0$

   Trả lời:

   c) Thay x = 2 vào bất phương trình ta được: 2.2² – 5.2 + 2 = 0 ≤ 0
   Vì vậy x = 2 là nghiệm của bất phương trình $2x^2-5x+2\le 0$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng. a) fx≥0
   
   

   Câu hỏi:
   

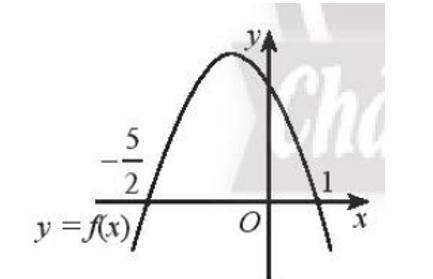
   Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng.
   a) $f\left(x\right)\ge 0$
   

   Trả lời:

   a) $\left[-\frac{5}{2};1\right]$
   Đồ thị hàm số bậc hai nằm phía trên trục hoành với $x\in \left(-\frac{5}{2};1\right)$ ;
   Đồ thị hàm số bậc hai cắt trục hoành tại hai điểm x = $-\frac{5}{2}$  và x = 1.
   Do đó f(x) ≥ 0 khi $\left[-\frac{5}{2};1\right]$ .
   Vậy tập nghiệm của bất phương trình f(x) ≥ 0 là S = $\left[-\frac{5}{2};1\right]$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) fx&lt;0
   
   

   Câu hỏi:
   

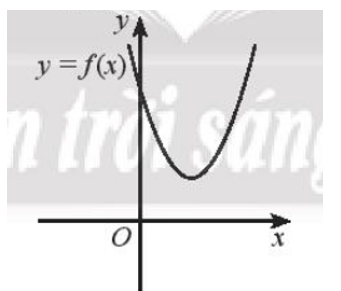
   b) $f\left(x\right)<0$
   

   Trả lời:

   b) Đồ thị hàm số bậc hai nằm phía trên trục hoành với mọi x ∈ ℝ hay f(x) > 0 với mọi x ∈ ℝ.
   Do đó f(x) < 0 vô nghiệm.
   Vậy tập nghiệm của bất phương trình f(x) < 0 là S = ∅.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====