Giải SBT Toán lớp 6 Bài 6: Lũy thừa với số mũ tự nhiên
Bài 1.51 trang 22 sách bài tập Toán lớp 6 Tập 1: Viết gọn các tích sau bằng cách dùng lũy thừa:
a) 2. 2. 2. 2. 2;
b) 2. 3. 6. 6. 6;
c) 4. 4. 5. 5. 5.
Lời giải:
a) 2. 2. 2. 2. 2 = 25
b) 2. 3. 6. 6. 6 = 6. 6. 6. 6 = 64
c) 4. 4. 5. 5. 5 = (4. 4). (5. 5. 5) = 42. 53
Bài 1.52 trang 22 sách bài tập Toán lớp 6 Tập 1:a) Lập bảng giá trị của 2n với n ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10};
b) Viết dưới dạng lũy thừa của 2 các số sau: 8; 256; 1 024; 2 048.
Lời giải:
a)
+) Với n = 0 thì 2n = 20 = 1 (theo quy ước)
+) Với n = 1 thì 2n = 21 = 2
+) Với n = 2 thì 2n = 22 = 2.2 = 4
+) Với n = 3 thì 2n = 23= 2.2.2 = 8
+) Với n = 4 thì 2n = 24 = 2.2.2.2 = 16
+) Với n = 5 thì 2n = 25 = 2.2.2.2.2 = 32
+) Với n = 6 thì 2n = 26 = 2.2.2.2.2.2 = 64
+) Với n = 7 thì 2n = 27 = 2.2.2.2.2.2.2 = 128
+) Với n = 8 thì 2n = 28 = 2.2.2.2.2.2.2.2 = 256
+) Với n = 9 thì 2n = 29 = 2.2.2.2.2.2.2.2.2 = 512
+) Với n = 10 thì 2n = 210 = 2.2.2.2.2.2.2.2.2.2 = 1024
Ta có bảng sau:
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
2n
|
1
|
2
|
4
|
8
|
16
|
32
|
64
|
128
|
256
|
512
|
1 024
|
b) Từ bảng trên ta thấy:
+) 8 = 23; 256 = 28 ; 1 024 = 210;
+) 2 048 = 2. 1 024 = 21.210 = 21+10 = 211
Bài 1.53 trang 23 sách bài tập Toán lớp 6 Tập 1:a) Viết các bình phương của hai mươi số tự nhiên đầu tiên thành một dãy theo thứ tự từ nhỏ đến lớn;
b) Viết các số sau thành bình phương của một số tự nhiên: 64; 100; 121; 169; 196; 289.
Lời giải:
a)
1) Với a = 0 thì a2 = 02 = 0.0 = 0
2) Với a = 1 thì a2 = 12 = 1.1 = 1
3) Với a = 2 thì a2 = 22 = 2.2 = 4
4) Với a = 3 thì a2 = 32 = 3.3 = 9
5) Với a = 4 thì a2 = 42 = 4.4 = 16
6) Với a = 5 thì a2 = 52 = 5.5= 25
7) Với a = 6 thì a2 = 62 = 6.6 = 36
8) Với a = 7 thì a2 = 72 = 7.7 = 49
9) Với a = 8 thì a2 = 82 = 8.8 = 64
10) Với a = 9 thì a2 = 92 = 9.9 = 81
11) Với a = 10 thì a2 = 102 = 10.10 = 100
12) Với a = 11 thì a2 = 112 = 11.11 = 121
13) Với a = 12 thì a2 = 122 = 12.12 = 144
14) Với a = 13 thì a2 = 132 = 13.13 = 169
15) Với a = 14 thì a2 = 142 = 14.14 = 196
16) Với a = 15 thì a2 = 152 = 15.15 = 225
17) Với a = 16 thì a2 = 162 = 16.16 = 256
18) Với a = 17 thì a2 = 172 = 17.17 = 289
19) Với a = 18 thì a2 = 182 = 18.18 = 324
20) Với a = 19 thì a2 = 192 = 19.19 = 361
Vậy các bình phương của hai mươi số tự nhiên đầu tiên thành một dãy theo thứ tự từ nhỏ đến lớn là: 0; 1; 4; 9; 16; 25; 36; 49; 64; 81; 100; 121; 144; 169; 196; 225; 256; 289; 324; 361.
b)
+) 64 = 8. 8 = 82
+) 100 = 10. 10 = 102
+) 121 = 11. 11 = 112
+) 196 = 14. 14 = 142
+) 289 = 17. 17 = 172
Bài 1.54 trang 23 sách bài tập Toán lớp 6 Tập 1:a) Tính nhẩm 10n với n ∈ {0; 1; 2; 3; 4; 5}. Phát biểu quy tắc tổng quát tính lũy thừa của 10 với số mũ đã cho;
b) Viết dưới dạng lũy thừa của 10 các số sau: 10; 10 000; 100 000; 10 000 000; 1 tỉ.
Lời giải:
a) Ta có:

b) 10 = 101; 10 000 = 104; 100 000 = 105; 10 000 000 = 107; 1 tỉ = 1 000 000 000 = 109.
Bài 1.55 trang 23 sách bài tập Toán lớp 6 Tập 1: Tính:
a) 25
b) 52
c) 24. 32.7
Lời giải:
a) 25= 2.2.2.2.2 = 4.2.2.2 = 8.2.2 = 16.2 = 32
b) 52 = 5. 5 = 25
c) 24. 32.7 = (2. 2. 2. 2). (3.3).7 = (4. 2. 2). 9. 7 = 8. 2. 9. 7 = 16. 9. 7 = 144. 7 = 1 008.
Bài 1.56 trang 23 sách bài tập Toán lớp 6 Tập 1: Tìm n, biết:
a) 54= n
b) n3 = 125
c) 11n = 1331;
Lời giải:
a) 54 = n;
Hay n = 54 = 5. 5. 5. 5 = 25. 5. 5 = 125. 5 = 625
Vậy n = 625.
b) n3 = 125;
n3 = 5.5.5
n3 = 53
n = 5
Vậy n = 5.
c) 11n = 1331
11n = 11.11.11
11n = 113
Vậy n = 3.
Bài 1.57 trang 23 sách bài tập Toán lớp 6 Tập 1: Viết kết quả các phép tính sau dưới dạng một lũy thừa:
a) 3.34.35
b) 73:72:7
c) (x4)3.
Lời giải:
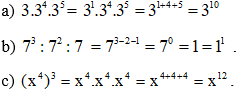
Bài 1.58 trang 23 sách bài tập Toán lớp 6 Tập 1: Kết luận sau đúng hay sai?
Không có số chính phương nào có chữ số hàng đơn vị là 2.
Lời giải:
Các số tự nhiên có chữ số tận cùng là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 khi bình phương sẽ có chữ số tận cùng lần lượt là 0; 1; 4; 9; 6; 5; 6; 9; 4; 1. Do đó số chính phương bất kì sẽ có chữ số tận cùng là 0; 1; 4; 5; 6; 9.
Vì vậy kết luận không có số chính phương nào có chữ số hàng đơn vị là 2 là đúng.
Bài 1.59 trang 23 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số tận cùng của số 475 và chứng tỏ số 475 + 20216 không phải là số chính phương.
Lời giải:
+) Ta thấy: 472 = 47 . 47 = 47 . (40 + 7) = 47 . 40 + 47. 7 = 47. 40 + (40 + 7) . 7
= 47 . 40 + 40 . 7 + 7 . 7 = 47 . 40 + 40 . 7 + 49
Vì 47 . 40 có chữ số tận cùng là 0; 40 . 7 có chữ số tận cùng là 0; 49 có chữ số tận cùng là 9 nên 472 có chữ số tận cùng của là 0 + 0 + 9 = 9.
Tương tự (472)2 có chữ số tận cùng như chữ số tận cùng của 92 = 81 nên chữ số tận cùng của (472)2 là 1.
Do đó: 475 = 472 + 2 + 1 = 472 . 472 . 47 = (472)2 . 47 có chữ số tận cùng của là 1 . 7 = 7.
Vì vậy chữ số tận cùng của số 475 là 7.
+) Ta có 2 021 có chữ số tận cùng là 1 nên
2 0216 = 2 021 . 2 021 . 2 021 . 2 021 . 2 021 . 2 021 có chữ số tận cùng của 1 . 1 . 1 . 1 . 1 . 1 là 1.
Vì vậy chữ số tận cùng của số 2 0216 là 1.
Như vậy 475 + 2 0216 có chữ số tận cùng là 7 + 1 = 8.
Mà các số tự nhiên thì có chữ số tận cùng là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 khi bình phương sẽ có chữ số tận cùng lần lượt là 0; 1; 4; 9; 6; 5; 6; 9; 4; 1. Do đó số chính phương bất kì sẽ có chữ số tận cùng là 0; 1; 4; 5; 6; 9.
Vậy 475 + 2 0216 có chữ số tận cùng là 8 thì không phải là số chính phương.
Bài 1.60 trang 23 sách bài tập Toán lớp 6 Tập 1: Không tính các lũy thừa, hãy so sánh:
a) 2711 và 818
b) 6255 và 1257
c) 536 và 1124
Lời giải:
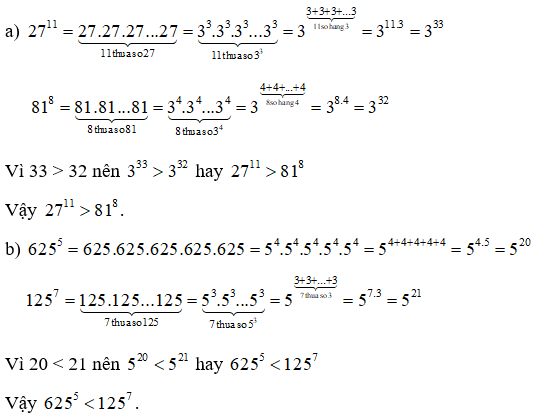
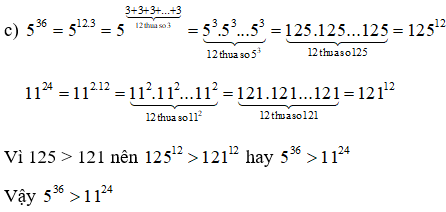
Bài 1.61 trang 23 sách bài tập Toán lớp 6 Tập 1: Giải thích tại sao ba số sau đều là số chính phương:
a) A = 11 – 2
b) B = 1 111 – 22
c) C = 111 111 – 222
Lời giải:
a) A = 11 – 2 = 9 = 3. 3 = 32
Do đó A là số chính phương.
b) B = 1 111 – 22
= (1 100 + 11) – (11 + 11)
= 1 100 – 11
= 11. 100 – 11. 1
= 11. (100 – 1)
= 11. 99
= 11. (9. 11)
= (11. 11). 9
= (11. 11). (3. 3)
= (11.3). (11. 3)
= 33. 33
= 332
Do đó B là số chính phương.
c) C = 111 111 – 222
= (111 000 + 111) – (111 + 111)
= 111 000 – 111
= 111. 1 000 – 111. 1
= 111. (1 000 – 1)
= 111. 999
= 111. (111. 9)
= (111. 111). 9
= (111. 111). (3. 3)
= (111. 3). (111. 3)
= 333. 333
= 3332
Do đó C là số chính phương.
Vậy cả ba số A, B, C đều là số chính phương.
====== ****&**** =====