Một hình thang có chiều cao là 10 m, hiệu 2 đáy là 22 m. Kéo dài đáy nhỏ bằng đáy lớn để hình đã cho thành hình chữ nhật có chiều daid bằng đáy lớn, chiều rộng bằng chiều cao hình thang. Diện tích được mở rộng thêm bằng 1/7 diện tích hình thang cũ. Phần mở rộng về phía tay phải có diện tích là 90 m2. Tính đáy lớn của hình thang ban đầu.

Câu hỏi:

Một hình thang có chiều cao là 10 m, hiệu 2 đáy là 22 m. Kéo dài đáy nhỏ bằng đáy lớn để hình đã cho thành hình chữ nhật có chiều daid bằng đáy lớn, chiều rộng bằng chiều cao hình thang. Diện tích được mở rộng thêm bằng 1/7 diện tích hình thang cũ. Phần mở rộng về phía tay phải có diện tích là 90 m². Tính đáy lớn của hình thang ban đầu.

Trả lời:

Đáy BG của ∆ CBG là : 90 x 2 : 10 = 18 (m)      Đáy EA của ∆ DAE là : 22 – 18 = 4 (m)Diện tích 2 phần mở rộng là : 20 + 90 = 110 (m²Diện tích hình thang ABCD là 110 x 7 = 770 (m²)      Tổng hai đáy AB và CD là : 770 x 2 : 10 = 154 (m)   Đáy CD là : (154 + 22) : 2 = 88 (m)                                                                                                

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giải Toán 8 Bài 2: Hình thang
   Giải bài tập Toán lớp 8 Bài 2: Hình thang

   Trả lời câu hỏi giữa bài

   Trả lời câu hỏi 1 trang 69 sgk Toán 8 Tập 1:

   

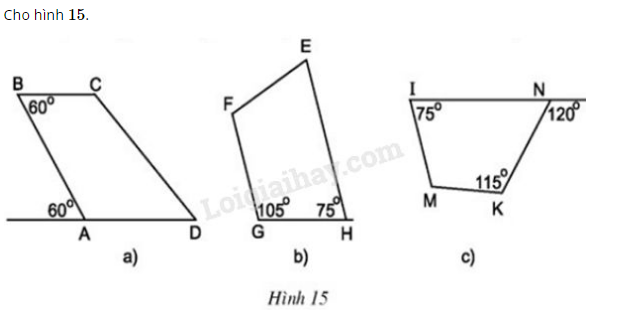
   a) Tìm các tứ giác là hình thang.

   Phương pháp giải: Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.

   Lời giải:

   Tứ giác $ABCD$ là hình thang vì $BC//AD$ (có hai góc so le trong bằng nhau) 

   Tứ giác $EFGH$ là hình thang vì $FG//EH$ (có tổng hai góc trong cùng phía bằng ${105}^o+{75}^o={180}^o$)

   Tứ giác $IMKN$ không phải là hình thang vì không có cặp cạnh đối nào song song (do IM không song song NK; góc N và góc K ở vị trí nhưng không bằng nhau nên MK không song song IN).

   b) Có nhận xét gì về hai góc kề một cạnh bên của hình thang ?

   Phương pháp giải: Quan sát và rút ra nhận xét

   Lời giải:

   Hai góc kề một cạnh bên của hình thang bù nhau.

   Trả lời câu hỏi 2 trang 70 sgk Toán 8 Tập 1:

   

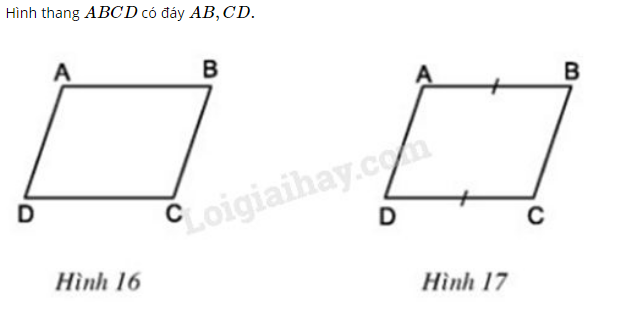
   a) Cho biết $AD//BC$ (h.16). Chứng minh rằng $AD=BC,AB=CD.$

   b) Cho biết $AB=CD$ (h.17). Chứng minh rằng $AD//BC,AD=BC.$

   Phương pháp giải: Áp dụng:

   – Xét hai tam giác bằng nhau

   – Hai đường thẳng song song thì có cặp góc so le trong bằng nhau.

   Lời giải:

   a)

   

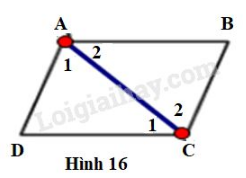
   Hình thang $ABCD$ có đáy $AB,CD\Rightarrow AB//CD\Rightarrow \widehat{A_2}=\widehat{C_1}$ (hai góc so le trong) 

   Lại có: $AD//BC$ $\Rightarrow \widehat{A_1}=\widehat{C_2}$ (hai góc so le trong)

   Xét $\Delta ABC$ và $\Delta CDA$ có:

   +) $\widehat{A_2}=\widehat{C_1}$ (chứng minh trên)

   +) $AC$ chung

   +) $\widehat{A_1}=\widehat{C_2}$ (chứng minh trên)

   $\Rightarrow \Delta ABC=\Delta CDA$ (g.c.g)

   $\Rightarrow AD=BC,AB=CD$ (các cặp cạnh tương ứng)

   b)

   

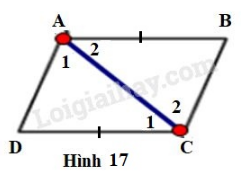
   Hình thang $ABCD$ có đáy $AB,CD\Rightarrow AB//CD\Rightarrow \widehat{A_2}=\widehat{C_1}$ (hai góc so le trong) 

   Xét $\Delta ABC$ và $\Delta CDA$ có:

   +) $AC$ chung

   +) $\widehat{A_2}=\widehat{C_1}$  (chứng minh trên)

   +) $AB=CD$ (giả thiết)

   $\Rightarrow \Delta ABC=\Delta CDA$ (c.g.c)

   $\Rightarrow AD=BC$ (hai cạnh tương ứng)

   $\Rightarrow$ $\widehat{A_1}=\widehat{C_2}$ (hai góc tương ứng)

   Mặt khác $\widehat{A_1};\widehat{C_2}$ ở vị trí so le trong.

   $\Rightarrow AD//BC$

   Câu hỏi và bài tập (trang 70, 71 sgk Toán 8 Tập 1)

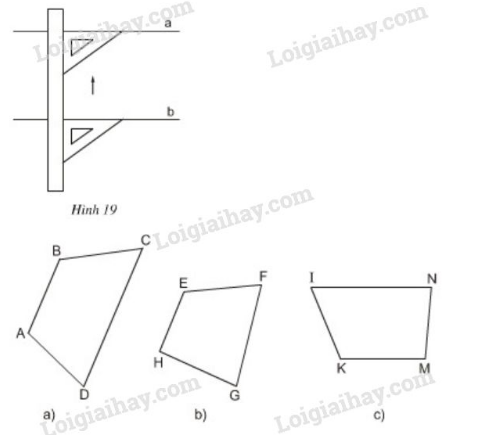
   Bài 6 trang 70 sgk Toán 8 Tập 1: Dùng thước và êke, ta có thể kiểm tra được hai đường thẳng có song song với nhau hay không (xem hình ). Trên hình , có những tứ giác nào là hình thang, có những tứ giác nào không là hình thang. Bằng cách nêu trên, hãy kiểm tra xem trong các tứ giác ở hình , tứ giác nào là hình thang?

   

   Phương pháp giải: Áp dụng:

   – Định nghĩa hai đường thẳng song song: là hai đường thẳng không có điểm chung.

   – Định nghĩa hình thang: Hình thang là tứ giác có hai cạnh đối song song.

   Lời giải:

   Các bước tiến hành:

   – Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.

   – Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.

   – Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.

   – Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.

   Bằng cách kiểm tra trên ta có kết quả như sau:

   +) Tứ giác $ABCD$ có cạnh $AB$ song song với cạnh $DC$ nên tứ giác $ABCD$ là hình thang.

   +) Tứ giác $IKMN$ có cạnh $IN$ song song với cạnh $KM$ nên tứ giác $IKMN$ là hình thang.

   +) Tứ giác $EFGH$ không là hình thang vì không có cặp cạnh nào song song với nhau.

   Bài 7 trang 71 sgk Toán 8 Tập 1:

   

   Phương pháp giải: Áp dụng các tính chất của một đường thẳng cắt hai đường thẳng song song: hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau.

   Lời giải:

   Vì $ABCD$ là hình thang có đáy là $AB$ và $CD$ nên $AB//CD$

   $a)$ Ta có: $AB//DC$ (chứng minh trên) 

   $\Rightarrow \hat{A}+\hat{D}={180}^0$ (hai góc trong cùng phía bù nhau)

   $\Rightarrow x+{80}^0={180}^0$ 

   $\Rightarrow x={180}^0-{80}^0={100}^0$

   Ta có: $AB//DC$ (chứng minh trên)

   $\Rightarrow \hat{C}+\hat{B}={180}^0$ (hai góc trong cùng phía bù nhau)

   $\Rightarrow y+{40}^0={180}^0$

   $\Rightarrow y={180}^0-{40}^0={140}^0$

   $b)$ Vì $AB//DC$ (chứng minh trên)

   $\Rightarrow x={70}^0$ (hai góc đồng vị bằng nhau)

   $\Rightarrow y={50}^0$ (hai góc so le trong bằng nhau)

   $c)$ Ta có $AB//DC$ (chứng minh trên)

   $\Rightarrow \hat{B}+\hat{C}={180}^0$ (hai góc trong cùng phía bù nhau)

   $\Rightarrow x+{90}^0={180}^0$

   $\Rightarrow x={180}^0-{90}^0={90}^0$

   Ta có $AB//DC$ (chứng minh trên)

   $\Rightarrow \hat{D}+\hat{A}={180}^0$ (hai góc trong cùng phía bù nhau)

   $\Rightarrow y+{65}^0={180}^0$

   $\Rightarrow y={180}^0-{65}^0={115}^0$

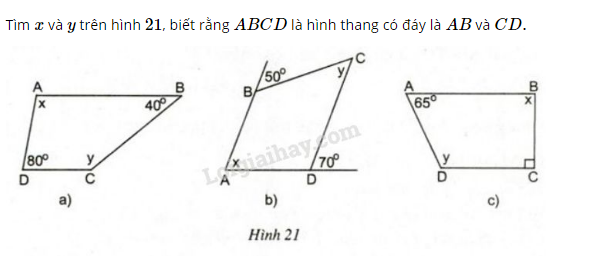
   Bài 8 trang 71 sgk Toán 8 Tập 1: Hình thang $ABCD$ ($AB//CD$) có $\hat{A}-\hat{D}={20}^0$   , $\hat{B}=2\hat{C}$. Tính các góc của hình thang.

   Phương pháp giải: Áp dụng tính chất: Nếu một đường thẳng cắt hai đường thẳng song song thì tổng hai góc trong cùng phía bù nhau.
   Lời giải: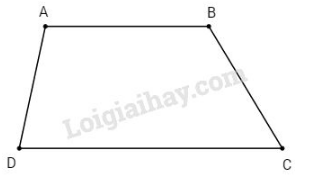

   

   Vì $AB//CD$ nên $\hat{A}+\hat{D}={180}^0$  (1) (hai góc trong cùng phía bù nhau)

   Ta có $\hat{A}-\hat{D}={20}^0$ (giả thiết) 

   $\begin{array}{l}\Rightarrow \hat{A}=\hat{D}+{20}^0(2)\\ \text{Thay (2) vào (1) ta được:}\\ \Rightarrow \hat{A}+\hat{D}=\hat{D}+{20}^0+\hat{D}\\ =2\hat{D}+{20}^0={180}^0\\ \Rightarrow \hat{D}=\left({180}^0-{20}^0\right):2={80}^0.\end{array}$

   Thay $\hat{D}={80}^0$ vào $\hat{A}={20}^0$ +$\hat{D}$ ta được $\hat{A}={20}^0+{80}^0={100}^0$

   Lại có $\hat{B}=2\hat{C}$     (3) ;

   Do $AB//CD$ nên $\hat{B}+\hat{C}={180}^0$   (4) (hai góc trong cùng phía bù nhau)

   Thay (3) vào (4) ta được:

   $2\hat{C}+\hat{C}={180}^0$

   hay $3\hat{C}={180}^0\Rightarrow \hat{C}={180}^0:3={60}^0$

   Do đó $\hat{B}=2\hat{C}={2.60}^0={120}^0$

   Bài 9 trang 71 sgk Toán 8 Tập 1: Tứ giác $ABCD$ có $AB=BC$ và $AC$ tia phân giác của góc $A$. Chứng minh rằng $ABCD$ là hình thang.

   Phương pháp giải: Áp dụng:

   – Dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.

   – Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.

   Lời giải:

   

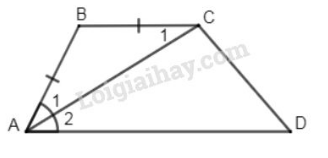
   Ta có $AB=BC$ (giả thiết)

   Suy ra  $∆ABC$ cân tại $B$ (định nghĩa tam giác cân)

   Nên $\widehat{A_1}=\widehat{C_1}$ (1) (tính chất tam giác cân) 

   Lại có, $AC$ là tia phân giác của $\hat{A}$ (giả thiết) nên suy ra $\widehat{A_1}=\widehat{A_2}$ (2) (tính chất tia phân giác )

   Từ (1) và (2) suy ra $\widehat{C_1}=\widehat{A_2}$ mà hai góc này ở vị trí so le trong nên $BC//AD$

   Vậy tứ giác $ABCD$ là hình thang.

   Bài 10 trang 71 sgk Toán 8 Tập 1:

   

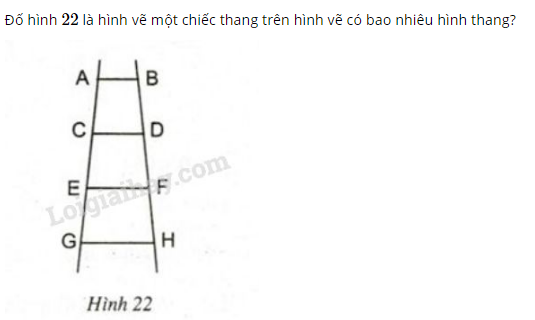
   Phương pháp giải: Áp dụng dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.

   Lời giải:

   Từ hình 22 ta có: $AB//CD//EF//GH$

   Nên ta có tất cả $6$ hình thang, đó là: $ABDC,CDFE,EFHG,$ $ABFE,CDHG,ABHG.$

   Lý thuyết hình thang

   1. Các kiến thức cần nhớ:

   * Hình thang: 

   Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.

   Hai góc kề một cạnh bên của hình thang có tổng bằng ${180}^0$

   Nhận xét: 

   + Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.

   + Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.

   + Hình thang vuông là hình thang có một góc vuông.

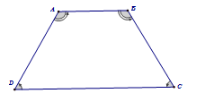
   Ví dụ 1:

   

   $ABCD$ là hình thang. Khi đó:

   + $AB//CD$ , $AB,CD$ là hai đáy, $AD,BC$ là cạnh bên.

   + $\hat{A}+\hat{D}=\hat{B}+\hat{C}={180}^{\circ }$

   + Nếu $AD//BC\iff \{\begin{array}{l}AD=BC\\ AB=CD\end{array}$

   + Nếu $AB=CD\iff \{\begin{array}{l}AD=BC\\ AD//BC\end{array}$

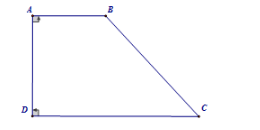
   * Hình thang vuông:  là hình thang có  thì  là hình thang vuông.

   

   * Hình thang cân: 

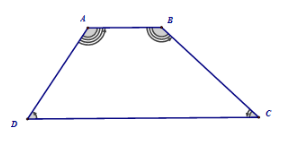
   Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
   

   Tính chất:

   + Trong hình thang cân, hai cạnh bên bằng nhau.

   + Trong hình thang cân, hai đường chéo bằng nhau.

   Dấu hiệu nhận biết:

   + Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

   + Hình thang có hai đường chéo bằng nhau là hình thang cân.

   Ví dụ:

   + $ABCD$ là hình thang cân thì $AD=BC;AC=BD$

   + Tứ giác $ABCD$ có $\{\begin{array}{l}AB//CD\\ \hat{D}=\hat{C}\end{array}$ $\iff ABCD$ là hình thang cân.

   + Tứ giác $ABCD$ có $\{\begin{array}{l}AB//CD\\ \hat{A}=\hat{B}\end{array}$ $\iff ABCD$ là hình thang cân.

   + Tứ giác $ABCD$ có $\{\begin{array}{l}AB//CD\\ AC=BD\end{array}$ $\iff ABCD$ là hình thang cân.

   2. Các dạng toán thường gặp:

   Dạng 1: Chứng minh và tính các góc của hình thang, hình thang vuông hình thang cân dựa vào tính chất hình.

   Phương pháp: Ta sử dụng các kiến thức:

   + Tính chất của hình thang, hình thang vuông, hình thang cân (ở trên)

   + Tổng bốn góc của một tứ giác bằng${360}^{\circ }$ .

   + Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.

   + Hai góc kề một cạnh bên của hình thang bằng ${180}^0$ .

   Dạng 2: Chứng minh một tứ giác là hình thang, hình thang vuông, hình thang cân

   Phương pháp: Ta sử dụng định nghĩa và các dấu hiệu nhận biết để chứng minh

   

    
2. 12 câu Trắc nghiệm Hình thang. Diện tích hình thang có đáp án 2023 -Toán lớp 5
   Giới thiệu về tài liệu:

   – Số trang: 8 trang

   – Số câu hỏi trắc nghiệm: 12 câu

   – Lời giải & đáp án: có

   Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Hình thang. Diện tích hình thang có đáp án – Toán lớp 5:

   

   Hình thang. Diện tích hình thang

   Câu 1: Điền số thích hợp vào ô trống:

   Cho hình thang như hình vẽ:

   

   Diện tích hình thang đã cho là  cm².

   Diện tích hình thang đó là:

    = 711 (cm²)

   Đáp số: 711cm².

   Vậy đáp án đúng điền vào ô trống là 711.

   Câu 2: Điền số thích hợp vào ô trống:

   Trung bình cộng hai đáy hình thang là 17,5m. Biết đáy lớn hơn đáy bé 13m. Chiều cao bằng  đáy lớn.

   Vậy diện tích hình thang đó là  m².

   Tổng độ dài hai đáy của hình thang là:

   17,5 × 2 = 35 (m)

   Độ dài đáy lớn của hình thang là:

   (35+ 13) : 2 = 24 (m)

   Độ dài đáy bé của hình thang là:

   35 −24 = 11 (m)

   Chiều cao của hình thang là:

   24 × 34 = 18 (m)

   Diện tích của hình thang là:

   (24 + 11) × 18 : 2 = 315 (m²)

   Đáp số: 315m².

   Vậy đáp án đúng điền vào ô trống là 315.

   Câu 3: Điền số thích hợp vào ô trống:

   Cho hình chữ nhật ABCD có AB = 24,4cm; BC = 11cm. Điểm M nằm trên cạnh AB sao cho AM =  AB.

   

   Diện tích hình thang AMCD là  cm².

   Vì ABCD là hình chữ nhật nên AB = CD = 24,4cm; AD= BC = 11cm.

   Hình thang AMCD có chiều cao là AD = 11cm.

   Độ dài cạnh AM là:

   24,4 ×  = 14,64 (cm)

   Diện tích hình thang AMCD là:

    = 214,72 (cm²)

   Đáp số: 214,72cm².

   Câu 4: Điền số thích hợp vào ô trống:

   Cho hình thang ABCD có diện tích là 9,18m²; đáy bé AB = 1,7m; đáy lớn CD gấp hai lần đáy bé AB.

   Vậy chiều cao AH là  m.

   Độ dài đáy lớn CD là:

   1,7 × 2 = 3,4 (cm)

   Chiều cao AH dài là:

   9,18 × 2 : (1,7 + 3,4) = 3,6 (m)

   Đáp số: 3,6m.

   Vậy đáp án đúng điền vào ô trống là 3,6.

   Câu 5: Điền số thích hợp vào ô trống:

   Một mảnh vườn hình thang có chiều cao 22m; đáy bé bằng 17,5m và kém đáy lớn 9m. Người ta dự định dùng  diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam.

   Vậy diện tích đất trồng cam là  m².

   Độ dài đáy lớn của mảnh vườn là:

   17,5 + 9 = 26,5 (m)

   Diện tích mảnh vườn đó là:

   (17,5 + 26,5) × 22 : 2 = 484 (m²)

   Diện tích đất để trồng xoài là:

   484 × 14 = 121 (m²)

   Diện tích đất để trồng cam là:

   484 − 121 = 363 (m²)

   Đáp số: 363m².

   Vậy đáp án đúng điền vào ô trống là 363.

   Câu 6: Một hình thang có đáy lớn là a, đáy bé là b, chiều cao là h. Khi đó công thức tính diện tích hình thang đó là:

   

   Muốn tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

   Do đó, hình thang có đáy lớn là a, đáy bé là b, chiều cao là h thì diện tích hình thang đó được tính theo công thức:

   

   Câu 7: Tính diện tích hình thang biết độ dài đáy là 17cm và 12cm, chiều cao là 8cm.

   A. 40cm²

   B. 58cm²

   C. 116cm²

   D. 232cm²

   Diện tích hình thang đó là:

    = 116 (cm² )

   Đáp số: 116cm².

   Câu 8: Hình thang ABCD có chiều cao AH bằng 75cm; đáy bé bằng  đáy lớn. Biết diện tích hình thang bằng diện tích hình chữ nhật có chiều dài 135cm; chiều rộng 50cm. Tính độ dài đáy lớn, đáy bé của hình thang.

   A. Đáy lớn 54cm; đáy bé 36cm

   B. Đáy lớn 90cm; đáy bé 60cm

   C. Đáy lớn 72cm; đáy bé 48cm

   D. Đáy lớn 108cm; đáy bé 72cm

   Diện tích hình chữ nhật là:

   135 × 50 = 6750 (cm²)

   Vậy hình thang có diện tích là 6750cm².

   Tổng độ dài hai đáy của hình thang là:

   6750 × 2 : 75 = 180 (cm)

   Ta có sơ đồ:

   

   Theo sơ đồ, tổng số phần bằng nhau là:

   2 + 3 = 5 (phần)

   Giá trị một phần là:

   180 : 5 =36 (cm)

   Độ dài đáy lớn là:

   36 × 3 = 108 (cm)

   Độ dài đáy bé là:

   180 – 108 = 72 (cm)

   Đáp số: Đáy lớn 108cm; đáy bé 72cm.

   Câu 9: Điền số thích hợp vào ô trống:

   Diện tích hình thang có đáy lớn là 45dm, đáy bé là 25dm và chiều cao là 2m là  dm²

   Đổi 2m = 20dm

   Diện tích hình thang đó là:

    = 700 (dm²)

   Đáp số: 700dm²

   Vậy đáp án đúng điền vào ô trống là 700.

   Câu 10: Một thửa ruộng hình thang có đáy bé bằng  đáy lớn, chiều cao bằng  đáy lớn. Biết đáy lớn hình thang là 260m. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần 0,75 giờ cho mỗi 100m² đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?

   A. 76,05 giờ

   B. 101,4 giờ

   C. 180 giờ

   D. 202,8 giờ

   Độ dài đáy bé của thửa ruộng đó là:

   260 × 35 = 156 (m)

   Chiều cao của thửa ruộng đó là:

   260 × 14 = 65 (m)

   Diện tích của thửa ruộng đó là:

   (156 + 260) × 652 = 13520 (m²)

   13520m² gấp 100m² số lần là:

   13520: 100 = 135,2 (lần)

   Bác Hùng cần dùng số giờ để làm sạch cỏ trên cả thửa ruộng đó là:

   0,75 × 135,2 = 101,4 (giờ)

   Đáp số: 101,4 giờ.

   Câu 11: Điền số thích hợp vào ô trống:

   Cho hình thang có độ dài hai đáy lần lượt là 15,6m và 9,5m. Nếu kéo dài đáy lớn thêm 1,75m thì diện tích tăng thêm 7m².

   Vậy diện tích hình thang ban đầu là  dm².

   Theo bài ra ta có hình vẽ:

   

   Phần diện tích tăng thêm chính là diện tích của hình tam giác có đáy là 1,75m và chiều cao cũng chính là chiều cao của hình thang.

   Chiều cao của hình thang là:

   7 × 2 : 1,75 = 8 (m)

   Diện tích hình thang là:

   (15,6 + 9,5) × 8 : 2 = 100,4 (m²)

   100,4m² = 10040dm²

   Đáp số: 10040dm².

   Vậy đáp án đúng điền vào ô trống là 10040.

   Câu 12: Trong các hình sau, hình nào là hình thang?

   

   Quan sát các hình đã cho ta thấy các hình thứ nhất, thứ ba và thứ tư có một cặp cạnh đối diện song song nên các hình đó là hình thang.

   Xem thêm
3. 50 Bài tập Hình thang (có đáp án)- Toán 5
   Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 3 Bài 90: Hình thang. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 90: Hình thang. Mời các bạn đón xem:

   Bài tập Toán 5 Bài 90: Hình thang

   A. Bài tập Hình thang

   I. Bài tập trắc nghiệm

   Câu 1: Chọn đáp án đúng nhất.

   A. Hình vuông là một hình thang.

   B. Hình chữ nhật cũng là một hình thang vuông.

   C. Một hình vuông bao giờ cũng là một hình thang vuông

   D. Cả ba đáp án trên đều đúng.

   Câu 2: Trong các hình thang ở hình bên, hình nào là hình thang vuông:

   

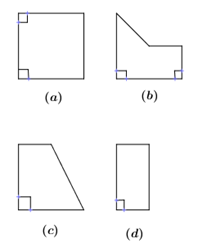
   A. Hình (a) và hình (c)             

   B. Hình (c) và (b)           

   C. Hình (a), hình (c) và hình (d)

   D. Cả bốn hình.

   Câu 3: Một hình thang có đáy lớn 5m, đáy bé 3m và chiều cao 2m. Diện tích của hình thang đó là:

   A. $8,5{\mathrm{m}}^2$

   B. $8{\mathrm{m}}^2$

   C. $9{\mathrm{m}}^2$

   D. $7,5{\mathrm{m}}^2$

   Câu 4: Một hình thang có đáy lớn 22dm. Đáy lớn gấp đôi đáy bé. Chiều cao bằng $\frac{3}{2}$ đáy bé. Diện tích hình thang đó là:

   A. $540,5{\mathrm{dm}}^2$

   B. $503,5{\mathrm{dm}}^2$

   C. $530,5{\mathrm{dm}}^2$

   D. $\mathrm{272,25\hspace{0.17em}}{\mathrm{dm}}^2$

   Câu 5: Một hình thang có độ dài đáy lớn bằng 130% chiều rộng, biết chiều rộng bằng 70cm. Chiều cao hình thang là 30cm. Diện tích hình thang đó là:

   A. $2417{\mathrm{cm}}^2$

   B. $2418{\mathrm{cm}}^2$

   C. $2415{\mathrm{cm}}^2$

   D. $2416{\mathrm{cm}}^2$

   Câu 6: Tính chiều cao của hình thang, biết rằng diện tích hình thang đó  bằng diện tích hình vuông có độ dài cạnh là 15cm. Tổng độ dài đáy lớn và đáy bé là $37,5\mathrm{cm}$ .

   A. 12cm

   B. 13cm

   C. 14cm

   D. 15cm

   Câu 7: Một hình thang có diện tích $360{\mathrm{m}}^2$, biết tổng hai đáy là 48m. Chiều cao của hình thang đó là:

   A.18m

   B. 15m

   C. 16,5m

   D. 17m

   Câu 8: Diện tích một cái ao hình thang là $166{\mathrm{m}}^2$, đáy lớn hơn đáy bé 4,2m. Chiều cao 10m. Độ dài đáy lớn đáy bé theo thứ tự là:  

   A. 18,7m và 14,5m

   B. 17,5m và 13,3m

   C. 19,2m và 15m

   D. 19,8m và 15,6m

   II. Bài tập tự luận

   Câu 1: Điền số thích hợp vào ô trống:

   Cho hình chữ nhật ABCD có AB = 24,4cm; BC = 11cm. Điểm M nằm trên cạnh AB sao cho AM =  AB.

   

   Diện tích hình thang AMCD là  cm².

   Đáp án
   

   Vì ABCD là hình chữ nhật nên AB = CD = 24,4cm; AD= BC = 11cm.

   Hình thang AMCD có chiều cao là AD = 11cm.

   Độ dài cạnh AM là:

   24,4 ×  = 14,64 (cm)

   Diện tích hình thang AMCD là:

    = 214,72 (cm²)

   Đáp số: 214,72cm².

   Câu 2: Điền số thích hợp vào ô trống:

   Cho hình thang ABCD có diện tích là 9,18m²; đáy bé AB = 1,7m; đáy lớn CD gấp hai lần đáy bé AB.

   Vậy chiều cao AH là  m.

   Đáp án
   

   Độ dài đáy lớn CD là:

   1,7 × 2 = 3,4 (cm)

   Chiều cao AH dài là:

   9,18 × 2 : (1,7 + 3,4) = 3,6 (m)

   Đáp số: 3,6m.

   Vậy đáp án đúng điền vào ô trống là 3,6.

   Câu 3: Điền số thích hợp vào ô trống:

   Một mảnh vườn hình thang có chiều cao 22m; đáy bé bằng 17,5m và kém đáy lớn 9m. Người ta dự định dùng  diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam.

   Vậy diện tích đất trồng cam là  m².

   Đáp án
   

   Độ dài đáy lớn của mảnh vườn là:

   17,5 + 9 = 26,5 (m)

   Diện tích mảnh vườn đó là:

   (17,5 + 26,5) × 22 : 2 = 484 (m²)

   Diện tích đất để trồng xoài là:

   484 × 14 = 121 (m²)

   Diện tích đất để trồng cam là:

   484 − 121 = 363 (m²)

   Đáp số: 363m².

   Vậy đáp án đúng điền vào ô trống là 363.

   III. Bài tập vận dụng

   Câu 1: Một thửa ruộng hình thang có đáy bé bằng  đáy lớn, chiều cao bằng  đáy lớn. Biết đáy lớn hình thang là 260m. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần 0,75 giờ cho mỗi 100m2 đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?

   A. 76,05 giờ

   B. 101,4 giờ

   C. 180 giờ

   D. 202,8 giờ

   Đáp án
   

   Độ dài đáy bé của thửa ruộng đó là:

   260 × 35 = 156 (m)

   Chiều cao của thửa ruộng đó là:

   260 × 14 = 65 (m)

   Diện tích của thửa ruộng đó là:

   (156 + 260) × 652 = 13520 (m²)

   13520m2 gấp 100m2 số lần là:

   13520: 100 = 135,2 (lần)

   Bác Hùng cần dùng số giờ để làm sạch cỏ trên cả thửa ruộng đó là:

   0,75 × 135,2 = 101,4 (giờ)

   Đáp số: 101,4 giờ.

   Câu 2: Điền số thích hợp vào ô trống:

   Cho hình thang có độ dài hai đáy lần lượt là 15,6m và 9,5m. Nếu kéo dài đáy lớn thêm 1,75m thì diện tích tăng thêm 7m².

   Vậy diện tích hình thang ban đầu là  dm².

   Đáp án
   

   Theo bài ra ta có hình vẽ:

   

   Phần diện tích tăng thêm chính là diện tích của hình tam giác có đáy là 1,75m và chiều cao cũng chính là chiều cao của hình thang.

   Chiều cao của hình thang là:

   7 × 2 : 1,75 = 8 (m)

   Diện tích hình thang là:

   (15,6 + 9,5) × 8 : 2 = 100,4 (m²)

   100,4m² = 10040dm²

   Đáp số: 10040dm².

   Vậy đáp án đúng điền vào ô trống là 10040.

   Câu 3: Trong các hình sau, hình nào là hình thang?

   

   Đáp án
   

   Quan sát các hình đã cho ta thấy các hình thứ nhất, thứ ba và thứ tư có một cặp cạnh đối diện song song nên các hình đó là hình thang.

   B. Hình thang

   a) Định nghĩa

   

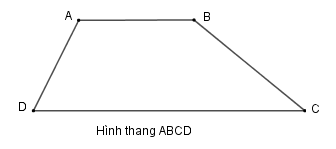
   Hình thang ABCD có:

   – Cạnh đáy AB và cạnh đáy DC. Cạnh bên AD và cạnh bên BC.

   – Hai cạnh đáy là hai cạnh đối diện song song.

   Hình thang có một cặp cạnh đối diện song song.

   Chú ý: Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.

   

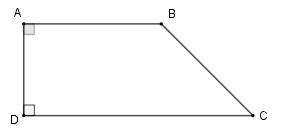
   b) Đường cao của hình thang

   
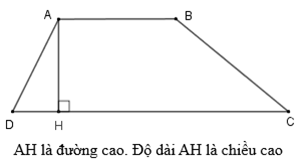
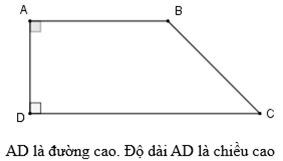
4. Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại I. Tìm các cặp tam giác có diện tích bằng nhau.
   
   

   Câu hỏi:
   

   Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại I. Tìm các cặp tam giác có diện tích bằng nhau.

   Trả lời:

   
   Ta có 3 cặp tam giác có diện tích bằng nhau là
   S _ADB = S_ABC (vì cùng đáy AB x chiều cao chia 2)
   S_ACD = S_BCD
   S_AID  = S_IBC
   Vì chúng đều là phần diện tích còn lại của 2 tam giác có diện tích bằng nhau và có chung 1 phần diện tích. (Tam giác  ICD hoặc AIB)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình thang ABCD có đáy nhỏ AB là 27 cm, đáy lớn CD là 48 cm. Nếu kéo dài đáy nhỏ thêm 5 cm thì diện tích của hình tăng 40 cm2. Tính diện tích hình thang đã cho.
   
   

   Câu hỏi:
   

   Cho hình thang ABCD có đáy nhỏ AB là 27 cm, đáy lớn CD là 48 cm. Nếu kéo dài đáy nhỏ thêm 5 cm thì diện tích của hình tăng 40 cm². Tính diện tích hình thang đã cho.

   Trả lời:

   

   ∆ CBE có :
   Đáy BE = 5 cm, chiều cao là chiều cao của hình thang ABCD . 
   Vậy chiều cao của hình thang ABCD
   là :  40 x 2 : 5 = 16 (cm)
    Diện tích hình thang ABCD là :
    (27 + 48) x 16 : 2 = 600 (cm2)
    

    

    
    

    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====