Tàu A cách cảng C một khoảng 3km và lệch hướng bắc 1 góc 47,45°. Tàu B cách cảng C một khoảng 5km và lệch hướng bắc một góc 112,90° (Hình 11). Khoảng cách giữa hai tàu là bao nhiêu ki – lô – mét (làm tròn kết quả đến hàng phần trăm).

Câu hỏi:

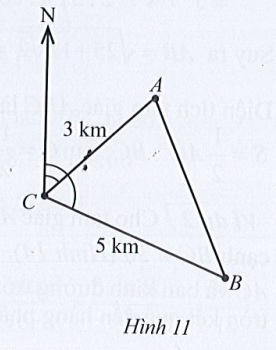
Tàu A cách cảng C một khoảng 3km và lệch hướng bắc 1 góc 47,45°. Tàu B cách cảng C một khoảng 5km và lệch hướng bắc một góc 112,90° (Hình 11). Khoảng cách giữa hai tàu là bao nhiêu ki – lô – mét (làm tròn kết quả đến hàng phần trăm).

Trả lời:

Lời giải
Theo đầu bài, ta có: \(\widehat {NCA} = 47,45^\circ \) và \(\widehat {NCB} = 112,9^\circ \)
⇒ \(\widehat {ACB} = \widehat {NCB} – \widehat {NCA} = 112,90^\circ – 47,45^\circ = 65,45^\circ \)
Xét tam giác ABC, có:
AB² = AC² + BC² – 2.AC.BC.cos\(\widehat {ACB}\)
⇔ AB² = 3² + 5² – 2.3.5.cos65,45°
⇔ AB² ≈ 21,54
⇔ AB ≈ 4,64
Vậy khoảng cách giữa hai tàu là 4,64 km.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho 0° < α < 180°. Chọn câu trả lời đúng. A. cosα < 0. B. sinα > 0. C. tanα < 0. D. cotα > 0.
   
   

   Câu hỏi:
   

   Cho 0° < α < 180°. Chọn câu trả lời đúng.
   A. cosα < 0.
   B. sinα > 0.
   C. tanα < 0.
   D. cotα > 0.

   Trả lời:

   Lời giải
   Đáp án đúng là B
   
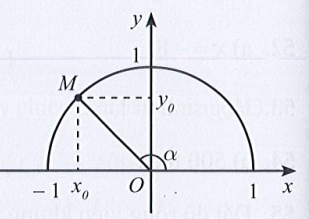
   Với 0° < α < 180°, ta có:
   – 1 < cosα < 1. Suy ra A sai.
   0 < sinα < 1. Suy ra B đúng.
   Do đó C và D sai.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho 0° < α, β < 180° và α + β = 180°. Chọn câu trả lời sai. A. sinα + sinβ = 0. B. cosα + cosβ = 0. C. tanα + tanβ = 0. D. cotα + cotβ = 0.
   
   

   Câu hỏi:
   

   Cho 0° < α, β < 180° và α + β = 180°. Chọn câu trả lời sai.
   A. sinα + sinβ = 0.
   B. cosα + cosβ = 0.
   C. tanα + tanβ = 0.
   D. cotα + cotβ = 0.

   Trả lời:

   Lời giải
   Đáp án đúng là A
   Ta có α + β = 180° nên ta có:
   sinα = sinβ ⇒ sinα + sinβ = sinα + sinα = 2sinα
   Vì 0° < α, β < 180° nên sinα ≠ 0.
   Do đó sinα + sinβ ≠ 0. Suy ra A sai.
   cosα = – cosβ ⇒ cosα + cosβ = 0. Suy ra B đúng.
   tanα = – tanβ ⇒ tanα + tanβ = 0. Suy ra C đúng.
   cotα = – cotβ ⇒ cotα + cotβ = 0. Suy ra D đúng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tính giá trị biểu thức T = sin225° + sin275° + sin2115° + sin2165°.
   
   

   Câu hỏi:
   

   Tính giá trị biểu thức T = sin²25° + sin²75° + sin²115° + sin²165°.

   Trả lời:

   Lời giải
   T = sin²25° + sin²75° + sin²115° + sin²165°
   = sin²25° + sin²75° + sin²75° + sin²25°
   = 2sin²25° + 2sin²75°
   = 2sin²25° + 2cos²25°
   = 2(sin²25° + cos²25°)
   = 2.1 = 2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tanα = – 2. Tính giá trị biểu thức P = \(\frac{{{\rm{cos}}\alpha + 3\sin \alpha }}{{\sin \alpha + 3\cos \alpha }}\).
   
   

   Câu hỏi:
   

   Cho tanα = – 2. Tính giá trị biểu thức P = \(\frac{{{\rm{cos}}\alpha + 3\sin \alpha }}{{\sin \alpha + 3\cos \alpha }}\).

   Trả lời:

   Lời giải
   Ta có: tanα = – 2 thỏa mãn cosα ≠ 0
   P = \(\frac{{{\rm{cos}}\alpha + 3\sin \alpha }}{{\sin \alpha + 3\cos \alpha }} = \frac{{\frac{{{\rm{cos}}\alpha }}{{{\rm{cos}}\alpha }} + 3\frac{{\sin \alpha }}{{{\rm{cos}}\alpha }}}}{{\frac{{\sin \alpha }}{{{\rm{cos}}\alpha }} + 3\frac{{\cos \alpha }}{{{\rm{cos}}\alpha }}}} = \frac{{1 + 3\tan \alpha }}{{\tan \alpha + 3}} = \frac{{1 + 3.\left( { – 2} \right)}}{{ – 2 + 3}} = \frac{{ – 5}}{1} = – 5\).
   Vậy với tanα = – 2 thì P = – 5.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác ABC có AB = 6, AC = 8, \(\widehat A = 100^\circ \). Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
   
   

   Câu hỏi:
   

   Cho tam giác ABC có AB = 6, AC = 8, \(\widehat A = 100^\circ \). Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).

   Trả lời:

   Lời giải
   Xét tam giác ABC, có:
   BC² = AB² + AC² – 2.AB.AC.cosA (định lí cos)
   ⇔ BC² = 6² + 8² – 2.6.8.cos100°
   ⇔ BC² ≈ 116,7
   ⇔ BC ≈ 10,8.
   Áp dụng định lí sin trong tam giác ABC, ta có:
   \(\frac{{BC}}{{\sin A}} = 2R\)
   ⇔ \(\frac{{10,8}}{{\sin 100}} = 2R\)
   ⇔ \(\frac{{10,8}}{{2\sin 100^\circ }} = R\)
   ⇔ R ≈ 5,5.
   Vậy BC ≈ 10,8 và R ≈ 5,5.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====