Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39). Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho MK2 – MO2 = 1 là một đường parabol.

Câu hỏi:

Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).

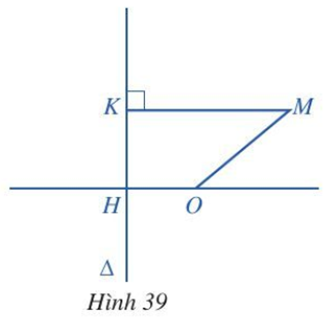
Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho MK² – MO² = 1 là một đường parabol.

Trả lời:

Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.
Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).
Khi đó:
MK² – MO² = 1
$\iff${[x – (–1)]² + (y – y)²} – [(0 – x)² + (0 – y)²] = 1
$\iff${(x + 1)² + 0²} – [x² + y²] = 1
$\iff$(x² + 2x +1) – (x² + y²) = 1
$\iff$ 2x +1 – y² = 1
$\iff$ y² = 2x.
Vậy tập hợp các điểm M là parabol có phương trình y² = 2x.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

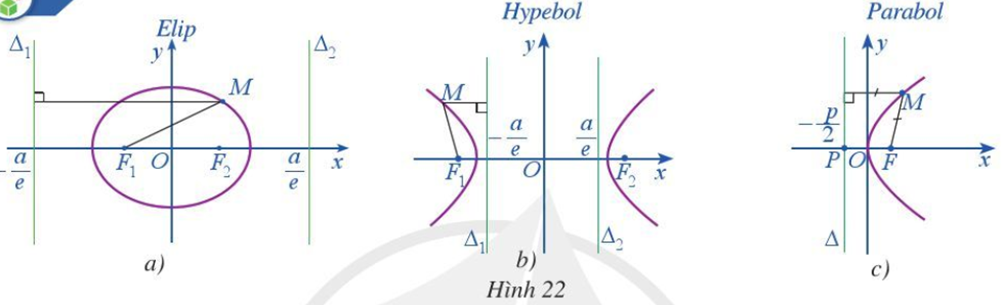
1. Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
   
   

   Câu hỏi:
   

   Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
   

   Trả lời:

   – Với mọi điểm M thuộc elip (E): $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b >0), ta luôn có $\frac{MF}{d(M,\Delta )}=e$ (0 < e < 1), trong đó F là một trong hai tiêu điểm F₁, F₂ và Δ là đường chuẩn ứng với tiêu điểm F.
   – Với mọi điểm M thuộc hypebol (H): $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0), ta luôn có $\frac{MF}{d(M,\Delta )}=e$ (e > 1), trong đó F là một trong hai tiêu điểm F₁, F₂ và Δ là đường chuẩn ứng với tiêu điểm F.
   – Với mọi điểm M thuộc parabol (P): y² = 2px (p > 0), ta luôn có $\frac{MF}{d(M,\Delta )}=1$, trong đó F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm F.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình chữ nhật ABCD với bốn đỉnh A(–4; 3), B(4; 3), C(4; –3), D(–4; –3). a) Viết phương trình chính tắc của elip nhận ABCD là hình chữ nhật cơ sở. Vẽ elip đó. b) Viết phương trình chính tắc của hypebol nhận ABCD là hình chữ nhật cơ sở. Vẽ hypebol đó.
   
   

   Câu hỏi:
   

   Cho hình chữ nhật ABCD với bốn đỉnh A(–4; 3), B(4; 3), C(4; –3), D(–4; –3).
   a) Viết phương trình chính tắc của elip nhận ABCD là hình chữ nhật cơ sở. Vẽ elip đó.
   b) Viết phương trình chính tắc của hypebol nhận ABCD là hình chữ nhật cơ sở. Vẽ hypebol đó.

   Trả lời:

   Gọi M, N lần lượt là trung điểm của AB, BC.
   Toạ độ của M là $\left(x_M;y_M\right)=\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right)=\left(\frac{-4+4}{2};\frac{3+3}{2}\right)=\left(0;3\right).$
   Toạ độ của N là $\left(x_N;y_N\right)=\left(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2}\right)=\left(\frac{4+4}{2};\frac{3+\left(-3\right)}{2}\right)=\left(4;0\right).$
   a) Gọi phương trình chính tắc của elip cần tìm là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).
   Vì ABCD là hình chữ nhật cơ sở của elip nên M, N là hai đỉnh của elip.
   Lại có: M(0; 3) $\Rightarrow$ b = 3, N(4; 0) $\Rightarrow$ a = 4.
   Vậy phương trình chính tắc của elip cần tìm là $\frac{x^2}{16}+\frac{y^2}{9}=1.$ 
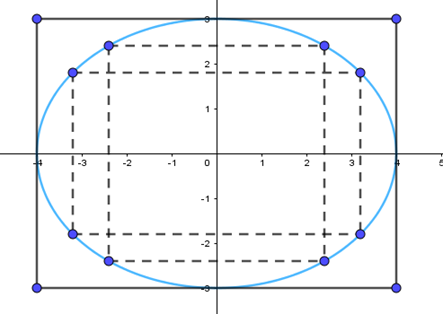
   +) Vẽ elip:
   Ta thấy a = 4, b = 3. Toạ độ các đỉnh của elip là (–4; 0), (5; 0), (0; – 3), (0; 3).
   Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –4, x = 4, y = –3, y = 3.
   Bước 2. Tìm một số điểm cụ thể thuộc elip, chẳng hạn ta thấy điểm $X\left(\frac{12}{5};\frac{12}{5}\right)$ và điểm $Y\left(\frac{16}{5};\frac{9}{5}\right)$ thuộc (E). Do đó các điểm $X_1\left(\frac{12}{5};-\frac{12}{5}\right),$ $X_2\left(-\frac{12}{5};\frac{12}{5}\right),$ $X_3\left(-\frac{12}{5};-\frac{12}{5}\right)$, $Y_1\left(\frac{16}{5};-\frac{9}{5}\right),$ $Y_2\left(-\frac{16}{5};\frac{9}{5}\right),$$Y_3\left(-\frac{16}{5};-\frac{9}{5}\right)$ cũng thuộc (E).
   Bước 3. Vẽ đường elip (E) đi qua các điểm cụ thể trên, nằm ở phía trong hình chữ nhật cơ sở và tiếp xúc với các cạnh của hình chữ nhật cơ sở tại bốn đỉnh của (E) là
   (–4; 0), (4; 0), (0; –3), (0; 3).
   

   Gọi phương trình chính tắc của hypebol cần tìm là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).
   Vì M(0; 3) và N(4;0) là trung điểm các cạnh của hình chữ nhật cơ sở nên a = 4, b = 3.
   Vậy phương trình chính tắc của hypebol cần tìm là $\frac{x^2}{16}-\frac{y^2}{9}=1.$ 
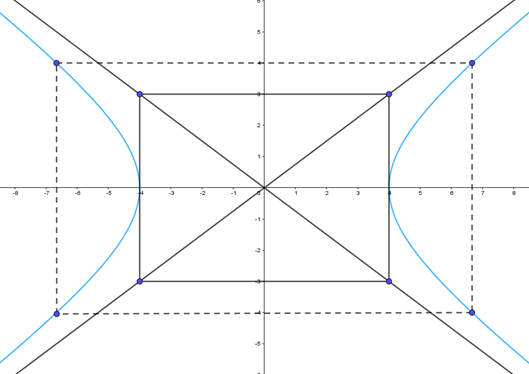
   +) Vẽ hypebol:
   Ta thấy a = 4, b = 3. (H) có các đỉnh là (–4; 0), (4; 0).
   Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –4, x = 4, y = –3, y = 3.
   Bước 2. Vẽ hai đường chéo của hình chữ nhật cơ sở.
   Tim một số điểm cụ thể thuộc hypebol, chẳng hạn ta thấy điểm $X\left(\frac{20}{3};4\right)$ thuộc (H). Do đó các điểm $X_1\left(\frac{20}{3};-4\right),X_2\left(-\frac{20}{3};4\right),X_3\left(-\frac{20}{3};-4\right)$ thuộc (H).
   Bước 3. Vẽ đường hypebol bên ngoài hình chữ nhật cơ sở; nhánh bên trái tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm (–4; 0) và đi qua X₂, X₃; nhánh bên phải tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm (4; 0) và đi qua X, X₁. Vẽ các điểm thuộc hypebol càng xa gốc toạ độ thì càng sát với đường tiệm cận. Hypebol nhận gốc toạ độ là tâm đối xứng và hai trục toạ độ là hai trục đối xứng.
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các trục, toạ độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó. a) x2100+y264=1; b) x236−y264=1.
   
   

   Câu hỏi:
   

   Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các trục, toạ độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó.
   a) $\frac{x^2}{100}+\frac{y^2}{64}=1$;
   b) $\frac{x^2}{36}-\frac{y^2}{64}=1$.

   Trả lời:

   a) Đây là đường elip.
   Ta có a = 10, b = 8 $\Rightarrow c=\sqrt{a^2-b^2}=6.$
   Độ dài trục lớn là 2a = 20, độ dài trục bé là 2b = 16.
   Toạ độ các tiêu điểm là F₁(–6; 0) và F₂(6; 0).
   Tiêu cự là 2c = 12.
   Tâm sai là $\Rightarrow c=\sqrt{a^2+b^2}=10.$
   b) Đây là đường hypebol.
   Ta có a = 6, b = 8 $\Rightarrow c=\sqrt{a^2+b^2}=10.$
   Độ dài trục thực là 2a = 12, độ dài trục ảo là 2b = 16.
   Toạ độ các tiêu điểm là F₁(–10; 0) và F₂(10; 0).
   Tiêu cự là 2c = 20.
   Tâm sai là $e=\frac{c}{a}=\frac{10}{6}=\frac{5}{3}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
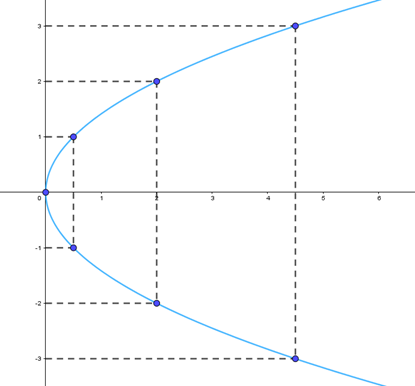
4. Cho parabol có phương trình chính tắc y2 = 2x. Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.
   
   

   Câu hỏi:
   

   Cho parabol có phương trình chính tắc y² = 2x. Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.

   Trả lời:

   Ta có: 2p = 2 $\Rightarrow p=1\Rightarrow \frac{p}{2}=\frac{1}{2}.$
   Vậy tiêu điểm của parabol là $F\left(\frac{1}{2};0\right)$ và đường chuẩn của parabol là $x=-\frac{1}{2}.$
   Vẽ parabol:
   Bước 1. Lập bảng giá trị

   x

   0

   0,5

   0,5

   2

   2

   4,5

   4,5

   y

   0

   –1

   1

   –2

   2

   –3

   3

   Chú ý rằng ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau.
   Bước 2. Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị.
   Bước 3. Vẽ parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2.
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm A(–3; 1), B(2; 8), C(0; 3). a) Tính các tỉ số sau: AFd(A,Δ),BFd(B,Δ),CFd(C,Δ). b) Hỏi mỗi điểm A, B, C lần lượt nằm trên loại đường conic nào nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó?
   
   

   Câu hỏi:
   

   Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm A(–3; 1), B(2; 8), C(0; 3).
   a) Tính các tỉ số sau: $\frac{AF}{d(A,\Delta )},\frac{BF}{d(B,\Delta )},\frac{CF}{d(C,\Delta )}$.
   b) Hỏi mỗi điểm A, B, C lần lượt nằm trên loại đường conic nào nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó?

   Trả lời:

   a) Ta viết lại phương trình đường thẳng Δ: x + 0 . y + 5 = 0. Khi đó
   $\frac{AF}{d(A,\Delta )}=\frac{\sqrt{{\left(-4-\left(-3\right)\right)}^2+{\left(0-1\right)}^2}}{\frac{\left|-3+0.1+5\right|}{\sqrt{1^2+0^2}}}=\frac{\sqrt{2}}{2};$
   $\frac{BF}{d(B,\Delta )}=\frac{\sqrt{{\left(-4-2\right)}^2+{\left(0-8\right)}^2}}{\frac{\left|2+0.8+5\right|}{\sqrt{1^2+0^2}}}=\frac{10}{7};$
   $\frac{CF}{d(C,\Delta )}=\frac{\sqrt{{\left(-4-0\right)}^2+{\left(0-3\right)}^2}}{\frac{\left|0+0.3+5\right|}{\sqrt{1^2+0^2}}}=1.$
   b)
   – Vì $\frac{AF}{d(A,\Delta )}=\frac{\sqrt{2}}{2}<1$ nên A nằm trên elip nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó.
   – Vì $\frac{BF}{d(B,\Delta )}=\frac{10}{7}>1$ nên A nằm trên hypebol nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó.
   – Vì $\frac{CF}{d(C,\Delta )}=1$ nên A nằm trên parabol nhận F là tiêu điểm và Δ là đường chuẩn.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====