Cho tam giác ABC. Khẳng định nào sau đây là đúng? a) A. S=abc4r. B. r=2Sa+b+c. C. a2 = b2 + c2 + 2bc.cosA. D. S = r(a + b + c). b) A. sinA = sin(B + C). B. cosA = cos(B + C). C. cosA > 0. D. sinA ≤ 0

Câu hỏi:

Cho tam giác ABC. Khẳng định nào sau đây là đúng?
a)
A. $S=\frac{abc}{4r}.$
B. $r=\frac{2S}{a+b+c}.$
C. a² = b² + c² + 2bc.cosA.
D. S = r(a + b + c).
b)
A. sinA = sin(B + C).
B. cosA = cos(B + C).
C. cosA > 0.
D. sinA ≤ 0

Trả lời:

a) Ta có: $S=pr=\frac{abc}{4R}=\frac{\left(a+b+c\right)r}{2}$. Do đó A,D sai.
Theo định lí cos, ta có: a² = b² + c² – 2bc.cosA. Do đó C sai.
Ta có: $S=\frac{\left(a+b+c\right)r}{2}\Rightarrow r=\frac{2S}{a+b+c}$. Do đó B đúng.
Chọn B
b) Ta có: $\widehat{A}+\widehat{B}+\widehat{C}={180}^0\Rightarrow \widehat{A}={180}^0-\left(\widehat{B}+\widehat{C}\right)$
$\sin \widehat{A}=\sin \left[{180}^0-\left(\widehat{B}+\widehat{C}\right)\right]=\sin \left(\widehat{B}+\widehat{C}\right)$. Do đó A đúng.
$co\mathrm{s}\widehat{A}=co\mathrm{s}\left[{180}^0-\left(\widehat{B}+\widehat{C}\right)\right]=-co\mathrm{s}\left(\widehat{B}+\widehat{C}\right)$. Do đó B sai.
Ta có: cosA > 0 khi 0⁰ < $\widehat{A}$ < 90⁰. Do đó C sai.
Trong một tam giác, ta có: $0^0\le \widehat{A}\le {180}^0$ ⇒ sin A ≥ 0. Do đó D đúng.
Chọn A

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tam giác ABC có B^=1350. Khẳng định nào sau đây là đúng? a) A. S=12ca.           B. S=−24ac.  C. S=24bc. D. S=24ca. b) A. R=asinA. B. R=22b. C. R=22c. D. R=22a. c) A. a2=b2+c2+2ab. B. bsinA=asinB. C. sinB=−22. D. b2 = c2 + a2 – 2ca.cos1350.
   
   

   Câu hỏi:
   

   Cho tam giác ABC có $\widehat{B}={135}^0$. Khẳng định nào sau đây là đúng?
   a)
   A. $S=\frac{1}{2}ca.$          
   B. $S=\frac{-\sqrt{2}}{4}ac.$ 
   C. $S=\frac{\sqrt{2}}{4}bc.$
   D. $S=\frac{\sqrt{2}}{4}ca.$
   b)
   A. $R=\frac{a}{\sin A}.$
   B. $R=\frac{\sqrt{2}}{2}b.$
   C. $R=\frac{\sqrt{2}}{2}c.$
   D. $R=\frac{\sqrt{2}}{2}a.$
   c)
   A. $a^2=b^2+c^2+\sqrt{2}ab$.
   B. $\frac{b}{\sin A}=\frac{a}{\sin B}.$
   C. $\sin B=\frac{-\sqrt{2}}{2}.$
   D. b² = c² + a² – 2ca.cos135⁰.

   Trả lời:

   

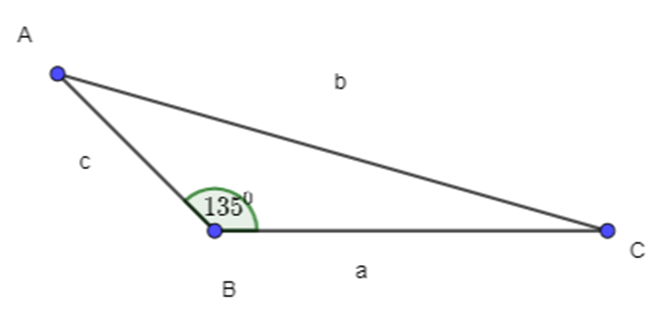
   a) Diện tích tam giác ABC: $S=\frac{1}{2}.a.c.\sin B=\frac{1}{2}a.c.\sin {135}^0=\frac{\sqrt{2}}{4}ac$.
   Chọn D.
   b) Ta có: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$(định lí sin)
   $\Rightarrow R=\frac{b}{2\sin B}=\frac{b}{2\sin {135}^0}=\frac{b}{\sqrt{2}}=\frac{\sqrt{2}}{2}b.$
   Chọn B.
   c) Theo định lí cos, ta có:
   b² = a² + c² – 2ac.cosB = a² + c² – 2ac.cos135⁰.
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tính giá trị các biểu thức sau: a) M = sin450.cos450 + sin300; b) ​N=sin600.cos300+12sin450.cos450; c) P = 1 + tan2600; d) Q=1sin21200−cot1200.
   
   

   Câu hỏi:
   

   Tính giá trị các biểu thức sau:
   a) M = sin45⁰.cos45⁰ + sin30⁰;
   b) $\text{}N=\sin {60}^0.cos{30}^0+\frac{1}{2}\sin {45}^0.cos{45}^0$;
   c) P = 1 + tan²60⁰;
   d) $Q=\frac{1}{{\sin }^2{120}^0}-\cot {120}^0.$

   Trả lời:

   a) M = sin45⁰.cos45⁰ + sin30^{0
   $=\frac{\sqrt{2}}{2}.\frac{\sqrt{2}}{2}+\frac{1}{2}=\frac{1}{2}+\frac{1}{2}=1$}
   b) $\text{}N=\sin {60}^0.cos{30}^0+\frac{1}{2}\sin {45}^0.cos{45}^0$
   = $\frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}+\frac{1}{2}.\frac{\sqrt{2}}{2}.\frac{\sqrt{2}}{2}=\frac{3}{4}+\frac{1}{4}=1$
   c) P = 1 + tan²60^{0
   $=1+{\left(\sqrt{3}\right)}^2=1+3=4$}
   d) $Q=\frac{1}{{\sin }^2{120}^0}-\cot {120}^0$
   $=\frac{1}{{\sin }^2{60}^0}+\cot {60}^0$
   $=\frac{4}{3}+\frac{1}{\sqrt{3}}=\frac{4+\sqrt{3}}{3}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC có B^=600,C^=450,AC = 10. Tính a, R, S, r.
   
   

   Câu hỏi:
   

   Cho tam giác ABC có $\widehat{B}={60}^0,\widehat{C}={45}^0,$AC = 10. Tính a, R, S, r.

   Trả lời:

   

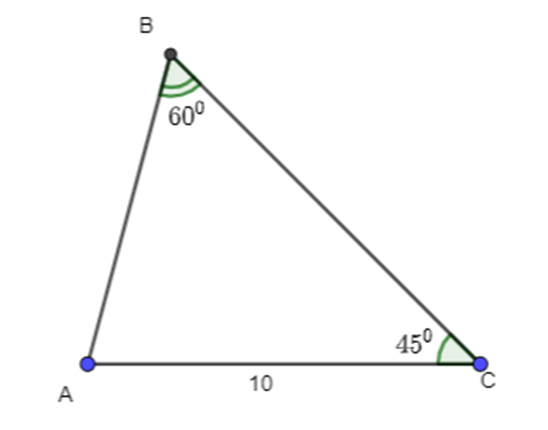
   Xét ΔABC, có:
   Ta có: $\widehat{A}={180}^0-\widehat{B}-\widehat{C}={180}^0-{60}^0-{45}^0={75}^0.$
   $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ (định lí sin)
   $\Rightarrow \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{10}{\sin {60}^0}=\frac{10}{\frac{\sqrt{3}}{2}}=\frac{20}{\sqrt{3}}\Rightarrow a=\frac{20}{\sqrt{3}}\sin A=\frac{20}{\sqrt{3}}.\sin {75}^0=11,15$
   $\Rightarrow 2R=\frac{b}{\sin B}=\frac{20}{\sqrt{3}}\iff R=\frac{10}{\sqrt{3}}$..
   Diện tích tam giác ABC là: $S=\frac{1}{2}.b.a.\sin C=\frac{1}{2}\mathrm{.10.11},15.\sin {45}^0\approx 39,42$ (đvdt)
   $\Rightarrow \frac{c}{\sin C}=\frac{b}{\sin B}=\frac{20}{\sqrt{3}}\Rightarrow c=\frac{20}{\sqrt{3}}\sin C=\frac{20}{\sqrt{3}}.\sin {45}^0=\frac{10\sqrt{6}}{3}$
   Ta có: $S=pr=\frac{\left(a+b+c\right)r}{2}\Rightarrow r=\frac{2S}{a+b+c}=\frac{2.39,42}{11,15+10+\frac{10\sqrt{6}}{3}}=2,69$
   Vậy a = 11,15; $R=\frac{10}{\sqrt{3}},c=\frac{10\sqrt{6}}{3},$ r = 2,69.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC có trung tuyến AM. Chứng minh rằng: a) cosAMB^+cosAMC^=0; b) MA2 + MB2 – AB2 = 2MA.MB.cosAMB^ và MA2 + MC2 – AC2 = 2MA.MC.cosAMC^; c) MA2=2AB2+AC2−BC24 (công thức đường trung tuyến).
   
   

   Câu hỏi:
   

   Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
   a) $cos\widehat{AMB}+cos\widehat{AMC}=0;$
   b) MA² + MB² – AB² = 2MA.MB.cos$\widehat{AMB}$ và MA² + MC² – AC² = 2MA.MC.cos$\widehat{AMC}$;
   c) $M{A}^2=\frac{2\left(A{B}^2+A{C}^2\right)-B{C}^2}{4}$ (công thức đường trung tuyến).

   Trả lời:

    
   

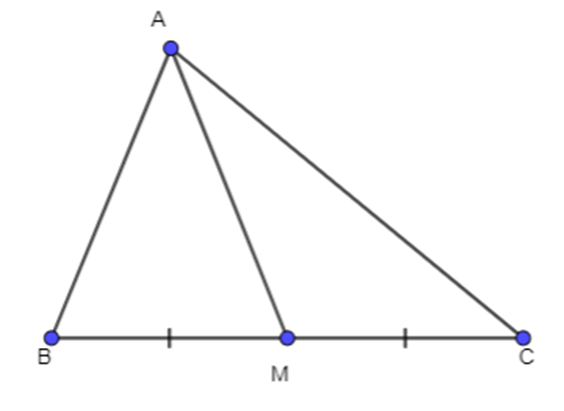
   a) $cos\widehat{AMB}+cos\widehat{AMC}=0$
   Ta có: $\widehat{AMB}+\widehat{AMC}={180}^0$
   $\widehat{AMC}={180}^0-\widehat{AMB}$
   $cos\widehat{AMB}=-cos\left({180}^0-\widehat{AMB}\right)=-cos\widehat{AMC}$
   $\Rightarrow cos\widehat{AMB}+cos\widehat{AMC}=-cos\widehat{AMC}+cos\widehat{AMC}=0$
   b) Xét ΔAMB, ta có:
   AB² = MA² + MB² – 2MA.MB.cos$\widehat{AMB}$ 
   ⇔ MA² + MB² – AB² = 2MA.MB.cos $\widehat{AMB}$(1)
   Xét ΔAMC, ta có:
   AC² = MA² + MC² – 2MA.MC.cos $\widehat{AMC}$
   ⇔ MA² + MC² – AC² = 2MA.MC.cos $\widehat{AMC}$ (2)
   c) Cộng vế với vế của (1) với (2), ta được:
   MA² + MB² – AB² + MA² + MC² – AC²
   = 2MA.MB.cos $\widehat{AMB}$ + 2MA.MC.cos $\widehat{AMC}$ 
   $\iff 2M{A}^2+\frac{B{C}^2}{4}–A{B}^2+\frac{B{C}^2}{4}–A{C}^2=2MA.\frac{BC}{2}.cos\widehat{AMB} +2MA.\frac{BC}{2}.cos\widehat{AMC}$
   (Vì $MB=MC=\frac{BC}{2}$)
   $\iff 2M{A}^2+\frac{B{C}^2}{2}–A{B}^2–A{C}^2=2MA.\frac{BC}{2}.\left(cos\widehat{AMB} +cos\widehat{AMC}\right)$
   $\iff 2M{A}^2+\frac{B{C}^2}{2}–A{B}^2–A{C}^2=\text{ 0}$ (vì $cos\widehat{AMB} +cos\widehat{AMC}=0$)
   $\iff 2M{A}^2=\frac{2A{B}^2+2A{C}^2-B{C}^2}{2}$
   $\iff M{A}^2=\frac{2\left(A{B}^2+A{C}^2\right)-B{C}^2}{4}$ (công thức đường trung tuyến).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác ABC. Chứng minh rằng: a) Nếu góc A nhọn thì b2 + c2 > a2; b) Nếu góc A tù thì b2 + c2 < a2; c) Nếu góc A vuông thì b2 + c2 = a2.
   
   

   Câu hỏi:
   

   Cho tam giác ABC. Chứng minh rằng:
   a) Nếu góc A nhọn thì b² + c² > a²;
   b) Nếu góc A tù thì b² + c² < a²;
   c) Nếu góc A vuông thì b² + c² = a².

   Trả lời:

   Xét ΔABC, có:
   Theo định lí cos, ta có: a² = b² + c² – 2bc.cosA
   a) Nếu góc A nhọn thì cosA > 0 ⇒ 2bccosA > 0 ⇒ – 2bccosA < 0
   Do đó: a² = b² + c² – 2bc.cosA < b² + c²
   Vậy b² + c² > a²
   b) Nếu góc A tù thì cosA > 0 ⇒ 2bccosA < 0 ⇒ – 2bccosA > 0
   Do đó: a² = b² + c² – 2bc.cosA > b² + c²
   Vậy b² + c² < a².
   c) Nếu góc A vuông thì cosA = 0 ⇒ 2bccosA = 0
   Do đó: a² = b² + c² – 2bc.cosA = b² + c²
   Vậy b² + c² = a².

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====