Cho S là một điểm không thuộc mặt phẳng chứa hình bình hành ABCD. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

Câu hỏi:

Cho S là một điểm không thuộc mặt phẳng chứa hình bình hành ABCD. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

Trả lời:

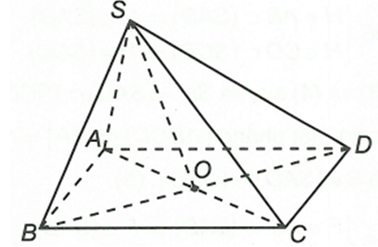
Ta có $S\in \left(SAC\right)\cap \left(SBD\right)\left(1\right)$
Trong mặt phẳng (ABCD) có $AC\cap BD=\left\{O\right\}$
Lại có
$\left\{\begin{array}{l}O\in AC\subset \left(ASC\right)\Rightarrow O\in \left(SAC\right)\\ O\in BD\subset \left(SBD\right)\Rightarrow O\in \left(ABD\right)\end{array}\right.\Rightarrow O\in \left(SAC\right)\cap \left(ABD\right)\left(2\right)$

Từ (1) và (2) suy ra $SO=\left(SAC\right)\cap \left(SBD\right)$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong mặt phẳng αcho tức giác ABCD có các cặp cạnh đối không song song và S∉α . Xác định giao tuyến của các cặp mặt phẳng sau đây: a) SAC và SBD
   
   

   Câu hỏi:
   

   Trong mặt phẳng $\left(\alpha \right)$cho tức giác ABCD có các cặp cạnh đối không song song và $S\notin \left(\alpha \right)$ . Xác định giao tuyến của các cặp mặt phẳng sau đây:
   a) $\left(SAC\right)$ và $\left(SBD\right)$

   Trả lời:

   

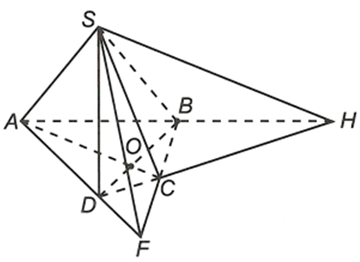
   a) Trong mặt phẳng (ABCD) gọi $\left\{O\right\}=AC\cap DB$
   Ta có $S\in \left(SAC\right)\cap \left(SBD\right)\left(1\right)$
   Lại có
   $\left\{\begin{array}{l}O\in AC\subset \left(SAC\right)\Rightarrow O\in \left(SAC\right)\\ O\in BD\subset \left(SBD\right)\Rightarrow O\in \left(SBD\right)\end{array}\right.\Rightarrow O\in \left(SAC\right)\cap \left(SBD\right)\left(2\right)$
   Từ (1) và (2) suy ra $SO=\left(SAC\right)\cap \left(SBD\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. b) (SAB) và (SCD)
   
   

   Câu hỏi:
   

   b) (SAB) và (SCD)

   Trả lời:

   b) Trong mặt phẳng (ABCD) gọi $\left\{H\right\}=AB\cap CD$
   Ta có $S\in \left(SAB\right)\cap \left(SCD\right)$
   Lại có $\left\{\begin{array}{l}H\in AB\subset \left(SAB\right)\Rightarrow H\in \left(SAB\right)\\ H\in CD\subset \left(SCD\right)\Rightarrow H\in \left(SCD\right)\end{array}\right.\Rightarrow H\in \left(SAB\right)\cap \left(SCD\right)\left(4\right)$
   Từ (3) và (4) suy ra $SH=\left(SAB\right)\cap \left(SCD\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. c) (SAD) và (SBC)
   
   

   Câu hỏi:
   

   c) (SAD) và (SBC)

   Trả lời:

   c) Trong mặt phẳng (ABCD) gọi $\left\{F\right\}=AD\cap CB$
   Ta có $S\in \left(SAD\right)\cap \left(SBC\right)\left(5\right)$
   Lại có $\left\{\begin{array}{l}F\in AD\subset \left(SAD\right)\Rightarrow F\in \left(SAD\right)\\ F\in CB\subset \left(SBC\right)\Rightarrow F\in \left(SBC\right)\end{array}\right.\Rightarrow F\in \left(SAD\right)\cap \left(SBC\right)\left(6\right)$
   Từ (5) và (6) suy ra $SF=\left(SAD\right)\cap \left(SBC\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho bốn điểm A, B, C, D không cùng thuộc một mặt phẳng. Trên các đoạn thẳng AB, AC, BD lần lượt lấy các điểm M, N, P sao cho MN không song song với BC. Tìm giao tuyến của (BCD) và (MNP)
   
   

   Câu hỏi:
   

   Cho bốn điểm A, B, C, D không cùng thuộc một mặt phẳng. Trên các đoạn thẳng AB, AC, BD lần lượt lấy các điểm M, N, P sao cho MN không song song với BC. Tìm giao tuyến của (BCD) và (MNP)

   Trả lời:

   

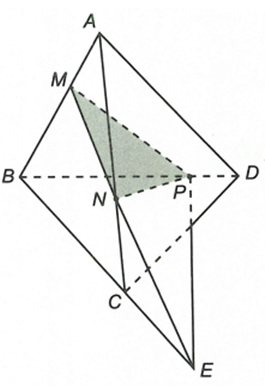
   Trong mặt phẳng (ABC) gọi $\left\{E\right\}=MN\cap BC$
   Ta thấy $P\in \left(BCD\right)\cap \left(MNP\right) \left(1\right)$
   Lại có $\left\{\begin{array}{l}E\in MN\subset \left(MNP\right)\Rightarrow E\in \left(MNP\right)\\ E\in BC\subset \left(BCD\right)\Rightarrow E\in \left(BCD\right)\end{array}\right.\Rightarrow E\in \left(MNP\right)\cap \left(BCD\right) \left(2\right)$
   Từ (1) và (2) suy ra $PE=\left(MNP\right)\cap \left(BCD\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho bốn điểm A, B, C, D không đồng phẳng. Trên hai đoạn thẳng AB, AC lần lượt lấy các điểm M, N sao cho AMBM=1 và ANNC=2. Tìm giao tuyến của (DMN) và (BCD).
   
   

   Câu hỏi:
   

   Cho bốn điểm A, B, C, D không đồng phẳng. Trên hai đoạn thẳng AB, AC lần lượt lấy các điểm M, N sao cho $\frac{AM}{BM}=1$ và $\frac{AN}{NC}=2$. Tìm giao tuyến của (DMN) và (BCD).

   Trả lời:

   

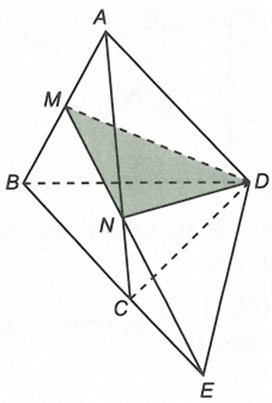
   Trong tam giác  có
   $\left\{\begin{array}{l}\frac{AM}{BM}=1\\ \frac{AN}{NC}=2\end{array}\right.\Rightarrow \frac{AM}{BM}\ne \frac{AN}{NC}$

   Nên MN và BC không song song theo định lý Ta-lét.
   Trong mặt phẳng (ABC) gọi $\left\{H\right\}=MN\cap BC$
   Ta thấy $D\in \left(BCD\right)\cap \left(DMN\right)$    (1)
   Lại có $\left\{\begin{array}{l}H\in MN\subset \left(DMN\right)\Rightarrow H\in \left(DMN\right)\\ H\in BC\subset \left(BCD\right)\Rightarrow H\in \left(BCD\right)\end{array}\right.$
   $\Rightarrow H\in \left(DMN\right)\cap \left(BCD\right) \left(2\right)$

   Từ (1) và (2) suy ra $DH=\left(DMN\right)\cap \left(BCD\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====