Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau : a) x+y−3≥0x≥0y≥0; b) x−2y−2y−x

Câu hỏi:

Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau :
a) $\left\{\begin{array}{c}x+y-3\ge 0\\ x\ge 0\\ y\ge 0;\end{array}\right.$
b) $\left\{\begin{array}{c}x-2y<0\\ x+3y>-2\\ y-x<3;\end{array}\right.$
c) $\left\{\begin{array}{c}x\ge 1\\ x\le 4\\ x+y-5\le 0\\ y\ge 0.\end{array}\right.$

Trả lời:

a) Hệ bất phương trình $\left\{\begin{array}{c}x+y-3\ge 0\\ x\ge 0\\ y\ge 0;\end{array}\right.$
Biểu diễn miền nghiệm của từng bất phương trình trên mặt phẳng Oxy.
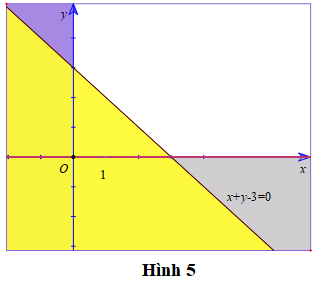
– Xác định miền nghiệm D₁ của bất phương trình x + y – 3 ≥ 0:
Lấy điểm O(0; 0) không thuộc đường thẳng d: x + y – 3 = 0, ta có: 0 + 0 – 3 = -3 < 0. Do đó miền nghiệm của bất phương trình x + y – 3 ≥ 0 là nửa mặt phẳng có bờ là đường thẳng d₁ (kể cả đường thẳng d₁) và không chứa gốc tọa độ O(0; 0) (như hình 5)
– Xác định miền nghiệm D₂ của bất phương trình x ≥ 0 là nửa mặt phẳng bên phải trục Oy và kể cả bờ Oy (như hình 5).
– Xác định miền nghiệm D₃ của bất phương trình y ≥ 0 là nửa mặt phẳng bên trên trục Ox và kể cả bờ Ox (như hình 5).
Vậy, miền không tô màu (bao gồm cả các bờ) trong hình 5 là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

b) Hệ bất phương trình $\left\{\begin{array}{c}x-2y<0\\ x+3y>-2\\ y-x<3;\end{array}\right.$
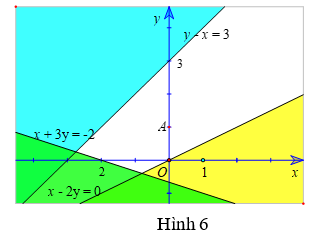
– Xác định miền nghiệm D₁ của bất phương trình x – 2y < 0:
Lấy điểm A(0; 1) không thuộc đường thẳng d₁: x – 2y = 0, ta có: 0 – 2.1 = -2 < 0. Do đó miền nghiệm D₁ là nửa mặt phẳng có bờ là đường thẳng d₁ (không kể đường thẳng d₁) và chứa điểm A (0; 1) (như hình 6).
– Xác định miền nghiệm D₂ của bất phương trình x + 3y > -2:
Lấy điểm O(0; 0) không thuộc đường thẳng d₂: x + 3y = – 2, ta có: 0 + 3.0 = 0 > – 2. Do đó miền nghiệm D₂ là nửa mặt phẳng bờ là đường thẳng d₂ (không kể đường thẳng d₂) và chứa gốc tọa độ O (như hình 6).
– Xác định miền nghiệm D₃ của bất phương trình y – x < 3:
Lấy điểm O(0; 0) không thuộc đường thẳng d₂: x + 3y = – 2, ta có: 0 + 3.0 = 0 > – 2.
Miền nghiệm của bất phương trình y – x < 3 là nửa mặt phẳng bờ là đường thẳng y – x = 3 (không kể bờ) và chứa gốc tọa độ O (như hình 6)
Vậy, miền không tô màu (không bao gồm cả các bờ) trong hình 6 là phần giao các miền nghiệm của các bất phương trình trong hệ và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

c) Hệ bất phương trình $\left\{\begin{array}{c}x\ge 1\\ x\le 4\\ x+y-5\le 0\\ y\ge 0.\end{array}\right.$
Biểu diễn miền nghiệm của từng bất phương trình trên mặt phẳng Oxy.
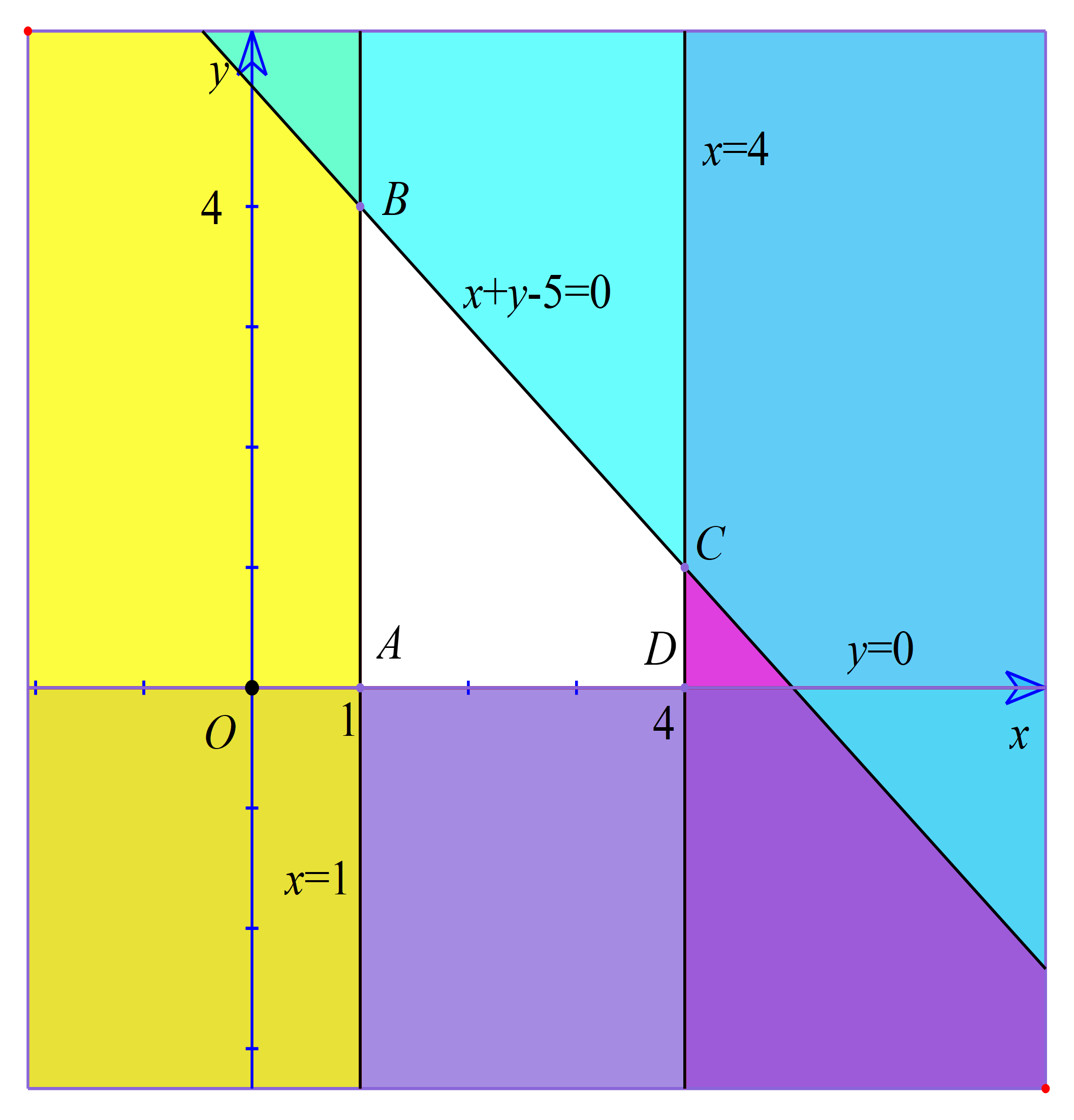
– Miền nghiệm của bất phương trình x ≥ 1 là nửa mặt phẳng kể cả bờ x = 1 và không chứa gốc tọa độ O (như hình 7)
– Miền nghiệm của bất phương trình x ≤ 4 là nửa mặt phẳng kể cả bờ x = 4 và chứa gốc tọa độ O (như hình 7).
– Miền nghiệm của bất phương trình x + y – 5 ≤ 0 là nửa mặt phẳng kể cả bờ x + y – 5 = 0 và chứa gốc tọa độ O (như hình 7).
– Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bên trên trục Ox và kể cả bờ Ox (như hình 7).
Vậy, miền không tô màu (miền tứ giác ABCD, bao gồm cả các cạnh) trong hình 7 là phần giao các miền nghiệm của các bất phương trình trong hệ và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho
 

====== **** mời các bạn xem câu tiếp bên dưới **** =====

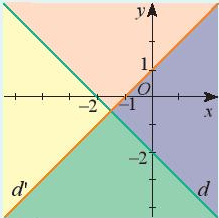
1. Hai đường thẳng d: y = – x – 2 và d’: y = x + 1 chia mặt phẳng tọa độ thành bốn miền khác nhau (không tính hai đường thẳng d và d’) như hình vẽ bên. Để kí hiệu một trong bốn miền đó, người ta đã tạo nhãn: Hãy đặt nhãn này vào miền phù hợp.
   
   

   Câu hỏi:
   

   Hai đường thẳng d: y = – x – 2 và d’: y = x + 1 chia mặt phẳng tọa độ thành bốn miền khác nhau (không tính hai đường thẳng d và d’) như hình vẽ bên. Để kí hiệu một trong bốn miền đó, người ta đã tạo nhãn:
   

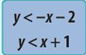
   Hãy đặt nhãn này vào miền phù hợp.
   

   Trả lời:

   Sau bài học này ta sẽ giải bài toán đặt ra bên trên như sau:
   Đường thẳng d trên hình vẽ đi qua hai điểm có tọa độ (-2; 0) và (0; -2). Khi đó phương trình đường thẳng d là y = -x – 2.
   Đường thằng d’ trên hình vẽ đi qua hai điểm có tọa độ (-1; 0) và (0; 1). Khi đó phương trình đường thẳng d’ là: y = x + 1
   Tương ứng với dãn nhãn trên ta có hệ bất phương trình:
   $\left\{\begin{array}{l}y<-x-2\\ y<x+1\end{array}\right.$⟺ $\left\{\begin{array}{l}x+y+2<0\\ -x+y-1<0\end{array}\right.$
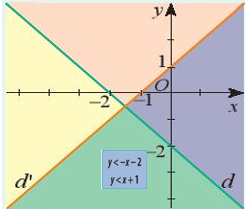
   Ta biểu diễn miền nghiệm của các bất phương trình trong hệ:

   – Miền nghiệm của bất phương trình x + y + 2 < 0 là nửa mặt phẳng có bờ là đường thẳng d: y = -x – 2 (không tính bờ) và không chứa gốc tọa độ O(0; 0).
   – Miền nghiệm của bất phương trình – x + y – 1 < 0 là nửa mặt phẳng có bờ là đường thẳng d’: y = x + 1 (không tính bờ) và chứa gốc tọa độ O(0; 0).
   Vậy miền nghiệm của hệ bất phương trình là giao miền nghiệm của hai bất phương trình trong hệ (miền màu xanh trong hình sau).Vậy vị trí đúng của dán nhãn là:
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng. a) Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y. b) Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên? (20; 40), (40; 20), (-30; 10).
   
   

   Câu hỏi:
   

   Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng.
   a) Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.
   b) Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên?
   (20; 40), (40; 20), (-30; 10).

   Trả lời:

   a) Vì x và y là số sào đất trồng cà tím và cà chua nên x ≥ 0 và y ≥ 0.
   Số tiền để mua hạt giống cho 1 sào đất trồng cà tím là: 200 000 đồng = 0,2 (triệu đồng)
   Số tiền để mua hạt giống cho x sào đất trồng cà tím là: 0,2x (triệu đồng).
   Số tiền để mua hạt giống cho 1 sào đất trồng cà chua là: 100 000 đồng = 0,1 (triệu đồng).
   Số tiền để mua hạt giống cho y sào đất trồng cà chua là: 0,1y (triệu đồng).
   Số tiền để mua cả hai loại hạt giống là: 0,2x + 0,1y (triệu đồng).
   Vì người nông dân có tối đa 9 triệu đồng để mua hạt giống nên ta có bất phương trình: 0,2x + 0,1y ≤ 9.
   Vậy ta có ba bất phương trình mô tả các điều kiện ràng buộc đối với x, y là:
   x ≥ 0.
   y ≥ 0.
   0,2x + 0,1y – 9 ≤ 0.
   b)
   – Với cặp số (20; 40) tương ứng với x = 20, y = 40.
   Ta có: 20 > 0; 40 > 0 và 0,2 . 20 + 0,1 . 40 – 9 = -1 < 0
   Suy ra, cặp số (20; 40) thỏa mãn cả ba bất phương trình trên.
   – Với cặp số (40; 20) tương ứng với x = 40, y = 20.
   Ta có: 40 > 0; 20 > 0 và 0,2 . 40 + 0,1 . 20 – 9 = 1 > 0
   Do đó, cặp số (40; 20) không thỏa mãn bất phương trình 0,2x + 0,1y – 9 ≤ 0.
   Suy ra, cặp số (40; 20) không thỏa mãn đồng thời cả ba bất phương trình trên.
   – Với cặp số (-30; 10) tương ứng với x = -30, y = 10.
   Ta có: -30 < 0; 10 > 0 và 0,2 . (-30) + 0,1 . 10 – 9 = -14 < 0
   Do đó, cặp số (-30; 10) không thỏa mãn bất phương trình x ≥ 0.
   Suy ra, cặp số (-30; 10) không thỏa mãn đồng thời cả ba bất phương trình trên.
   Vậy chỉ có cặp số (20; 40) thỏa mãn cả ba bất phương trình trên.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1.
   
   

   Câu hỏi:
   

   Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1.

   Trả lời:

   a) Hệ bất phương trình $\left\{\begin{array}{c}3x+y-1\le 0\\ 2x-y+2\ge 0\end{array}\right.$
   + Lấy cặp số (0; 0), ta có 3.0 + 0 – 1 = -1 ≤ 0 và 2.0 – 0 + 2 = 2 ≥ 0 là các mệnh đề đúng. Suy ra cặp số (0 ; 0) thỏa mãn cả hai bất phương trình trong hệ bất phương trình.
   Do đó cặp số (0; 0) là một nghiệm của hệ bất phương trình  $\left\{\begin{array}{c}3x+y-1\le 0\\ 2x-y+2\ge 0\end{array}\right.$.
   + Lấy cặp số (0; 1), ta có 3.0 + 1 – 1 = 0 ≤ 0 và 2.0 – 1 + 2 = 1 ≥ 0 là các mệnh đề đúng. Suy ra cặp số (0 ; 1) thỏa mãn cả hai bất phương trình trong hệ bất phương trình.
   Do đó cặp số (0; 1) là một nghiệm của hệ bất phương trình  $\left\{\begin{array}{c}3x+y-1\le 0\\ 2x-y+2\ge 0\end{array}\right.$.
   Vậy hai cặp số (0; 0), (0; 1) là nghiệm của hệ bất phương trình  $\left\{\begin{array}{c}3x+y-1\le 0\\ 2x-y+2\ge 0\end{array}\right.$.
   c) Hệ bất phương trình $\left\{\begin{array}{c}y-1<0\\ x+2\ge 0\end{array}\right.$
   + Lấy cặp số (0; 0), ta có 0 – 1 = -1 < 0 và 0 + 2 ≥ 0 là mệnh đề đúng. Suy ra cặp số (0; 0) thỏa mãn các bất phương trình của hệ bất phương trình.
   Do đó, cặp số (0; 0) là một nghiệm của hệ bất phương trình  $\left\{\begin{array}{c}y-1<0\\ x+2\ge 0\end{array}\right.$
   + Lấy cặp số (1; 0), ta có 0 – 1 = -1 < 0 và 1 + 2 ≥ 0 là các mệnh đề đúng. Suy ra cặp số (1; 0) thỏa mãn các bất phương trình trong hệ bất phương trình.
   Do đó, cặp số (1; 0) là một nghiệm của hệ bất phương trình  $\left\{\begin{array}{c}y-1<0\\ x+2\ge 0\end{array}\right.$.
   Vậy hai cặp số (0; 0) và (1; 0) là nghiệm của hệ bất phương trình $\left\{\begin{array}{c}y-1<0\\ x+2\ge 0\end{array}\right.$

   d) Hệ bất phương trình $\left\{\begin{array}{c}x+y-3\le 0\\ -2x+y+3\ge 0\\ x\ge 0\\ y\ge 0\end{array}\right.$
   + Lấy cặp số (0; 0), thỏa mãn $\left\{\begin{array}{c}0+0-3=-3\le 0\\ -2.0+0+3=3\ge 0\\ 0\ge 0\\ 0\ge 0\end{array}\right.$
   Do đó cặp số (0; 0) là một nghiệm của hệ bất phương trình bất phương trình đã cho.
   + Lấy cặp số (1; 1), thỏa mãn $\left\{\begin{array}{c}1+1-3=-1\le 0\\ -2.1+1+3=2\ge 0\\ 1\ge 0\\ 1\ge 0\end{array}\right.$
   Do đó, cặp số (1; 1) là một nghiệm của hệ bất phương trình  $\left\{\begin{array}{c}x+y-3\le 0\\ -2x+y+3\ge 0\\ x\ge 0\\ y\ge 0\end{array}\right.$
   Vậy hai cặp số (0; 0) và (1; 1) là các nghiệm của hệ bất phương trình  $\left\{\begin{array}{c}x+y-3\le 0\\ -2x+y+3\ge 0\\ x\ge 0\\ y\ge 0\end{array}\right.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hệ bất phương trình x+y−3≤0−2x+y+3≥0. Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho ?
   
   

   Câu hỏi:
   

   Cho hệ bất phương trình $\left\{\begin{array}{c}x+y-3\le 0\\ -2x+y+3\ge 0\end{array}\right.$.
   

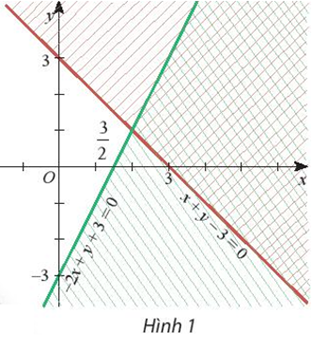
   Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho ?

   Trả lời:

   + Xét miền nghiệm của bất phương trình x + y – 3 ≤ 0 :
   Lấy điểm O(0 ; 0) không thuộc đường thẳng màu đỏ : x + y – 3 = 0, ta có : 0 + 0 – 3 = -3 < 0 nên miền nghiệm của bất phương trình x + y – 3 ≤ 0 là nửa mặt phẳng kể cả bờ là đường thẳng x + y – 3 = 0 và chứa gốc tọa tộ O (là phần không gạch chéo đỏ trong hình 1).
   + Xét miền nghiệm của bất phương trình -2x + y + 3 ≥ 0:
   Lấy điểm O(0 ; 0) không thuộc đường thẳng màu xanh: -2x + y + 3 = 0, ta có : -2.0 + 0 + 3 = 3 > 0 nên miền nghiệm của bất phương trình -2x + y + 3 ≥ 0 là nửa mặt phẳng kể cả bờ là đường thẳng -2x + y + 3 = 0 và chứa gốc tọa độ O (là phần không gạch chéo xanh trong hình 1).
   Vậy miền không gạch chéo (kể cả bờ) trong Hình 1 là miền biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ $\left\{\begin{array}{c}x+y-3\le 0\\ -2x+y+3\ge 0\end{array}\right.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Biểu diễn miền nghiệm của hệ bất phương trình :x+y≤82x+3y≤18x≥0y≥0.
   
   

   Câu hỏi:
   

   Biểu diễn miền nghiệm của hệ bất phương trình :$\left\{\begin{array}{c}x+y\le 8\\ 2x+3y\le 18\\ x\ge 0\\ y\ge 0.\end{array}\right.$

   Trả lời:

   Biểu diễn miền nghiệm của từng bất phương trình trên mặt phẳng Oxy.
   – Xác định miền nghiệm D₁ của bất phương trình x + y ≤ 8:
   Lấy điểm O(0; 0) không thuộc đường thẳng d₁: x + y = 8, ta có: 0 + 0 = 0 < 8. Do đó miền nghiệm của bất phương trình x + y ≤ 8 là nửa mặt phẳng bờ là đường thẳng d (kể cả đường thẳng d₁) và chứa gốc tọa độ O (như hình 3).
   – Xác định miền nghiệm D₂ của bất phương trình 2x +3y ≤ 18:
   Lấy điểm O(0; 0) không thuộc đường thẳng d₂: 2x + 3y = 18, ta có: 2.0 + 3.0 = 0 < 18. Do đó miền nghiệm của bất phương trình 2x +3y ≤ 18 là nửa mặt phẳng bờ là đường thẳng d₂ (kể cả đường thẳng d₂) và chứa gốc tọa độ O (như hình 3).
   – Xác định miền nghiệm D₃ của bất phương trình x ≥ 0:
   Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bên phải trục Oy và kể cả bờ Oy (như hình 3).
   – Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bên trên trục Ox và kể cả bờ Ox (như hình 3).
   
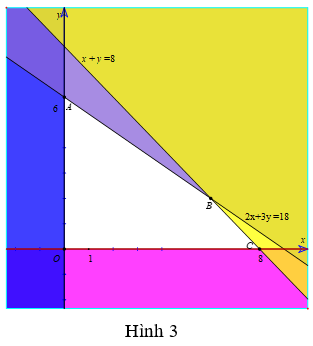
   Vậy, miền không tô màu (miền tứ giác OABC, bao gồm cả các cạnh) trong hình 3 là phần giao của các miền nghiệm của các bất phương trình trong hệ và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====