Cho tứ diện SABC. Gọi G, I lần lượt là trọng tâm của tam giác ABC và SAB. Tìm giao tuyến của mặt phẳng (AIG) và mặt phẳng (SAC)

Câu hỏi:

Cho tứ diện SABC. Gọi G, I lần lượt là trọng tâm của tam giác ABC và SAB. Tìm giao tuyến của mặt phẳng (AIG) và mặt phẳng (SAC)

Trả lời:

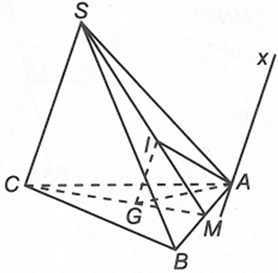
Gọi M là trung điểm của AB.
Do I là trọng tâm của tam giác SAB suy ra $\frac{MI}{MS}=\frac{1}{3}$
Tương tự ta có $\frac{MG}{MC}=\frac{1}{3}$
Suy ra $\frac{MI}{MS}=\frac{MG}{MB}\Rightarrow GI/\text{}/SC$
Từ đó ta có $\left(SAC\right)\cap \left(AIG\right)=Ax$, trong đó Ax // SC // GI

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

   Trả lời:

   

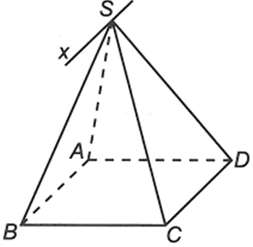
   Ta có $\left\{\begin{array}{l}\left(SAB\right)\cap \left(SCD\right)=S\\ AB\subset \left(SAB\right),CD\subset \left(SCD\right)\\ AB/\text{}/CD\end{array}\right.$
   Suy ra $\left(SAB\right)\cap \left(SCD\right)=Sx$ với $Sx/\text{}/AB/\text{}/CD$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. Tìm giao tuyến của các mặt phẳng: a) SAB∩SCD
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. Tìm giao tuyến của các mặt phẳng:
   a) $\left(SAB\right)\cap \left(SCD\right)$

   Trả lời:

   

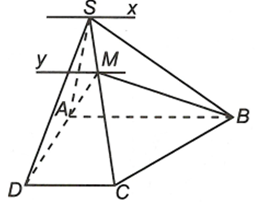
   a) Ta có $\left(SAB\right)\cap \left(SCD\right)=S$, mà AB // CD
   Suy ra $\left(SAB\right)\cap \left(SCD\right)=Sx$, trong đó $Sx/\text{}/AB/\text{}/CD$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) SCD∩MAB
   
   

   Câu hỏi:
   

   b) $\left(SCD\right)\cap \left(MAB\right)$

   Trả lời:

   b) Do $M\in SC$ nên $\left(SCD\right)\cap \left(MAB\right)=M$, mặt khác AB // CD
   $\Rightarrow \left(SCD\right)\cap \left(MAB\right)=My$, trong đó My // AB // CD

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAC) và (SBD)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
   a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAC) và (SBD)

   Trả lời:

   

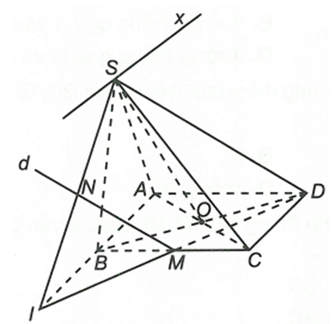
   a) Ta có $\left\{\begin{array}{l}S\in \left(SAB\right)\cap \left(SCD\right)\\ AB\subset \left(SAB\right);CD\subset \left(SCD\right)\\ AB/\text{}/CD\end{array}\right.$
   $\Rightarrow \left(SAB\right)\cap \left(SCD\right)=Sx$ trong đó Sx // AB // CD
   Trong (ABCD) gọi $\left\{O\right\}=AC\cap BD$, suy ra $O\in \left(SAC\right)\cap \left(SBD\right) \left(1\right)$
   Lại có $S\in \left(SAC\right)\cap \left(SBD\right) \left(2\right)$
   Từ (1) và (2), suy ra $SO=\left(SAC\right)\cap \left(SBD\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) Gọi M là trung điểm BC, đường thẳng d qua M và song song SD. Tìm giao điểm của d và mặt phẳng (SAB)
   
   

   Câu hỏi:
   

   b) Gọi M là trung điểm BC, đường thẳng d qua M và song song SD.
   Tìm giao điểm của d và mặt phẳng (SAB)

   Trả lời:

   b) Vì d qua M và song song SD nên $d\subset \left(SDM\right)$
   Lại có $S\in \left(SDM\right)\cap \left(SAB\right)$
   Trong (ABCD) có $\left\{I\right\}=AB\cap DM$suy ra $I\in \left(SDM\right)\cap \left(SAB\right)$
   Khi đó $\left(SDM\right)\cap \left(SAB\right)=SI$
   Trong (SDM) có $\left\{N\right\}=SI\cap d$ suy ra $N=d\cap \left(SAB\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====