Cho hình chóp S.ABCD. Gọi I, J lần lượt là trung điểm của AB và BC. Giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng song song với

Câu hỏi:

Cho hình chóp S.ABCD. Gọi I, J lần lượt là trung điểm của AB và BC. Giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng song song với

A. đường thẳng AD

Đáp án chính xác

B. đường thẳng AB

C. đường thẳng AC

D. đường thẳng BD

Trả lời:

Đáp án A

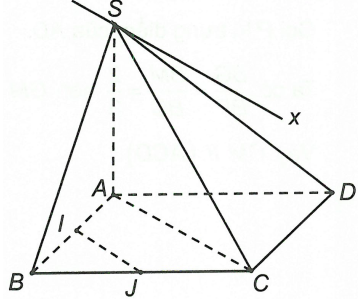
Xét hai mặt phẳng (SAC) và (SIJ) ta có S là điểm chung IJ // AC (đường trung bình trong tam giác).
Suy ta giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng qua S song song với AC

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tứ diện ABCD. Gọi M, N là trung điểm của AB, BC và P là điểm nằm trên cạnh CD. Gọi Q là giao điểm của DA với mặt phẳng (MNP). Chứng minh PQ // MN và PQ // AC
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD. Gọi M, N là trung điểm của AB, BC và P là điểm nằm trên cạnh CD. Gọi Q là giao điểm của DA với mặt phẳng (MNP). Chứng minh PQ // MN và PQ // AC

   Trả lời:

   

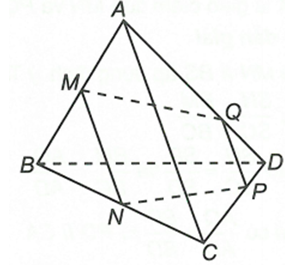
   Ta có $CD\cap \left(MNP\right)=\left\{P\right\}$ và MN // AC
   Suy ra $\left(MNP\right)\cap \left(ACD\right)=Px$
   Trong đó Px // MN // AC
   Mặt khác $DA\cap \left(MNP\right)=\left\{Q\right\}$ nên $Q\in Px$
   Vậy PQ // MN // AC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình chóp S.ABCD đáy ABCD là hình thang với cạnh đáy AB và CD AB>CD. Gọi M, N lần lượt là trung điểm của SA, SB. a) Chứng minh MN // CD
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD đáy ABCD là hình thang với cạnh đáy AB và CD $\left(AB>CD\right)$. Gọi M, N lần lượt là trung điểm của SA, SB.
   a) Chứng minh MN // CD

   Trả lời:

   

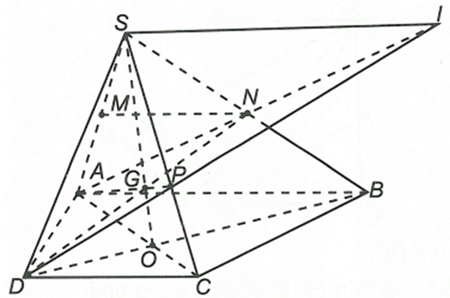
   a) Ta có MN là đường trung bình của tam giác SAB suy ra MN // AB. Mà AB // CD nên MN // CD

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) Tìm giao điểm P của SC và mặt phẳng (AND). Kéo dài AN và DP cắt nhau tại I. Chứng minh SI // AB // CD
   
   

   Câu hỏi:
   

   b) Tìm giao điểm P của SC và mặt phẳng (AND). Kéo dài AN và DP cắt nhau tại I.
   Chứng minh SI // AB // CD

   Trả lời:

   b) Gọi $\left\{O\right\}=AC\cap BD,\left\{G\right\}=SO\cap DN$ và $\left\{P\right\}=AG\cap SC$
   suy ra $\left\{P\right\}=SC\cap \left(ADN\right)$
   Ta có AB // CD nên $\left(SAB\right)\cap \left(SCD\right)=Sx$ sao cho Sx // AB // CD
   Theo đầu bài $\left\{I\right\}=AN\cap DP$ nên $I\in \left(SAB\right)$và $I\in \left(SCD\right)\Rightarrow I\in Sx$
   Từ đó ta có SI // AB // CD

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi M, N, P, Q là các điểm lần lượt trên BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD a) Chứng minh PQ // SA
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi M, N, P, Q là các điểm lần lượt trên BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD
   a) Chứng minh PQ // SA

   Trả lời:

   

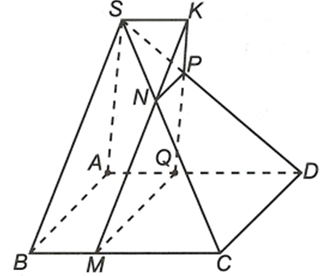
   a) Ta có MN // BS áp dụng định lý Ta-lét ta được $\frac{SN}{SC}=\frac{BM}{BC}$
   Tương tự $\frac{SN}{SC}=\frac{SP}{SD}$và $\frac{BM}{BC}=\frac{AQ}{AD}$
   Từ đó ta có $\frac{AQ}{AD}=\frac{SP}{SD}\Rightarrow PQ/\text{}/SA$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) Gọi K là giao điểm của MN và PQ. Chứng minh SK // SD // BC
   
   

   Câu hỏi:
   

   b) Gọi K là giao điểm của MN và PQ. Chứng minh SK // SD // BC

   Trả lời:

   b) Do AD // BC nên $\left(SAD\right)\cap \left(SBC\right)=Sx$ trong đó Sx // AD // BC
   Mặt khác $\left\{K\right\}=MN\cap QP$ nên K là điểm chung của hai mặt phẳng (SAD) và (SBC) suy ra $K\in Sx$
   Vậy Sx // AD // BC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====