Cho tứ diện ABCD, điểm G là trọng tâm tam giác BCD. Mặt phẳng α qua G, song song với AB và CD. α cắt trung tuyến AM của tam giác ACD tại K. Chọn khẳng định đúng.

Câu hỏi:

Cho tứ diện ABCD, điểm G là trọng tâm tam giác BCD. Mặt phẳng $\left(\alpha \right)$ qua G, song song với AB và CD. $\left(\alpha \right)$ cắt trung tuyến AM của tam giác ACD tại K. Chọn khẳng định đúng.

A. $\left(\alpha \right)$ cắt tứ diện ABCD theo thiết diện là một hình tam giác

B. $AK=\frac{2}{3}AM.$

Đáp án chính xác

C. $AK=\frac{1}{3}AM.$

D. Giao tuyến của $\left(\alpha \right)$ và $\left(CBD\right)$ cắt CD

Trả lời:

Đáp án B

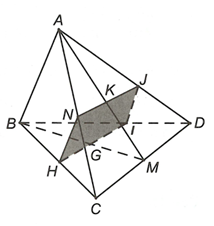
$\left(\alpha \right)$ qua G, song song với CD $\Rightarrow \left(\alpha \right)\cap \left(BCD\right)=HI$ (giao tuyến đi qua G và song song CD, $H\in BC,I\in CD$).
Tương tự ta được $\left(\alpha \right)\cap \left(ABD\right)=IJ$ sao cho $IJ\text{ // }AB.$
$\left(\alpha \right)\cap \left(ACD\right)=JN$sao cho $JN\text{ // }CD.$
$\left(\alpha \right)\cap \left(ABC\right)=HN.$

Vậy $\left(\alpha \right)$ là $\left(HNJI\right)$
Vì G là trọng tâm tam giác BCD mà $IG\text{ // }CD$nên $\frac{BG}{BM}=\frac{BI}{BC}=\frac{2}{3}.$
Mặt khác IJ song song AB nên $\frac{BI}{BC}=\frac{AJ}{AD}=\frac{2}{3}.$
Lại có JK song song DM (vì $K\in AM,M\in CD$) nên $\frac{AK}{AM}=\frac{AJ}{AD}=\frac{2}{3}.$
Vậy $AK=\frac{2}{3}AM.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là tâm hình bình hành ABCD. M là trung điểm của SB. Tìm thiết diện của mặt phẳng α với hình chóp S.ABCD nếu α đi qua M; song song với SD và CD.
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là tâm hình bình hành ABCD. M là trung điểm của SB. Tìm thiết diện của mặt phẳng $\left(\alpha \right)$ với hình chóp S.ABCD nếu $\left(\alpha \right)$ đi qua M; song song với SD và CD.

   Trả lời:

   

   Ta có $M\in \left(\alpha \right)$ và $M\in \left(SAB\right).$
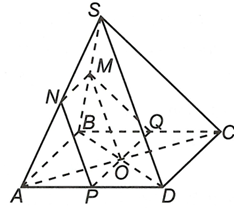
   Mặt khác $CD\text{ // }\left(\alpha \right)$ suy ra $\left(\alpha \right)\cap \left(SAB\right)=Mx$ trong đó $Mx\text{ // }CD$ và $Mx\cap SA=\left\{N\right\}.$
   Ta lại có MO là đường trung bình của tam giác SBD nên $\text{MO // }SD\Rightarrow O\in \left(\alpha \right).$
   Suy ra $\left(\alpha \right)\cap \left(ABCD\right)=Oy,\text{ Oy // }CD$ và Oy cắt AD và BC lần lượt tại P, Q.
   Vậy MNPQ là thiết diện của mặt phẳng $\left(\alpha \right)$ với hình chóp S.ABCD.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tứ diện ABCD. Trên các cạnh BC, CD, AD lấy các điểm M, N, P lần lượt là trung điểm của chúng. Dựng thiết diện của ABCD với mặt phẳng  
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD. Trên các cạnh BC, CD, AD lấy các điểm M, N, P lần lượt là trung điểm của chúng. Dựng thiết diện của ABCD với mặt phẳng  

   Trả lời:

   
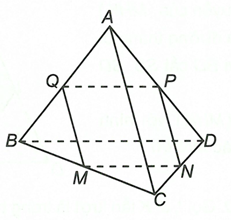
   Ta có MN là đường trung bình của tam giác BCD nên MN // BD

   Do $P\in AD$ nên $\left(MNP\right)\cap \left(ABD\right)=Px$ sao cho $Px\text{ // }BD$ và $Px\cap AB=\left\{Q\right\}.$
   Khi đó thiết diện của mặt phẳng (MNP) với tứ diện ABCD là tứ giác MNPQ.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình chóp S.ABCD có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N lần lượt là trung điểm của các cạnh SB và SC.a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N lần lượt là trung điểm của các cạnh SB và SC.
   a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)

   Trả lời:

   

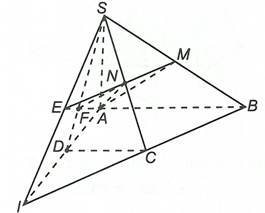
   a) Ta có S là điểm chung thứ nhất của hai mặt phẳng (SAD) và (SBC)
   Kéo dài BC cắt AD tại I. Khi đó I là điểm chung thứ hai của hai mặt phẳng (SAD) và (SBC)
   Suy ra SI là giao tuyến của hai mặt phẳng (SAD) và (SBC)
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
   
   

   Câu hỏi:
   

   b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)

   Trả lời:

   b) Trong mặt phẳng (SBC) kéo dài MN cắt SI tại E.
   Gọi F là giao điểm của AE và SD
   Ta có $F\in SD$ và $F\in AE$mà $AE\subset \left(AMN\right)$nên $\left\{F\right\}=SD\cap \left(AMN\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. c) Dựng thiết diện của hình chóp với mặt phẳng (AMN)
   
   

   Câu hỏi:
   

   c) Dựng thiết diện của hình chóp với mặt phẳng (AMN)

   Trả lời:

   c) Ta có $MN\text{ // }BC$ nên $BC\text{ // }\left(AMN\right)$
   Thiết diện (AMN) với hình chóp S.ABCD là tứ giác AMNF.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====