Hàm số y = x2 + 2x – 1 có bảng biến thiên là

Câu hỏi:

Hàm số y = x² + 2x – 1 có bảng biến thiên là

A.

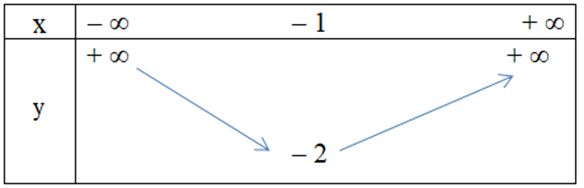
Đáp án chính xác

B.

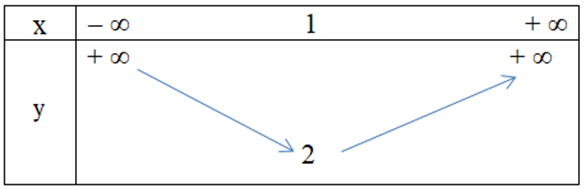
C.

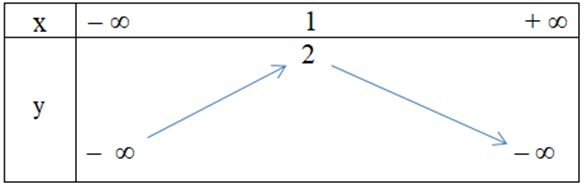
D.

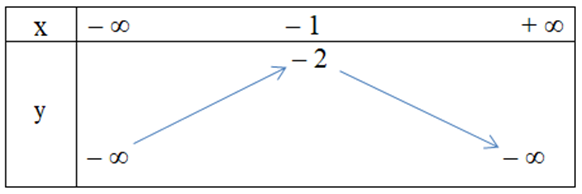
Trả lời:

Đáp án đúng là: A
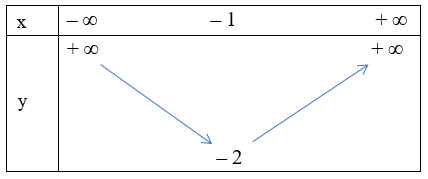
Tọa độ đỉnh của hàm số là I(– 1; – 2)
Vì hệ số a > 0 nên hàm số đồng biến trên khoảng (– 1; + ∞) và nghịch biến trên khoảng (– ∞; – 1) ta có bảng biến thiên

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trục đối xứng của parabol y = x2 – 4x + 1
   
   

   Câu hỏi:
   

   Trục đối xứng của parabol y = x² – 4x + 1

   A. x = 2;

   Đáp án chính xác

   B. x = – 2;

   C. x = 4;

   D. x = – 4.

   Trả lời:

   Đáp án đúng là: A
   Trục đối xứng \({\rm{x}}\,{\rm{ = }}\,–\frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{ = }}–\frac{{–\,{\rm{4}}}}{{\rm{2}}}{\rm{ = }}\,{\rm{2}}\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tọa độ đỉnh I của hàm số y = – 3×2 + 4x – 1
   
   

   Câu hỏi:
   

   Tọa độ đỉnh I của hàm số y = – 3x² + 4x – 1

   A. \({\rm{I}}\left( {–\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\);

   B. \({\rm{I}}\left( {\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\);

   Đáp án chính xác

   C. \({\rm{I}}\left( {\frac{{\rm{4}}}{{\rm{3}}}{\rm{;}}–{\rm{1}}} \right)\);

   D. \({\rm{I}}\left( {\frac{2}{{\rm{3}}}{\rm{;}}\frac{4}{{\rm{3}}}} \right)\).

   Trả lời:

   Đáp án đúng là: B
   Tọa độ đỉnh \({\rm{I}}\left( {–\frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{;}}–\frac{{\rm{\Delta }}}{{{\rm{4a}}}}} \right)\)
   Ta có giá trị \( – \frac{b}{{2a}} = – \frac{4}{{2.( – 3)}} = \frac{2}{3}\),
   giá trị \( – \frac{\Delta }{{4a}} = – \frac{{{4^2} – 4.( – 3).( – 1)}}{{4.( – 3)}} = \frac{1}{3}\).
   Vậy toạ độ đỉnh I\(\left( {\frac{2}{3};\frac{1}{3}} \right)\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số y = 2×2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
   
   

   Câu hỏi:
   

   Cho hàm số y = 2x² – 4x – 1. Kết luận nào đúng trong các kết luận sau

   A. Hàm số đồng biến trên khoảng (0; + ∞);

   B. Hàm số đồng biến trên khoảng (– ∞; 1);

   C. Hàm số nghịch biến trên khoảng (– ∞; 0);

   Đáp án chính xác

   D. Hàm số nghịch biến trên khoảng (– ∞; 2).

   Trả lời:

   Đáp án đúng là: C
   Tọa độ đỉnh của hàm số là I(1; – 3)
   Bảng biến thiên
   

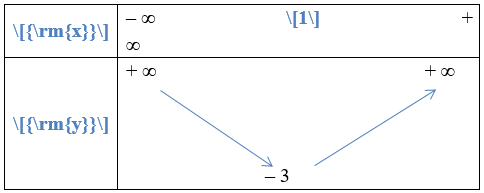
   Từ bảng biến thiên ta có hàm số nghịch biến trên khoảng (– ∞; 1) nên cũng nghịch biến trên khoảng (– ∞; 0).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh I(– 1; – 5)
   
   

   Câu hỏi:
   

   Cho parabol y = ax² + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
   I(– 1; – 5)

   A. a = 1; b = 2;

   B. a = 1; b = – 2;

   C. a = – 2; b = 4;

   D. a = 2; b = 4.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Tọa độ đỉnh của parabol là \({\rm{I}}\left( { – \frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{;}} – \frac{{\rm{\Delta }}}{{{\rm{4a}}}}} \right)\)
   Ta có
    \(\left\{ \begin{array}{l}–\frac{b}{{2a}} = – 1\\ – \frac{{{b^2} – 4ac}}{{4a}} = – 5\\a \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\4{a^2} – 8a = 0\\{\rm{a}} \ne {\rm{0}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 2a\\\left[ \begin{array}{l}a = 0\\a = 2\end{array} \right.\\{\rm{a}} \ne {\rm{0}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\end{array} \right.\)
   Vậy a = 2 và b = 4.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
   
   

   Câu hỏi:
   

   Hàm số y = – x² + 2x + 1 đồng biến trên khoảng

   A. (– ∞; + ∞);

   B. (– ∞; 1);

   Đáp án chính xác

   C. (1; + ∞);

   D. (– ∞; 2).

   Trả lời:

   Đáp án đúng là: B
   Tọa độ đỉnh của hàm số là I(1; 2)
   Bảng biến thiên
   

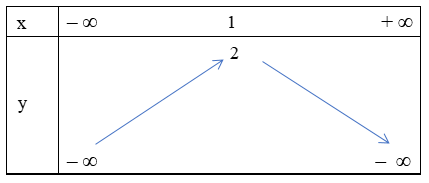
   Từ bảng biến thiên ta có hàm số tăng từ trái sang phải trên khoảng (– ∞; 1) nên hàm số đồng biến trên khoảng (– ∞; 1).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====