Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = 2×2 + 4x + 3 có trục đối xứng là đường thẳng nào?

Câu hỏi:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = 2x² + 4x + 3 có trục đối xứng là đường thẳng nào?

A. x = 2;

B. x = 1;

C. x = -1;

Đáp án chính xác

D. x = 0.

Trả lời:

Hướng dẫn giải
Đáp án đúng là: C
Hàm số bậc hai y = 2x² + 4x + 3 xác định các tham số: a = 2; b = 4; c = 3.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax² + bx + c có trục đối xứng là đường thẳng x = $-\frac{b}{2\text{a}}$.
Vậy đồ thị bậc hai y = 2x² + 4x + 3 có trục đối xứng là đường thẳng x = – 1.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các hàm số sau, hàm số nào là hàm số bậc hai?
   
   

   Câu hỏi:
   

   Trong các hàm số sau, hàm số nào là hàm số bậc hai?

   A. y = 2x + 1;

   B. y = x² + 2x – 1;

   Đáp án chính xác

   C. y = x³ – 1;

   D. y = 1

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Hàm số bậc hai ẩn x là hàm số cho bởi công thức có dạng y = f(x) = ax² + bx + c với a, b, c là các số thực và a khác 0. Ta thấy chỉ có câu B là hàm số có dạng y = f(x) = ax² + bx + c với a = 1 ≠ 0; b = 2, c = – 1.
   Vậy ta chọn phương án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Điền vào chỗ trống: Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) là một ….
   
   

   Câu hỏi:
   

   Điền vào chỗ trống: Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax² + bx + c (với a ≠ 0) là một ….

   A. Parabol;

   Đáp án chính xác

   B. Đường thẳng;

   C. Tia;

   D. Hyperbol.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: A
   Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax² + bx + c (với a ≠ 0) là một Parabol.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Bề lõm của parabol quay lên trên đối với đồ thị hàm số bậc hai nào sau đây?
   
   

   Câu hỏi:
   

   Bề lõm của parabol quay lên trên đối với đồ thị hàm số bậc hai nào sau đây?

   A. y = -x²;

   B. y = 2 + 2x – 3x²;

   C. y = 2x + x²;

   Đáp án chính xác

   D. y = x – x².

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   Bề lõm của parabol quay lên trên khi hàm số bậc hai có giá trị a > 0.
   Trong các đáp án A, B, C, D ta thấy chỉ có câu C là a = 1 > 0, các câu A, B, D đều có hệ số a < 0 nên câu C đúng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Một chiếc cổng hình parabol có dạng đồ thị giống đồ thị hàm số y =- 12×2  như hình vẽ. Cổng có chiều rộng d = 8 m. Tính chiều cao h của cổng.
   
   

   Câu hỏi:
   

   Một chiếc cổng hình parabol có dạng đồ thị giống đồ thị hàm số y =- $\frac{1}{2}$x²  như hình vẽ. Cổng có chiều rộng d = 8 m. Tính chiều cao h của cổng.
   

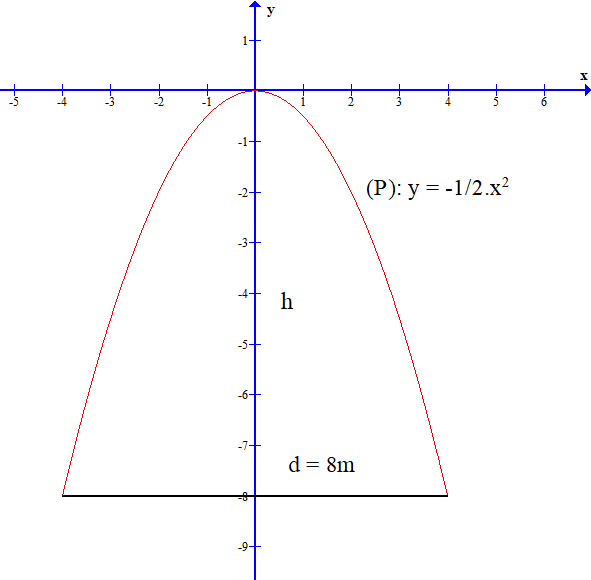
   A. h = 4m

   B. h = 8m

   Đáp án chính xác

   C. h = 10m

   D. h = 16m

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Gọi A là 1 điểm nằm ở bên phải chân cổng.
   Hoành độ điểm A là bằng một nửa chiều rộng của cổng.
   Tung độ của điểm A bằng chiều cao của cổng.
   
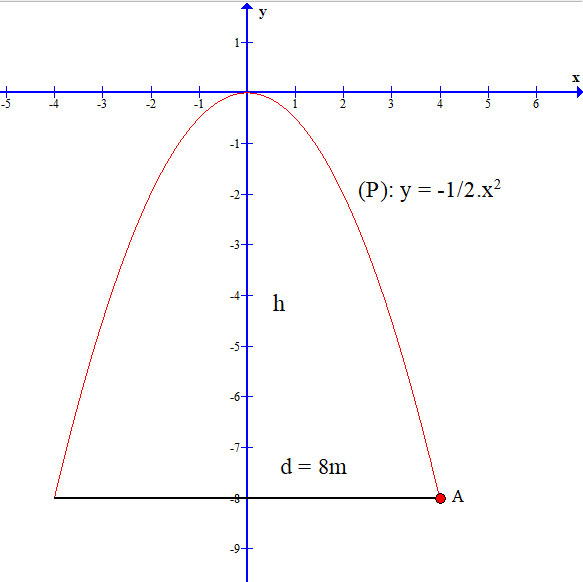
   Parabol (P): y = $–\frac{1}{2}$x² có d = 8 m, suy ra $x_A=\frac{d}{2}=4$.
   A thuộc (P) suy ra y_A = $–\frac{1}{2}$. 4² = ‒8.
   Vậy chiều cao của cổng là h = 8 m.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm tọa độ đỉnh S của parabol: y = x2 – 2x + 1?
   
   

   Câu hỏi:
   

   Tìm tọa độ đỉnh S của parabol: y = x² – 2x + 1?

   A. S(0; 0);

   B. S(1; 0);

   Đáp án chính xác

   C. S(0; 1);

   D. S(1; 1).

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax² + bx + c (với a ≠ 0) là một parabol (P): Có đỉnh S với hoành độ $x_S=-\frac{b}{2a}$, tung độ $y_S=-\frac{\Delta }{4a}$; (Δ = b² – 4ac)
   Với hàm số y = x² – 2x + 1 có a = 1, b = – 2, c = 1 thì đỉnh S có toạ độ là:
   $x_S=-\frac{b}{2a}$= 1, $y_S=-\frac{\Delta }{4a}$= 0.
   Vậy S(1; 0).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====