Câu hỏi:
An vẽ biểu đồ thể hiện tỉ lệ số lượng mỗi loại cây ăn quả trong một nông trại theo bảng thống kê dưới đây:
Loại cây ăn quả
Cây cam
Cây xoài
Cây mận
Cây táo
Cây chanh
Số cây
50
30
25
30
20
Biểu đồ An vẽ như sau:
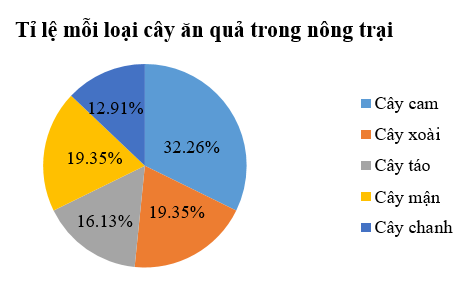
Hãy cho biết biểu đồ An vẽ chính xác chưa? Nếu chưa thì cần điều chỉnh như thế nào cho đúng?
A. Chưa chính xác, cần đổi chỗ “Cây táo” và “Cây mận” ở phần chú thích;
Đáp án chính xác
B. Chưa chính xác, cần đổi chỗ “Cây xoài” và “Cây táo” ở phần chú thích
C. Chưa chính xác, cần đổi chỗ “Cây chanh” và “Cây mận” ở phần chú thích;
D. Biểu đồ An vẽ đã chính xác.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Theo bảng thống kê thì số lượng cây táo nhiều hơn số lượng cây mận và số cây táo bằng số cây xoài.
Nên trên biểu đồ hình quạt, hình quạt biểu diễn tỉ lệ cây táo phải nhiều hơn tỉ lệ cây mận và tỉ lệ cây táo bằng tỉ lệ cây xoài.
Do đó biểu đồ An vẽ chưa chính xác.
Ở phần chú thích, An nên đổi chỗ “Cây táo” và “Cây mận” thì sẽ được biểu đồ chính xác.
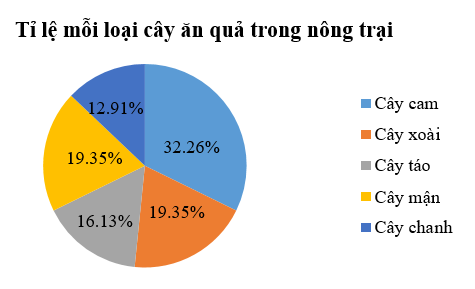
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập xác định của hàm số \(y = \frac{{x – 1}}{{{x^2} – x + 3}}\) là
Câu hỏi:
Tập xác định của hàm số \(y = \frac{{x – 1}}{{{x^2} – x + 3}}\) là
A. \(\emptyset \);
B. ℝ;
Đáp án chính xác
C. ℝ\{1};
D. ℝ\{0; 1}.
Trả lời:
Đáp án đúng là: B
Ta có: \({x^2} – x + 3 = {\left( {x – \frac{1}{2}} \right)^2} + \frac{{11}}{4} > 0{\rm{ }}\forall x \in \mathbb{R}\).
Vậy hàm số có tập xác định D = ℝ.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số có đồ thị như hình vẽ
Kết luận nào sau đây là đúng
Câu hỏi:
Cho hàm số có đồ thị như hình vẽ
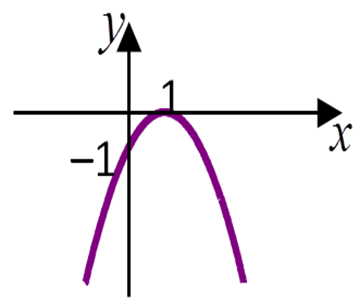
Kết luận nào sau đây là đúng
A. Hàm số nghịch biến trên khoảng (– ∞; – 1);
B. Hàm số đồng biến trên khoảng (1; + ∞);
C. Hàm số đồng biến trên khoảng (– ∞; 1);
Đáp án chính xác
D. Hàm số nghịch biến trên khoảng (– 1; + ∞).
Trả lời:
Đáp án đúng là: C
Quan sát đồ thị hàm số, ta thấy:
Đồ thị ta có hàm số đi lên trên khoảng (– ∞; 1) và đi xuống trên khoảng (1; + ∞) nên hàm số đồng biến trên khoảng (– ∞; 1) và nghịch biến trên khoảng (1; + ∞).
Vậy đáp án đúng là C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
Câu hỏi:
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
A. I(– 4; – 4);
Đáp án chính xác
B. I(– 1; – 1);
C. I(– 4; 4);
D. I(4; 4).
Trả lời:
Đáp án đúng là : A
Tọa độ đỉnh \(I\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right)\)
Ta có \( – \frac{b}{{2a}} = – \frac{8}{{2.1}} = – 4\); \( – \frac{\Delta }{{4a}} = – \frac{{{8^2} – 4.1.12}}{{4.1}} = – 4\)
Vậy tọa độ đỉnh I(– 4; – 4)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị hàm số y = – 9×2 + 6x – 1 có dạng là:
Câu hỏi:
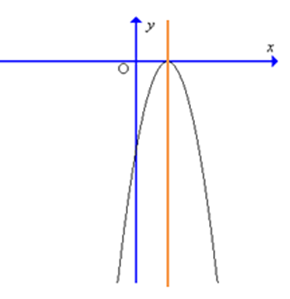
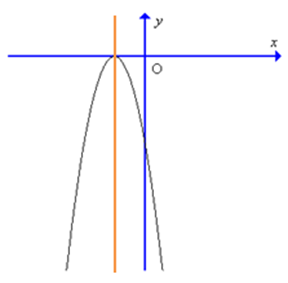
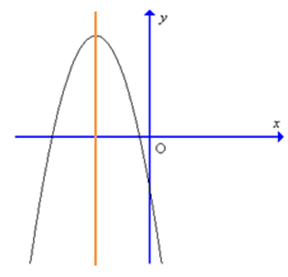
Đồ thị hàm số y = – 9x2 + 6x – 1 có dạng là:
A.
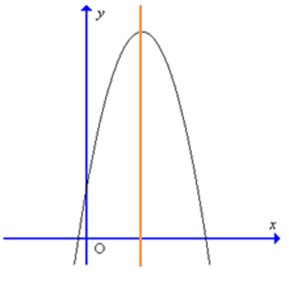
B.
Đáp án chính xác
C.
D.
Trả lời:
Đáp án đúng là: B
Giao điểm của đồ thị hàm số với trục tung là điểm A(0; – 1) vậy giao điểm có tung độ âm nên loại đáp án A.
Trục đối xứng của đồ thị hàm số \(x = – \frac{b}{{2a}} = – \frac{6}{{2.( – 9)}} = \frac{1}{3}\) vậy trục đối xứng nằm về phần dương của trục Ox nên loại đáp án C và D.
Vậy đáp án đúng là B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
Câu hỏi:
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
A. f(x) < 0 khi x ∈ (– 1; 1);
B. f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞)
C. f(x) = 0 khi x = 1; x = – 1;
D. f(x) > 0 khi x ∈ (– 1; 1);
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Xét f(x) = x2 – 1 có ∆ = – 4.(–1) = 4 > 0, a = 1 > 0 và có hai nghiệm phân biệt x1 = –1 và x2 = 1.
Khi đó ta có bảng xét dấu:
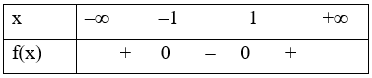
Từ bảng xét dấu ta có f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞); f(x) < 0 khi x ∈ (– 1; 1)
Vậy khẳng định sai là D====== **** mời các bạn xem câu tiếp bên dưới **** =====