Câu hỏi:
Một cảnh sát giao thông bắn tốc độ (đơn vị: km/h) của 13 chiếc xe qua trạm và ghi lại kết quả như sau:
20
40
35
45
70
45
40
25
35
40
45
35
25
Hỏi mật độ số liệu tập trung chủ yếu ở đâu?
A. Bên trái Q2;
B. Bên phải Q2;
Đáp án chính xác
C. Số liệu dàn trải đều;
D. Không thể biết được mật độ số liệu tập trung chủ yếu ở đâu.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Sắp xếp lại mẫu số liệu theo thứ tự không giảm ta được: 20; 25; 25; 35; 35; 35; 40; 40; 40; 45; 45; 45; 70.
– Vì cỡ mẫu n = 13 = 2.6 + 1 là số lẻ, nên giá trị tứ phân vị thứ hai là số liệu thứ 7, tức là Q2 = 40.
– Tứ phân vị thứ nhất là trung vị của mẫu (gồm nửa số liệu bên trái Q2 và không kể Q2): 20; 25; 25; 35; 35; 35.
Do đó Q1 = (25 + 35) : 2 = 30.
– Tứ phân vị thứ ba là trung vị của mẫu (gồm nửa số liệu bên phải Q2 và không kể Q2): 40; 40; 45; 45; 45; 70.
Do đó Q3 = (45 + 45) : 2 = 45.
Ta có Q2 – Q1 = 40 – 30 = 10 và Q3 – Q2 = 45 – 40 = 5.
Vì 10 > 5 nên khoảng cách giữa Q1 và Q2 lớn hơn khoảng cách giữa Q2 và Q3.
Ta suy ra mật độ số liệu ở bên trái Q2 thấp hơn ở bên phải Q2.
Vậy ta chọn đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập xác định của hàm số \(y = \frac{{x – 1}}{{{x^2} – x + 3}}\) là
Câu hỏi:
Tập xác định của hàm số \(y = \frac{{x – 1}}{{{x^2} – x + 3}}\) là
A. \(\emptyset \);
B. ℝ;
Đáp án chính xác
C. ℝ\{1};
D. ℝ\{0; 1}.
Trả lời:
Đáp án đúng là: B
Ta có: \({x^2} – x + 3 = {\left( {x – \frac{1}{2}} \right)^2} + \frac{{11}}{4} > 0{\rm{ }}\forall x \in \mathbb{R}\).
Vậy hàm số có tập xác định D = ℝ.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số có đồ thị như hình vẽ
Kết luận nào sau đây là đúng
Câu hỏi:
Cho hàm số có đồ thị như hình vẽ
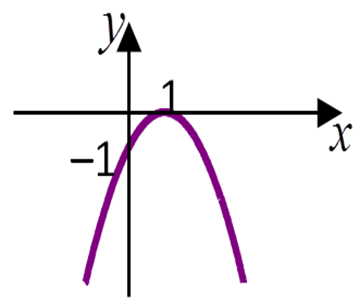
Kết luận nào sau đây là đúng
A. Hàm số nghịch biến trên khoảng (– ∞; – 1);
B. Hàm số đồng biến trên khoảng (1; + ∞);
C. Hàm số đồng biến trên khoảng (– ∞; 1);
Đáp án chính xác
D. Hàm số nghịch biến trên khoảng (– 1; + ∞).
Trả lời:
Đáp án đúng là: C
Quan sát đồ thị hàm số, ta thấy:
Đồ thị ta có hàm số đi lên trên khoảng (– ∞; 1) và đi xuống trên khoảng (1; + ∞) nên hàm số đồng biến trên khoảng (– ∞; 1) và nghịch biến trên khoảng (1; + ∞).
Vậy đáp án đúng là C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
Câu hỏi:
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
A. I(– 4; – 4);
Đáp án chính xác
B. I(– 1; – 1);
C. I(– 4; 4);
D. I(4; 4).
Trả lời:
Đáp án đúng là : A
Tọa độ đỉnh \(I\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right)\)
Ta có \( – \frac{b}{{2a}} = – \frac{8}{{2.1}} = – 4\); \( – \frac{\Delta }{{4a}} = – \frac{{{8^2} – 4.1.12}}{{4.1}} = – 4\)
Vậy tọa độ đỉnh I(– 4; – 4)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị hàm số y = – 9×2 + 6x – 1 có dạng là:
Câu hỏi:
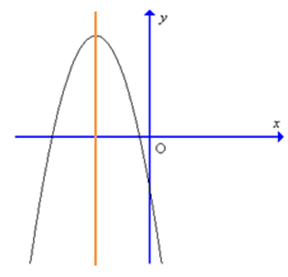
Đồ thị hàm số y = – 9x2 + 6x – 1 có dạng là:
A.
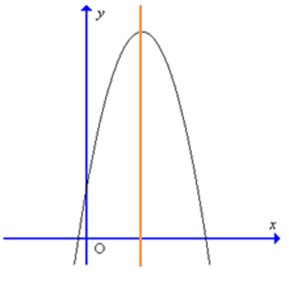
B.
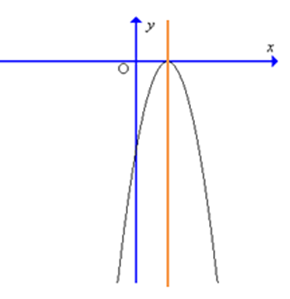
Đáp án chính xác
C.
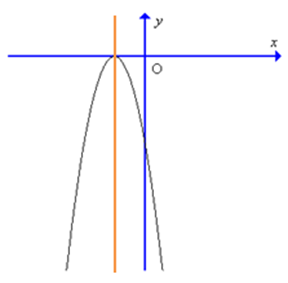
D.
Trả lời:
Đáp án đúng là: B
Giao điểm của đồ thị hàm số với trục tung là điểm A(0; – 1) vậy giao điểm có tung độ âm nên loại đáp án A.
Trục đối xứng của đồ thị hàm số \(x = – \frac{b}{{2a}} = – \frac{6}{{2.( – 9)}} = \frac{1}{3}\) vậy trục đối xứng nằm về phần dương của trục Ox nên loại đáp án C và D.
Vậy đáp án đúng là B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
Câu hỏi:
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
A. f(x) < 0 khi x ∈ (– 1; 1);
B. f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞)
C. f(x) = 0 khi x = 1; x = – 1;
D. f(x) > 0 khi x ∈ (– 1; 1);
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Xét f(x) = x2 – 1 có ∆ = – 4.(–1) = 4 > 0, a = 1 > 0 và có hai nghiệm phân biệt x1 = –1 và x2 = 1.
Khi đó ta có bảng xét dấu:
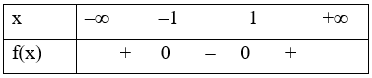
Từ bảng xét dấu ta có f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞); f(x) < 0 khi x ∈ (– 1; 1)
Vậy khẳng định sai là D====== **** mời các bạn xem câu tiếp bên dưới **** =====