Trong mặt phẳng toạ độ Oxy cho ba điểm A(1; 2), B(3; 4) và C(2; –1). Tìm toạ độ tâm I của đường tròn ngoại tiếp và trực tâm H của tam giác ABC.

Câu hỏi:

Trong mặt phẳng toạ độ Oxy cho ba điểm A(1; 2), B(3; 4) và C(2; –1).
Tìm toạ độ tâm I của đường tròn ngoại tiếp và trực tâm H của tam giác ABC.

Trả lời:

Lời giải
* Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Gọi I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Khi đó IA = IB = IC.
Với ba điểm A(1; 2), B(3; 4) và C(2; –1) ta có:
+) \(\overrightarrow {IA} = \left( {1 – a;2 – b} \right)\) \( \Rightarrow \left| {\overrightarrow {IA} } \right| = \sqrt {{{\left( {1 – a} \right)}^2} + {{\left( {2 – b} \right)}^2}} \)
+) \(\overrightarrow {IB} = \left( {3 – a;4 – b} \right)\) \( \Rightarrow \left| {\overrightarrow {IB} } \right| = \sqrt {{{\left( {3 – a} \right)}^2} + {{\left( {4 – b} \right)}^2}} \)
+) \(\overrightarrow {IC} = \left( {2 – a; – 1 – b} \right)\)\( \Rightarrow \left| {\overrightarrow {IC} } \right| = \sqrt {{{\left( {2 – a} \right)}^2} + {{\left( { – 1 – b} \right)}^2}} \)
Do đó IA = IB = IC IA² = IB² = IC²
(1 – a)² + (2 – b)² = (3 – a)² + (4 – b)² = (2 – a)² + (–1 – b)²
\( \Leftrightarrow \left\{ \begin{array}{l}{\left( {1–a} \right)^2} + {\left( {2–b} \right)^2} = {\left( {3–a} \right)^2} + {\left( {4–b} \right)^2}\\{\left( {1–a} \right)^2} + {\left( {2–b} \right)^2} = {\left( {2–a} \right)^2} + {\left( {–1–b} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}1 – 2a + {a^2} + 4 – 4b + {b^2} = 9 – 6a + {a^2} + 16 – 8b + {b^2}\\1 – 2a + {a^2} + 4 – 4b + {b^2} = 4 – 4a + {a^2} + 1 + 2b + {b^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}4a + 4b = 20\\2a – 6b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 5\\a – 3b = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{15}}{4}\\b = \frac{5}{4}\end{array} \right.\)\( \Rightarrow I\left( {\frac{{15}}{4};\frac{5}{4}} \right)\)
* Tìm tọa độ trực tâm H của tam giác ABC.
Gọi H(x₀; y₀) là tọa độ trực tâm của tam giác ABC.
Vì H là trực tâm của tam giác ABC nên theo kết quả của Bài 4.15, phần a) trang 54 ta có \(\overrightarrow {AH} = 2\overrightarrow {IM} \) (với M là trung điểm của BC).
Với A(1; 2), B(3; 4), C(2; –1) và \(I\left( {\frac{{15}}{4};\frac{5}{4}} \right)\)ta có:
• Trung điểm M của BC có tọa độ là: \(\left\{ \begin{array}{ccccc}{x_M} = \frac{{3 + 2}}{2} = \frac{5}{2}\\y{ & _M} = \frac{{4 + \left( { – 1} \right)}}{2} = \frac{3}{2}\end{array} \right.\) \( \Rightarrow M\left( {\frac{5}{2};\frac{3}{2}} \right)\)
• \(\overrightarrow {IM} = \left( {\frac{5}{2} – \frac{{15}}{4};\frac{3}{2} – \frac{5}{4}} \right) = \left( {\frac{{ – 5}}{4};\frac{1}{4}} \right)\)
\( \Rightarrow 2\overrightarrow {IM} = \left( {\frac{{ – 5}}{2};\frac{1}{2}} \right)\)
• \(\overrightarrow {AH} = \left( {{x_0} – 1;{y_0} – 2} \right)\)
Ta có: \(\overrightarrow {AH} = 2\overrightarrow {IM} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_0} – 1 = \frac{{ – 5}}{2}\\{y_0} – 2 = \frac{1}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_0} = \frac{{ – 3}}{2}\\{y_0} = \frac{5}{2}\end{array} \right.\)
\( \Rightarrow H\left( {\frac{{ – 3}}{2};\frac{5}{2}} \right).\)
Vậy \(I\left( {\frac{{15}}{4};\frac{5}{4}} \right)\) và \(H\left( {\frac{{ – 3}}{2};\frac{5}{2}} \right).\)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.

   Trả lời:

   Lời giải
   Cách 1:
   Gọi A(x_A; y_A); B(x_B; y_B) và C(x_C; y_C) là tọa độ ba đỉnh của tam giác ABC.
   Ta có:
   +) M(4; 0) là trung điểm của BC nên \(\left\{ \begin{array}{l}4 = \frac{{{x_B} + {x_C}}}{2}\\0 = \frac{{{y_B} + {y_C}}}{2}\end{array} \right.\)
   \( \Rightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 8\\{y_B} + {y_C} = 0\end{array} \right.\)(1)
   +) N(5; 2) là trung điểm của CA nên \(\left\{ \begin{array}{l}5 = \frac{{{x_A} + {x_C}}}{2}\\2 = \frac{{{y_A} + {y_C}}}{2}\end{array} \right.\)
   \( \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_C} = 10\\{y_A} + {y_C} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 10 – {x_A}\\{y_C} = 4 – {y_A}\end{array} \right.\)(2)
   +) P(2; 3) là trung điểm của AB nên \(\left\{ \begin{array}{l}2 = \frac{{{x_A} + {x_B}}}{2}\\3 = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\)
   \( \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 4\\{y_A} + {y_B} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 4 – {x_A}\\{y_B} = 6 – {y_A}\end{array} \right.\)(3)
   Thay (2) và (3) vào (1) ta được:
   \(\left\{ \begin{array}{l}\left( {4 – {x_A}} \right) + \left( {10 – {x_A}} \right) = 8\\\left( {6 – {y_A}} \right) + \left( {4 – {y_A}} \right) = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}14 – 2{x_A} = 8\\10 – 2{y_A} = 0\end{array} \right.\)
   \( \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{y_A} = 5\end{array} \right.\) A(3; 5)
   Khi đó \(\left\{ \begin{array}{l}{x_B} = 4 – 3 = 1\\{y_B} = 6 – 5 = 1\end{array} \right.\) B(1; 1)
   \(\left\{ \begin{array}{l}{x_C} = 10 – 3 = 7\\{y_C} = 4 – 5 = – 1\end{array} \right.\) C(7; –1)
   Vậy A(3; 5), B(1; 1) và C(7; –1).
   Cách 2:
   
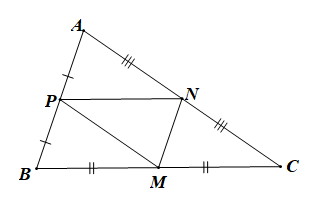
   Do M, N, P
   lần lượt là trung điểm của BC, CA, AB
   Nên MN, NP, PM là các đường trung bình của tam giác ABC.
   MN // AB, NP // BC, MP // AC.
   +) Do MN // BM và NP // BM nên tứ giác MNPB là hình bình hành
   \( \Rightarrow \overrightarrow {MB} = \overrightarrow {NP} \)
   Gọi B(x_B; y_B) và có M(4; 0), N(5; 2) và P(2, 3).
   \( \Rightarrow \overrightarrow {MB} = \left( {{x_B} – 4;{y_B}} \right)\) và \(\overrightarrow {NP} = \left( {2 – 5;3 – 2} \right) = \left( { – 3;1} \right)\)
   Khi đó \(\overrightarrow {MB} = \overrightarrow {NP} \Leftrightarrow \left\{ \begin{array}{l}{x_B} – 4 = – 3\\{y_B} = 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 1\\{y_B} = 1\end{array} \right.\) B(1; 1)
   Tương tự ta cũng có A(3; 5) và C(7; –1).
   Vậy A(3; 5), B(1; 1) và C(7; –1).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong mặt phẳng toạ độ Oxy cho ba điểm A(2;–1), B(1; 4) và C(7; 0). Tính độ dài các đoạn thẳng AB, BC và CA. Từ đó suy ra tam giác ABC là một tam giác vuông cân.
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy cho ba điểm A(2;–1), B(1; 4) và C(7; 0).
   Tính độ dài các đoạn thẳng AB, BC và CA. Từ đó suy ra tam giác ABC là một tam giác vuông cân.

   Trả lời:

   Lời giải
   Với A(2;–1), B(1; 4) và C(7; 0) ta có:
   +) \(\overrightarrow {AB} = \left( {1 – 2;4 – \left( { – 1} \right)} \right) = \left( { – 1;5} \right)\)
   \( \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( { – 1} \right)}^2} + {5^2}} = \sqrt {26} \)
   +) \(\overrightarrow {BC} = \left( {7 – 1;0 – 4} \right) = \left( {6; – 4} \right)\)
   \( \Rightarrow BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{6^2} + {{\left( { – 4} \right)}^2}} = \sqrt {52} = 2\sqrt {13} \)
   +) \(\overrightarrow {CA} = \left( {2 – 7; – 1 – 0} \right) = \left( { – 5; – 1} \right)\)
   \( \Rightarrow CA = \left| {\overrightarrow {CA} } \right| = \sqrt {{{\left( { – 5} \right)}^2} + {{\left( { – 1} \right)}^2}} = \sqrt {26} \)
   Do đó AB = CA \(\left( { = \sqrt {26} } \right)\)
   Nên tam giác ABC cân tại A (1)
   Mặt khác: \(B{C^2} = {\left( {2\sqrt {13} } \right)^2} = 52\)
   Và \(A{B^2} + A{C^2} = {\left( {\sqrt {26} } \right)^2} + {\left( {\sqrt {26} } \right)^2} = 52\)
   BC² = AB² + AC²
   Theo định lí Pythagoras đảo thì tam giác ABC vuông tại A (2)
   Từ (1) và (2) suy ra tam giác ABC vuông cân tại A với \(AB = AC = \sqrt {26} ;BC = 2\sqrt {13} .\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong mặt phẳng toạ độ Oxy cho ba điểm A(2;–1), B(1; 4) và C(7; 0). Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy cho ba điểm A(2;–1), B(1; 4) và C(7; 0).
   Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.

   Trả lời:

   Lời giải
   
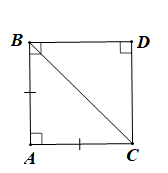
   Vì ABC là tam giác vuông cân
   Nên để ABDC là hình vuông thì tứ giác ABDC là hình bình hành
   \( \Leftrightarrow \overrightarrow {CA} = \overrightarrow {DB} \)
   Gọi D(x_D; y_D) và có A(2;–1), B(1; 4), C(7; 0).
   \( \Rightarrow \overrightarrow {CA} = \left( { – 5; – 1} \right)\)và \(\overrightarrow {DB} = \left( {1 – {x_D};4 – {y_D}} \right)\)
   Do đó \(\overrightarrow {CA} = \overrightarrow {DB} \Leftrightarrow \left\{ \begin{array}{l} – 5 = 1 – {x_D}\\ – 1 = 4 – {y_D}\end{array} \right.\)
   \( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 6\\{y_D} = 5\end{array} \right.\) D(6; 5).
   Vậy tọa độ điểm D cần tìm là D(6; 5).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5). Tìm toạ độ của điểm P thuộc Ox sao cho PM = PN.
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).
   Tìm toạ độ của điểm P thuộc Ox sao cho PM = PN.

   Trả lời:

   Lời giải
   Gọi P(a; 0) là điểm thuộc tia Ox.
   Với M(–2; 1) và N(4; 5) ta có:
   +) \(\overrightarrow {PM} = \left( { – 2 – a;1} \right)\)\( \Rightarrow PM = \left| {\overrightarrow {PM} } \right| = \sqrt {{{\left( { – 2 – a} \right)}^2} + {1^2}} \)
   +) \(\overrightarrow {PN} = \left( {4 – a;5} \right)\)\( \Rightarrow PN = \left| {\overrightarrow {PN} } \right| = \sqrt {{{\left( {4 – a} \right)}^2} + {5^2}} \)
   Do đó PM = PN \( \Leftrightarrow \sqrt {{{\left( { – 2 – a} \right)}^2} + {1^2}} = \sqrt {{{\left( {4 – a} \right)}^2} + {5^2}} \)
   (–2 – a)² + 1² = (4 – a)² + 5²
   4 + 4a + a² + 1 = 16 – 8a + a² + 25
   12a = 36
   a = 3.
   Vậy P(3; 0).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5). Tìm toạ độ của điểm Q sao cho \(\overrightarrow {MQ} = 2\overrightarrow {PN} .\)
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).
   Tìm toạ độ của điểm Q sao cho \(\overrightarrow {MQ} = 2\overrightarrow {PN} .\)

   Trả lời:

   Lời giải
   Giả sử điểm Q có tọa độ là Q(x; y).
   Với M(–2; 1), N(4; 5) và P(3; 0) ta có:
   +) \(\overrightarrow {MQ} = \left( {x + 2;y – 1} \right)\)
   +) \(\overrightarrow {PN} = \left( {4 – 3;5 – 0} \right) = \left( {1;5} \right)\)
   \( \Rightarrow 2\overrightarrow {PN} = \left( {2;10} \right)\)
   Do đó \(\overrightarrow {MQ} = 2\overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l}x + 2 = 2\\y – 1 = 10\end{array} \right.\)
   \( \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 11\end{array} \right.\) Q(0; 11).
   Vậy Q(0; 11).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====