Lý thuyết Toán lớp 10 Bài 3: Dấu của tam thức bậc hai

Với tóm tắt lý thuyết Toán lớp 10 Bài 3: Dấu của tam thức bậc hai sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Bài 3: Dấu của tam thức bậc hai

Video giải Toán 10 Bài 3: Dấu của tam thức bậc hai – Cánh diều
A. Lý thuyết Dấu của tam thức bậc hai
1. Dấu của tam thức bậc hai
Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0), ∆ = b² – 4ac.
+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ
+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ \ $\left\{\frac{-\mathrm{b}}{2\text{a}}\right\}$
+ Nếu ∆ > 0 thì f(x) có hai nghiệm x₁, x₂ (x₁ < x₂). Khi đó:
– f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng (–∞; x₁); (x₂; +∞)
– f(x) trái dấu với hệ số a với mọi x thuộc khoảng (x₁; x₂).
2. Ví dụ
2.1. Ví dụ 1
Xét dấu của tam thức bậc hai
a) f(x) = 4x² – x + 1;
b) f(x) = x² + 2x + 1.
Hướng dẫn giải
a) Tam thức bậc hai f(x) = 4x² – x + 1 có ∆ = b² – 4ac = (– 1)² – 4.4.1 = –15 < 0, hệ số
a = 4 > 0 nên f(x) > 0 với mọi x ∈ ℝ.
b) Tam thức bậc hai f(x) = x² + 2x + 1 có ∆ = b² – 4ac = 2² – 4.1.1 = 0, hệ số a = 1 > 0, nghiệm kép x₀ = – 1 nên f(x) > 0 với mọi x ∈ ℝ \ {– 1}.
2.2. Ví dụ 2
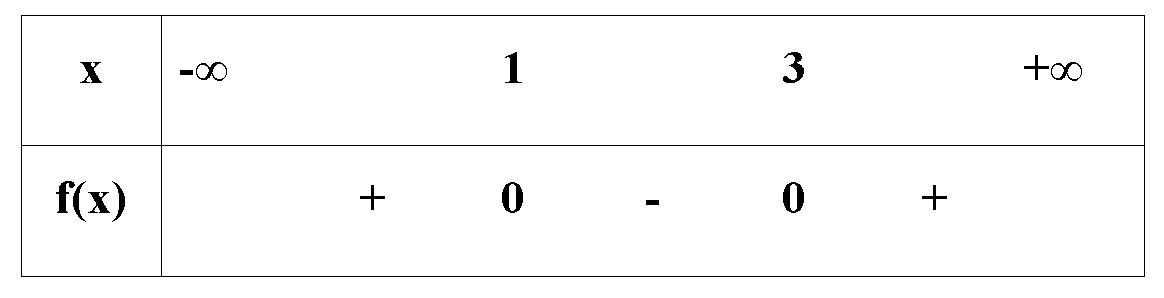
Lập bảng xét dấu của tam thức bậc hai f(x) = x² – 4x + 3.
Hướng dẫn giải
Tam thức bậc hai f(x) = x² – 4x + 3 có ∆ = b² – 4ac = (– 4)² – 4.1.3 = 4 > 0 có hai nghiệm phân biệt x₁ = 1; x₂ = 3;  hệ số a = 1 > 0.
Ta có bảng xét dấu như sau:

B. Bài tập tự luyện
B.1 Bài tập tự luận
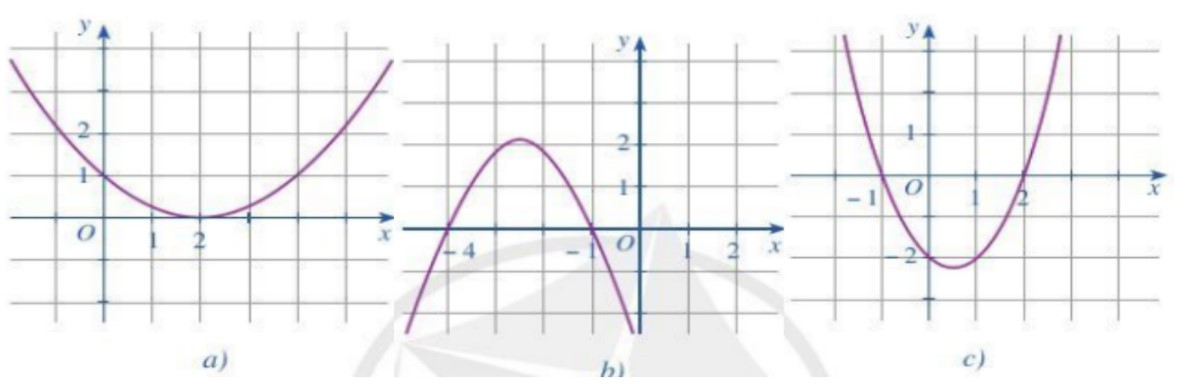
Bài 1. Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai với đồ thị được cho ở mỗi hình.

Hướng dẫn giải
a)
Ta thấy đồ thị cắt trục Ox tại điểm (2; 0) nên phương trình f(x) = 0 có duy nhất nghiệm x = 2.
Ta thấy đồ thị nằm trên trục hoành nên ta có bảng xét dấu:

b)
Ta thấy đồ thị cắt trục Ox tại hai điểm phân biệt (–4; 0) và (–1; 0) nên phương trình
f(x) = 0 có hai nghiệm phân biệt x₁ = –4; x₂ = –1.
Trong các khoảng (–∞; –4) và (–1; +∞) thì đồ thị nằm dưới trục hoành nên f(x) < 0, trong khoảng (–4; –1) thì đồ thị nằm trên trục hoành nên f(x) > 0.
Bảng xét dấu:

c)
Ta thấy đồ thị cắt trục Ox tại hai điểm phân biệt (–1; 0) và (2; 0) nên phương trình
f(x) = 0 có hai nghiệm phân biệt x₁ = –1; x₂ = 2
Trong các khoảng (–∞; –1) và (2; +∞) thì đồ thị nằm trên trục hoành nên f(x) > 0
Trong khoảng (–1; 2) thì đồ thị nằm dưới trục hoành nên f(x) < 0.
Bảng xét dấu:

Bài 2. Khi nào thì tam thức bậc hai $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^2+\left(\sqrt{5}-1\right)\mathrm{x}-\sqrt{5}$ nhận giá trị dương.
Hướng dẫn giải
Ta có: $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^2+\left(\sqrt{5}-1\right)\mathrm{x}-\sqrt{5}=0\iff \left[\begin{array}{l}\mathrm{x}=1\\ \mathrm{x}=-\sqrt{5}\end{array}\right.$.
Bảng xét dấu:

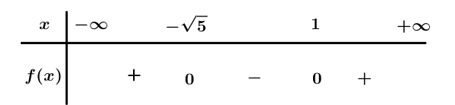
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)>0\iff \mathrm{x}\in \left(-\infty ;-\sqrt{5}\right)\cup \left(1;+\infty \right).$
Bài 3. Tìm giá trị nguyên của x để tam thức f(x) = 2x² – 7x – 9 nhận giá trị âm.
Hướng dẫn giải
Ta có: $\mathrm{f}\left(\mathrm{x}\right)=2{\mathrm{x}}^2-7\mathrm{x}-9=0\iff \left[\begin{array}{l}\mathrm{x}=-1\\ \mathrm{x}=\frac{9}{2}\end{array}\right.$ .
Bảng xét dấu

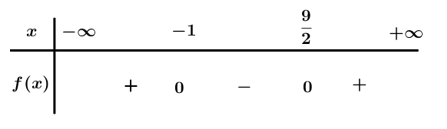
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)<0\iff -1<\mathrm{x}<\frac{9}{2}$.  Mà x nguyên nên x ∈ {0 ; 1 ; 2 ; 3 ; 4}.
Như vậy, với x nguyên x ∈ {0 ; 1 ; 2 ; 3 ; 4} thì f(x) = 2x² – 7x – 9  < 0. 
B.2 Bài tập trắc nghiệm
Câu 1.Tam thức bậc hai $\mathrm{f}\left(\mathrm{x}\right)=-{\mathrm{x}}^2+3\mathrm{x}-2$ nhận giá trị không âm khi và chỉ khi
A.$\mathrm{x}\in \left(-\infty ;1\right)\cup \left(2;+\infty \right)$;                 
B. $\mathrm{x}\in \left[1;2\right]$;       
C. $\mathrm{x}\in \left(-\infty ;1\right]\cup \left[2;+\infty \right)$.                 
D. $\mathrm{x}\in \left(1;2\right)$.
Hướng dẫn giải
Đáp án đúng là: B
Ta có: $\mathrm{f}\left(\mathrm{x}\right)=-{\mathrm{x}}^2+3\mathrm{x}-2=0\iff \left[\begin{array}{l}\mathrm{x}=1\\ \mathrm{x}=2\end{array}\right.$ .
Bảng xét dấu

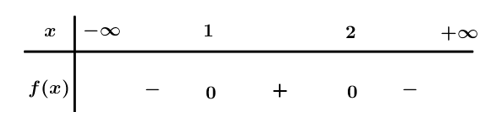
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)\ge 0\iff 1\le \mathrm{x}\le 2$.
Do đó, $\mathrm{x}\in \left[1;2\right]$.
Câu 2. Tam thức bậc hai $\mathrm{f}\left(\mathrm{x}\right)=-{\mathrm{x}}^2+5\mathrm{x}-6$ nhận giá trị dương khi và chỉ khi
A. $\mathrm{x}\in \left(-\infty ;2\right)$;     
B. $\left(3;+\infty \right)$;            
C. $\mathrm{x}\in \left(2;+\infty \right)$;     
D. $\mathrm{x}\in \left(2;3\right)$.
Hướng dẫn giải
Đáp án đúng là: D
Ta có: $\mathrm{f}\left(\mathrm{x}\right)=-{\mathrm{x}}^2+5\mathrm{x}-6=0\iff \left[\begin{array}{l}\mathrm{x}=2\\ \mathrm{x}=3\end{array}\right.$.
Bảng xét dấu

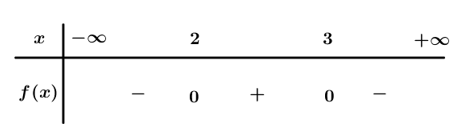
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)>0\iff \mathrm{x}\in \left(2;3\right).$ 
Câu 3. Cho các tam thức $\mathrm{f}\left(\mathrm{x}\right)=2{\mathrm{x}}^2-3\mathrm{x}+4;\mathrm{g}\left(\mathrm{x}\right)=-{\mathrm{x}}^2+3\mathrm{x}-4;\mathrm{h}\left(\mathrm{x}\right)=4-3{\mathrm{x}}^2$. Số tam thức đổi dấu trên ℝ là:
A. 0;   
B. 1;
C. 2;
D. 3.
Hướng dẫn giải
Đáp án đúng là: B
Vì f(x) = 0 vô nghiệm, g(x) = 0 vô nghiệm, h(x) = 0 có hai nghiệm phân biệt nên chỉ có h(x) đổi dấu trên ℝ.

Bài giảng Toán 10 Bài 3: Dấu của tam thức bậc hai – Cánh diều

====== ****&**** =====