Sách bài tập Toán 10 Bài 2 (Cánh diều): Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Giải SBT Toán lớp 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Giải SBT Toán 10 trang 47 Tập 1

Bài 9 trang 47 SBT Toán 10 Tập 1: Trong các hàm số sau, hàm số nào không là hàm số bậc hai?

A. y = – x² + 4x + 2;

B. y = x(2x² + 5x + 1);

C. y = – 3x(6x – 8);

D. y = x² + 6x.

Lời giải

Đáp án đúng là B

+) Hàm số y = – x² + 4x + 2 có dạng y = ax² + bx + c với a = – 1, b = 4 và c = 2. Do đó A là hàm số bậc hai.

+) Hàm số y = x(2x² + 5x + 1) = 2x³ + 5x² + x là hàm số bậc 3. Do đó B không là hàm số bậc hai.

+) Hàm số y = – 3x(6x – 8) = – 18x²  + 24x có dạng y = ax² + bx + c với a = – 18, b = 24 và c = 0. Do đó C là hàm số bậc hai.

+) Hàm số y = x² + 6x có dạng y = ax² + bx + c với a = 1, b = 6 và c = 0. Do đó C là hàm số bậc hai.

Bài 10 trang 47 SBT Toán 10 Tập 1: Cho hàm số f(x) = 2x² + 8x + 8. Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng (– 4; +∞), nghịch biến trên khoảng (–∞; – 4).

B. Hàm số đồng biến trên khoảng (– 2; +∞), nghịch biến trên khoảng (–∞; – 2).

C. Hàm số đồng biến trên khoảng (–∞; – 2), nghịch biến trên khoảng (– 2; +∞).

D. Hàm số đồng biến trên khoảng (–∞; – 4), nghịch biến trên khoảng (– 4; +∞).

Lời giải

Đáp án đúng là B

Hàm số f(x) = 2x² + 8x + 8 là hàm số bậc hai với a = 2 > 0, ∆ = 8² – 4.2.8 = 0.

Ta có: $-\frac{b}{2a}=-\frac{8}{2.2}=-2$; $-\frac{\Delta }{4a}=-\frac{0}{4.2}=0$

Ta có bảng biến thiên sau:

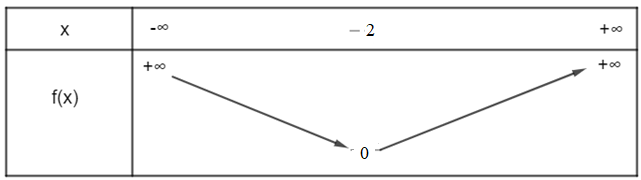
Vậy hàm số đồng biến trên khoảng (– 2; +∞), nghịch biến trên khoảng (–∞; – 2).

Bài 11 trang 47 SBT Toán 10 Tập 1: Xác định a, b, c lần lượt là hệ số của x², hệ số của x và hệ số tự do của các hàm số bậc hai sau:

a) f(x) = x² – x – 9;

b) f(x) = x² – 7;

c) f(x) = – 2x² + 8x.

Lời giải

a) Hàm số f(x) = x² – x – 9 là hàm số bậc hai có a = 1; b = – 1; c = – 9.

b) Hàm số f(x) = x² – 7 = x² + 0x – 7 là hàm số bậc hai có a = 1, b = 0 và c =  – 7.

c) Hàm số f(x) = – 2x² + 8x = – 2x² + 8x + 0 là hàm số bậc hai có a = – 2, b = 8 và c =  0.

Bài 12 trang 47 SBT Toán 10 Tập 1: Bố bạn Lan gửi 10 triệu đồng vào một ngân hàng với lãi suất x%/tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập với vốn ban đầu để tính lãi cho tháng tiếp theo. Tính số tiền cả vốn và lãi mà bố Lan có được sau khi gửi tiết kiệm 2 tháng?

Lời giải

Tiền cả gốc lẫn lãi bố Lan nhận được sau tháng thứ nhất là:

10 + x%.10 = 10 + 0,1x (triệu đồng).

Tiền cả gốc lẫn lãi bố Lan nhận được sau tháng thứ hai là:

10 + 0,1x + (10 + 0,1x).0,01x = 0,001x² + 0,2x + 10 (triệu đồng).

Vậy số tiền cả vốn và lãi mà bố Lan có được sau khi gửi tiết kiệm 2 tháng là: 0,001x² + 0,2x + 10 (triệu đồng).

Bài 13 trang 47 SBT Toán 10 Tập 1: Xác định parabol y = ax² – bx + 1 trong mỗi trường hợp sau:

a) Đi qua hai điểm M(1; – 2) và N(– 2; 19).

b) Có đỉnh I(– 2; 37).

c) Có trục đối xứng là x = – 1 và tung độ của đỉnh bằng 5.

Lời giải

Xét parabol y = ax² – bx + 1 với a ≠ 0:

a) Thay tọa độ điểm M1; – 2) vào parabol y = ax² – bx + 1, ta được:

– 2 = a.1² – b.1 + 1 ⇔ a – b = – 3 (1).

Thay tọa độ điểm N(– 2; 19) vào parabol y = ax² – bx + 1, ta được:

 19 = a.(– 2)² – b.(– 2) + 1 ⇔ 4a + 2b = 18 hay 2a + b = 9 (2).

Từ (1) và (2) ta có hệ phương trình:

$\left\{\begin{array}{l}a-b=-3\\ 2a+b=9\end{array}\right.\iff \left\{\begin{array}{l}3a=6\\ 2a+b=9\end{array}\right.\iff \left\{\begin{array}{l}a=2\\ 2.2+b=9\end{array}\right.\iff \left\{\begin{array}{l}a=2\\ b=5\end{array}\right.$ (thỏa mãn điều kiện).

Vậy parabol cần tìm là y = 2x² – 5x + 1.

b) Parabol có đỉnh I(– 2; 37) nghĩa là $\frac{b}{2a}=-2$ ⇔ b = – 4a (3)

Mặt khác ta thay tọa độ điểm I vào parabol y = ax² – bx + 1, ta được:

37 = a.(– 2)² – b.(– 2) + 1 ⇔ 4a + 2b = 36 hay 2a + b = 18 (4).

Từ (3) và (4) ta có hệ phương trình:

$\left\{\begin{array}{l}b=-4a\\ 2a+b=18\end{array}\right.\iff \left\{\begin{array}{l}b=-4a\\ 2a-4a=18\end{array}\right.\iff \left\{\begin{array}{l}b=-4a\\ -2a=18\end{array}\right.\iff \left\{\begin{array}{l}b=36\\ a=-9\end{array}\right.$ (thỏa mãn điều kiện).

Vậy parabol cần tìm là: y = – 9x² – 36x + 1.

c) Parabol có trục đối xứng là x = – 1 ⇔ $\frac{b}{2a}=-1$ ⇔ b = – 2a (5)

Thay x = – 1 và y = 5 vào parabol y = ax² – bx + 1, ta được:

5 = a.(– 1)² – b.(– 1) + 1 ⇔ a + b = 4 (6).

Từ (5) và (6) ta có hệ phương trình:

$\left\{\begin{array}{l}b=2a\\ a+b=4\end{array}\right.\iff \left\{\begin{array}{l}b=-2a\\ a-2a=4\end{array}\right.\iff \left\{\begin{array}{l}b=-2a\\ -a=4\end{array}\right.\iff \left\{\begin{array}{l}b=8\\ a=-4\end{array}\right.$ (thỏa mãn điều kiện).

Vậy parabol cần tìm là: y = – 4x² – 8x + 1.

Bài 14 trang 47 SBT Toán 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:

a) y = 3x² – 4x + 2;

b) y = – 2x² – 2x – 1.

Lời giải

a) Hàm số y = 3x² – 4x + 2, có a = 3, b = – 4, c = 2 và ∆ = (– 4)² – 4.3.2 = – 8 < 0.

– Tọa độ điểm đỉnh là: x_I = $-\frac{b}{2a}=-\frac{-4}{2.3}=\frac{2}{3}$ và y_I = $-\frac{\Delta }{4a}=-\frac{-8}{4.3}=\frac{2}{3}$

⇒ $I\left(\frac{2}{3};\frac{2}{3}\right)$.

– Trục đối xứng $x=\frac{2}{3}$.

– Parabol không cắt trục hoành.

– Parabol cắt trục tung tại điểm có tọa độ (0; 2) và điểm đối xứng với điểm này qua trục đối xứng có tọa độ $\left(\frac{4}{3};2\right)$.

– Ta có a = 3 > 0 nên bề lõm của parabol hướng lên trên.

Đồ thị hàm số parabol đã cho là:

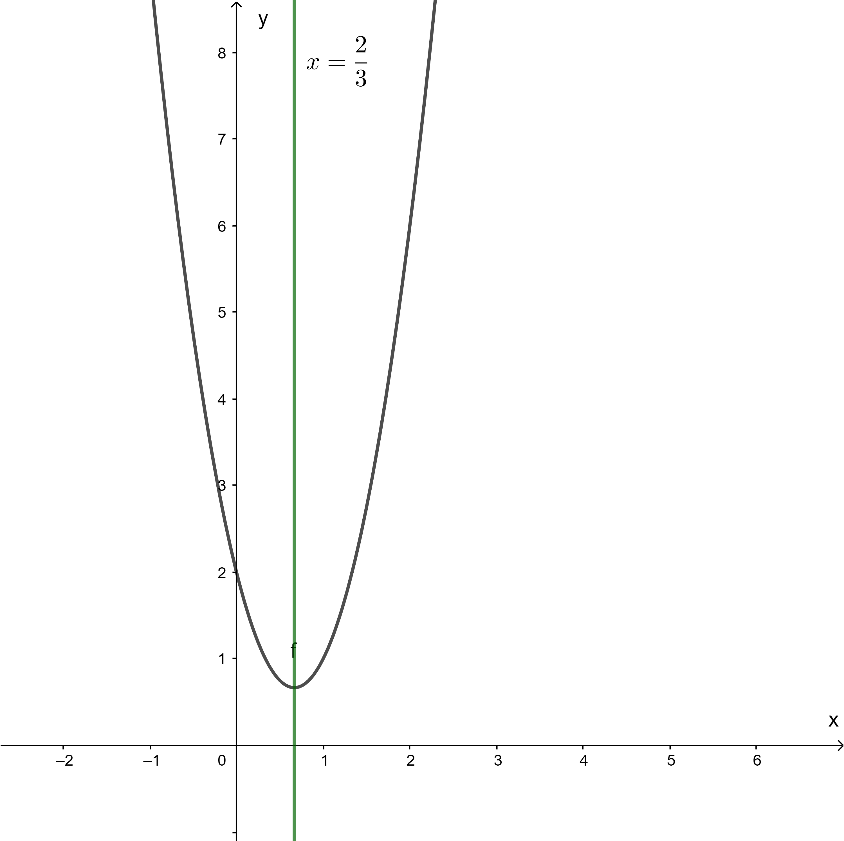
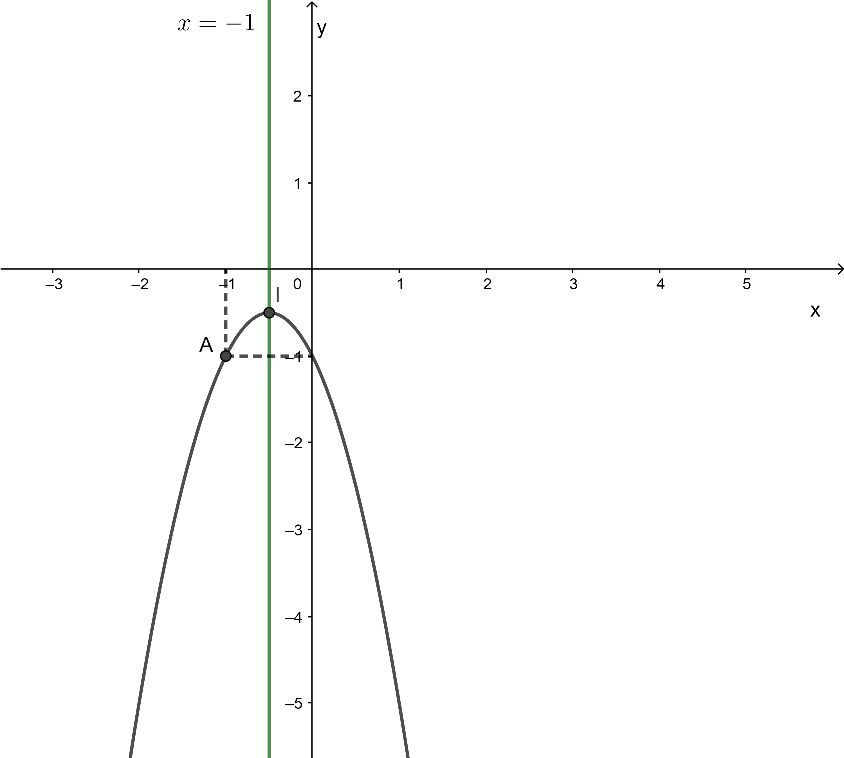
b) Hàm số y = – 2x² – 2x – 1, có a = – 2 , b = – 2, c = – 1 và ∆ = (– 2)² – 4.(– 2).(– 1) = – 5 < 0.

– Tọa độ điểm đỉnh là: x_I = $-\frac{b}{2a}=-\frac{-2}{2.(-2)}=-\frac{1}{2}$ và y_I = $-\frac{\Delta }{4a}=-\frac{-4}{4.(-2)}=-\frac{1}{2}$

⇒ $I\left(-\frac{1}{2};-\frac{1}{2}\right)$.

– Trục đối xứng $x=-\frac{1}{2}$.

– Parabol không cắt trục hoành.

– Parabol cắt trục tung tại điểm có tọa độ (0; – 1) và điểm đối xứng với điểm này qua trục đối xứng có tọa độ A$\left(-1;-1\right)$.

– Ta có a = – 2 < 0 nên bề lõm của parabol hướng xuống dưới.

Đồ thị hàm số parabol đã cho là:

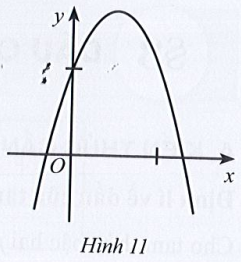
Bài 15 trang 47 SBT Toán 10 Tập 1: Cho hàm số y = ax² + bx + c có đồ thị ở Hình 11. Xác định dấu a, b, c.

Lời giải

Hàm số đã cho có đồ thị là đường cong parabol:

Parabol có bề lõm hướng xuống dưới nên a < 0.

Đồ thị hàm số cắt trục tung tại điểm có tung độ nằm phía trên trục hoành nên c > 0.

Trục đối xứng của hàm số nằm bên phải trục tung nên $-\frac{b}{2a}>0$

Mà a < 0 nên – b < 0 hay b > 0.

Vậy a < 0, b > 0 và c > 0.

Giải SBT Toán 10 trang 48 Tập 1

Bài 16 trang 48 SBT Toán 10 Tập 1: Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:

a) y = 4x² + 6x – 5;

b) y = – 3x² + 10x – 4.

Lời giải

a) Hàm số y = 4x² + 6x – 5, có a = 4 > 0 và ∆ = 6² – 4.4.(– 5) =  116

Ta có $-\frac{b}{2a}=-\frac{6}{2.4}=-\frac{3}{4}$ và $-\frac{\Delta }{4a}=-\frac{116}{4.4}=-\frac{29}{4}$

Khi đó, ta có bảng biến thiên:

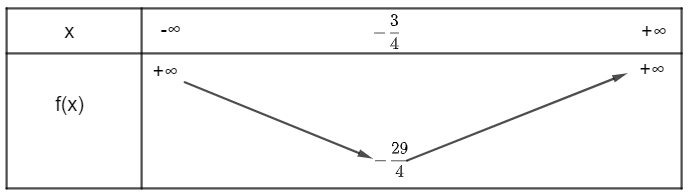
Vậy hàm số nghịch biến trên $\left(-\infty ;-\frac{3}{4}\right)$, hàm số đồng biến trên $\left(-\frac{3}{4};+\infty \right)$.

b) Hàm số y = – 3x² + 10x – 4, có a = – 3 < 0 và ∆ = 10² – 4.(– 3).(– 4) = 52

Ta có $-\frac{b}{2a}=-\frac{10}{2.(-3)}=\frac{5}{3}$ và $-\frac{\Delta }{4a}=-\frac{52}{4.(-3)}=\frac{13}{3}$

Khi đó, ta có bảng biến thiên:

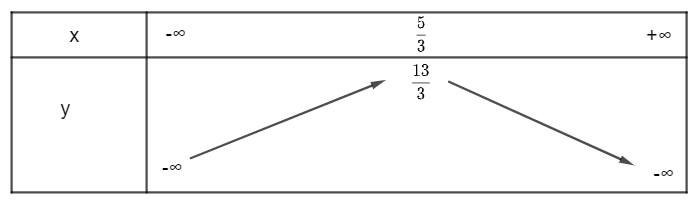
Vậy hàm số đồng biến trên $\left(-\infty ;\frac{5}{3}\right)$, hàm số nghịch biến trên $\left(\frac{5}{3};+\infty \right)$.

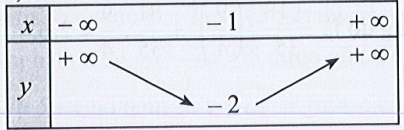
Bài 17 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết hệ số tự do c = 2 và bảng biến thiên tương ứng trong mỗi trường hợp sau:

a)

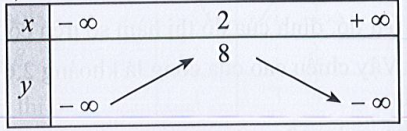
b)

Lời giải

a) Dựa vào bảng biến thiên ta có:

$-\frac{b}{2a}=-1$ ⇔ b = 2a

$-\frac{\Delta }{4a}=-2$ ⇔ ∆ = 8a ⇔ b² – 4ac = 8a

⇔ (2a)² – 4a.2 = 8a

⇔ 4a² – 8a = 8a

⇔ 4a² – 16a = 0

⇔ 4a(a – 4) = 0

⇔ a = 0 (không thỏa mãn) hoặc a = 4 (thỏa mãn)

⇒ b = 2a = 2.4 = 8.

Vậy hàm số bậc hai cần tìm là y = 4x² + 8x + 2.

b) Dựa vào bảng biến thiên ta có:

$-\frac{b}{2a}=2$ ⇔ b = – 4a

$-\frac{\Delta }{4a}=8$ ⇔ ∆ = – 32a ⇔ b² – 4ac = – 32a

⇔ (4a)² – 4a.2 = – 32a  

⇔ 4a² – 8a = – 32a

⇔ 16a² + 24a = 0

⇔ 8a(2a + 3) = 0

⇔ a = 0 (không thỏa mãn) hoặc a = $\frac{–3}{2}$ (thỏa mãn)

⇒ b = – 4a = – 4.$\left(\frac{–3}{2}\right)$ = 6.

Vậy hàm số bậc hai cần tìm là y = $-\frac{3}{2}$x² + 6x + 2.

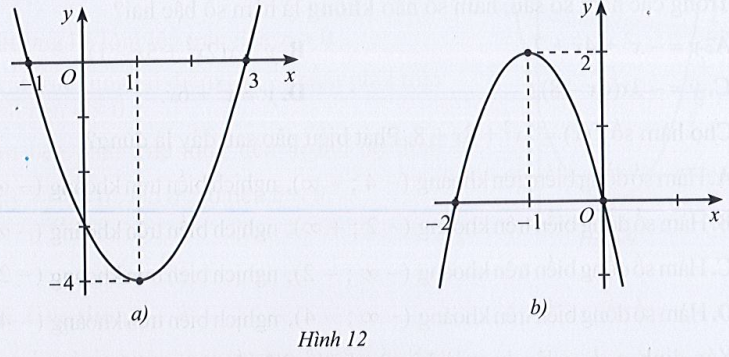
Bài 18 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b:

Lời giải

+) Hình 12a):

Dựa vào hình vẽ, ta thấy:

– Đồ thị hàm số cắt trục tung tại điểm có tung độ – 3 nên c = – 3.

– Điểm đỉnh của parabol có tọa độ (1; – 4) nên ta có:

$-\frac{b}{2a}=1$ ⇔ b = – 2a

$-\frac{\Delta }{4a}=-4$⇔ ∆ = 16a

⇔ b² – 4ac = 16a

⇔ (– 2a)² – 4a(– 3) = 16a

⇔ 4a² + 12a = 16a

⇔ 4a² – 4a = 0

⇔ 4a(a – 1) = 0

⇔ a = 0 (không thỏa mãn) hoặc a = 1 (thỏa mãn)

⇒ b = – 2a = – 2.1 = – 2.

Vậy hàm số bậc hai cần tìm là y = x² – 2x – 3.

+) Hình 12b):

Dựa vào hình vẽ, ta thấy:

– Đồ thị hàm số cắt trục tung tại điểm có tung độ 0 nên c = 0.

– Điểm đỉnh của parabol có tọa độ (– 1; 2) nên ta có:

$-\frac{b}{2a}=-1$ ⇔ b = 2a

$-\frac{\Delta }{4a}=2$⇔ ∆ = – 8a

⇔ b² – 4ac = – 8a

⇔ (2a)² – 4a.0 = – 8a

⇔ 4a² = – 8a

⇔ 4a² + 8a = 0

⇔ 4a(a + 2) = 0

⇔ a = 0 (không thỏa mãn) hoặc a = – 2 (thỏa mãn)

⇒ b = 2a = 2.(– 2) = – 4.

Vậy hàm số bậc hai cần tìm là y = – 2x² – 4x.

Bài 19 trang 48 SBT Toán 10 Tập 1: Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m. Từ một điểm M trên thân cổng người ta đo được khoảng cách tới mặt đất là MK = 1,6 m và khoảng cách từ K tới chân cổng gần nhất là BK = 0,5 m. Tính chiều cao của cổng theo đơn vị mét (làm tròn kết quả đến hàng phần mười).

Lời giải

Đặt hệ trục tọa độ như hình vẽ:

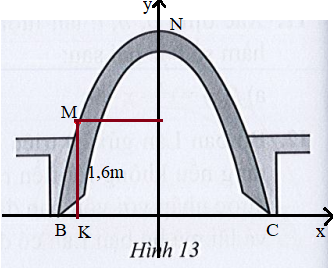
Tọa độ các điểm lần lượt là: B(– 4,5; 0); C(4,5; 0);

Vì BK = 0,5 m nên OK = 4,5 – 0,5 = 4 m. Do đó M(4; 1,6).

Cổng có hình parabol nên gọi phương trình hàm số là y = ax² + bx + c (a ≠ 0) (1).

Điểm B thuộc parabol nên thay tọa độ điểm B vào (1) ta được:

0 = a(– 4,5)² + b(– 4,5) + c ⇔ 20,25a – 4,5b + c = 0 (2).

Điểm C thuộc parabol nên thay tọa độ điểm C vào (1) ta được:

0 = a(4,5)² + b(4,5) + c ⇔ 20,25a + 4,5b + c = 0 (3).

Điểm M thuộc parabol nên thay tọa độ điểm M vào (1) ta được:

1,6 = a.4² + b.4 + c ⇔ 16a + 4b + c = 1,6 (4).

Từ (2), (3) và (4) ta có hệ phương trình: $\left\{\begin{array}{l}20,25a-4,5b+c=0\\ 20,25a+4,5b+c=0\\ 16a+4b+c=1,6\end{array}\right.\iff \left\{\begin{array}{l}a=-\frac{32}{85}\\ b=0\\ c=\frac{648}{85}\end{array}\right.$.

Suy ra parabol cần tìm là: y = $-\frac{32}{85}$x² + $\frac{648}{85}$.

Điểm N là điểm đỉnh của parabol thuộc vào trục tung Oy nên hoành độ điểm N bằng 0.

Thay x = 0 vào hàm số y = $-\frac{32}{85}$x² + $\frac{648}{85}$, ta được y = $-\frac{32}{85}$.0² + $\frac{648}{85}$ = $\frac{648}{85}$.

⇒ N$\left(0;\frac{648}{85}\right)$.

Tung độ điểm N cũng chính là chiều cao của cổng và bằng $\frac{648}{85}\approx 7,6$ m.

Vậy chiều cao của cổng khoảng 7,6 m.

Bài giảng Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai – Cánh diều

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài 1: Hàm số và đồ thị

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc nhất một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

====== ****&**** =====