Cho biểu thức:  A = sin2(a + b) – sin2a – sin2b. Đưa biểu thức trên về dạng tích:

Câu hỏi:

Cho biểu thức:  A = sin²(a + b) – sin²a – sin²b. Đưa biểu thức trên về dạng tích:

A. A = 2cosa. sinb.sin( a + b)

B. A = 2.sina.cosb.cos(a + b)

C. A = 2cosa.cosb.cos(a + b)

D. A = 2sina.sinb.cos( a + b)

Đáp án chính xác

Trả lời:

Chọn D.
Ta có: A = sin²(a + b) –sin²a – sin²b
= ( sina.cosb + cosa.sinb) ² – sin²a – sin²b
= sin²a.cos²b + 2sina.cosb.cosa.sinb + cos²a.sin²b – sin ²a – sin²b
= sin²a( cos²b – 1) + sin²b( cos²a – 1) + 2.sina.cosa.sinb.cosb
= – sin²a.sin²b – sin²b.sin²a + 2.sina.cosa.sinb.cosb
= 2sina.sinb( cosa.cosb – sina.sinb) = 2.sina.sinb.cos( a + b).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hai góc nhọn a và b với tan a = 1/7 và tan b = 3/4. Tính tổng 2 góc đó?
   
   

   Câu hỏi:
   

   Cho hai góc nhọn a và b với tan a = 1/7 và tan b = 3/4. Tính tổng 2 góc đó?

   

   

   Đáp án chính xác

   

   

   Trả lời:

   Chọn B.
    
   Theo công thức cộng ta có:
   
   Mà a và b là các góc nhọn suy ra 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho x và y là các góc nhọn, cotx = 3/4, cot y = 1/7. Tổng 2 góc đó là:
   
   

   Câu hỏi:
   

   Cho x và y là các góc nhọn, cotx = 3/4, cot y = 1/7. Tổng 2 góc đó là:

   A. $\frac{\mathrm{\pi }}{4}$

   B. $\frac{3\mathrm{\pi }}{4}$

   Đáp án chính xác

   C. $\frac{\mathrm{\pi }}{3}$

   D. $\mathrm{\pi }$

   Trả lời:

   Chọn B.
   Theo giả thiết cotx = 3/4, cot y = 1/7 nên tan x = 4/3 và tan y = 7
   Theo công thức cộng ta có :
   
   Mà x và y lại là các góc nhọn suy ra 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tính giá trị của biểu thức  bằng :
   
   

   Câu hỏi:
   

   Tính giá trị của biểu thức 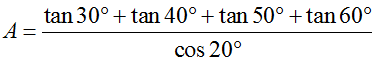 bằng :

   

   

   

   

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Ta có:
   
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Giá trị của biểu thức  bằng :
   
   

   Câu hỏi:
   

   Giá trị của biểu thức 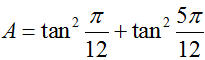 bằng :

   A. 14

   Đáp án chính xác

   B. 16

   C. 18

   D. 20

   Trả lời:

   Chọn A.
   Ta có: 
   
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Rút gọn biểu thức C = 2( sin4x + cos4x + sin2x.cos2x) 2 – ( sin8x + cos8x)  có giá trị không đổi và bằng
   
   

   Câu hỏi:
   

   Rút gọn biểu thức C = 2( sin⁴x + cos⁴x + sin²x.cos²x) ² – ( sin⁸x + cos⁸x)  có giá trị không đổi và bằng

   A. 2

   B. 4

   C. 1

   Đáp án chính xác

   D. 0

   Trả lời:

   Chọn C.
   Ta có: C = 2( sin⁴x + cos⁴x + sin²x.cos²x) ² – ( sin⁸x + cos⁸x)
   = 2 [ (sin²x + cos²x) ² – sin²x.cos²x]² – [ (sin⁴x + cos⁴x)² – 2sin⁴x.cos⁴x]
   = 2[ 1 – sin²x.cos²x]² – [ (sin²x+ cos²x) ² – 2sin²x.cos²x]² + 2sin⁴x.cos⁴x
   = 2[ 1- sin²x.cos²x]² – [ 1 – 2sin²x.cos²x]²  + 2sin⁴x.cos⁴x
   = 2( 1 – 2sin²xcos²x+ sin⁴x.cos⁴x) –( 1- 4sin²xcos²x+ 4sin⁴xcos⁴x) + 2sin⁴x.cos⁴x
   =  1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====