Cho hình bình hành ABCD. Phép tịnh tiến TDA→ biến:

Câu hỏi:

Cho hình bình hành ABCD. Phép tịnh tiến $T_{\overrightarrow{DA}}$ biến:

A. B thành C

B. C thành A

C. C thành B

Đáp án chính xác

D. A thành D

Trả lời:

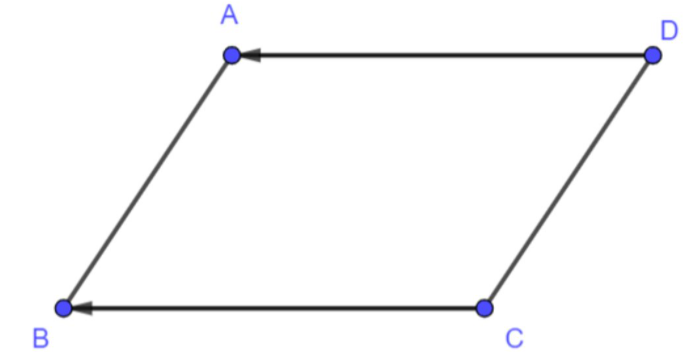Theo đề bài, ABCD là hình bình hành$\Rightarrow \overrightarrow{DA}=\overrightarrow{CB}$$\Rightarrow T_{\overrightarrow{DA}}\left(C\right)=B$.Đáp án C.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình bình hành ABCD. Phép tịnh tiến TAB→ + AD→ biến điểm A thành điểm:
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD. Phép tịnh tiến $T_{\overrightarrow{AB} + \overrightarrow{AD}}$ biến điểm A thành điểm:

   A. A’ đối xứng với A qua C

   B. A’ đối xứng với D qua C

   C.O là giao điểm của AC và BD

   D. C

   Đáp án chính xác

   Trả lời:

   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho đường tròn (C) có tâm O và đường kính AB. Gọi ∆ là tiếp tuyến của (C) tại điểm A. Phép tịnh tiến TAB⇀ biến ∆ thành:
   
   

   Câu hỏi:
   

   Cho đường tròn (C) có tâm O và đường kính AB. Gọi ∆ là tiếp tuyến của (C) tại điểm A. Phép tịnh tiến $T_{\stackrel{\rightharpoonup }{AB}}$ biến ∆ thành:

   A. Đường kính của (C) song song với ∆.

   B. Tiếp tuyến của (C) tại điểm B.

   Đáp án chính xác

   C. Tiếp tuyến của (C) song song với AB.

   D. Đường kính của (C) qua O.

   Trả lời:

   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho v→(-1;5) và điểm M’(4;2). Biết M’ là ảnh của M qua phép tịnh tiến Tv→ . Tìm M.
   
   

   Câu hỏi:
   

   Cho $\overrightarrow{v}(–1;5)$ và điểm M’(4;2). Biết M’ là ảnh của M qua phép tịnh tiến $T\overrightarrow{v}$ . Tìm M.

   A. M(5; -3)

   Đáp án chính xác

   B. M(-3;5)

   C. M(3; 7)

   D. M(-4;10)

   Trả lời:

   Sử dụng biểu thức tọa độ của phép tịnh tiếnĐáp án A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho v→(3;3) và đường tròn (C): x2 + y2 – 2x + 4y – 4 = 0. ảnh của (C) qua Tv→ là (C’).
   
   

   Câu hỏi:
   

   Cho v→(3;3) và đường tròn (C): $x^2 + y^2 – 2x + 4y – 4 = 0$. ảnh của (C) qua Tv→ là (C’).

   A. ${\left(x – 4\right)}^2 + {\left(y – 1\right)}^2 = 4$

   B. ${\left(x – 4\right)}^2 + {\left(y – 1\right)}^2 = 9$

   Đáp án chính xác

   C. ${\left(x + 4\right)}^2 + {\left(y – 1\right)}^2 = 9$

   D. $x^2 + y^2 + 8x + 2y – 4 = 0$

   Trả lời:

   Tịnh tiến tâm đường tròn, bán kính không thay đổi.Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho v→(-4;2) và đường thẳng ∆':2x – y – 5 = 0. Hỏi ∆' là ảnh của đường thẳng ∆ nào qua Tv→
   
   

   Câu hỏi:
   

   Cho $\overrightarrow{v}(–4;2)$ và đường thẳng ∆’:2x – y – 5 = 0. Hỏi ∆’ là ảnh của đường thẳng ∆ nào qua $T\overrightarrow{v}$

   A. ∆:2x – y – 13 = 0

   B. ∆:x – 2y – 9 = 0

   C. ∆:2x + y – 15 = 0

   D. ∆:2x – y -15 = 0

   Đáp án chính xác

   Trả lời:

   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====