Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 7 Cánh diều bản word có lời giải chi tiết ( cho 1 đề thi bất kì):
B1: –
B2: – nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Bộ 10 đề thi học kì 2 Toán lớp 7 Cánh diều có đáp án năm 2023 – 2024 – Đề 1
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2 – Cánh diều
Năm học 2023 – 2024
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 1)
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Trong chuyến du lịch tại Đà Nẵng, Nhi quen được một người bạn mới cũng là người Việt Nam nhưng lại quên quê hương của người bạn ấy. Hỏi có tất cả bao nhiêu tỉnh thành có thể là quê hương của người bạn mới đó?
A. 43; B. 53; C. 63; D. 73.
Câu 2: Tỉ lệ phần trăm các loại trái cây được giao cho cửa hàng A được biểu diễn bằng biểu đồ:
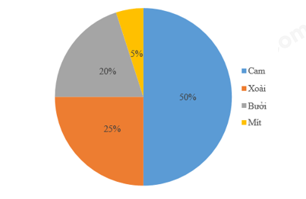
Số lượng cam được giao gấp bao nhiêu lần số lượng mít?
A. 5 lần; B. 10 lần; C. 15 lần; D. 20 lần.
Câu 3. Cho , hai đường phân giác BD và CE cắt nhau tại , thế thì:
A. .
B. .
C. .
D. .
Câu 4: Gọi là giao điểm của ba đường phân giác của tam giác thì:
A. cách đều ba cạnh của tam giác.
B. là trọng tâm của tam giác.
C. cách đều ba đỉnh của tam giác.
D. là trực tâm của tam giác.
Câu 5: Tính chất nào sau đây không phải của tam giáccân tại :
A. Trung tuyến và của tam giác bằng nhau.
B. .
C. .
D.
Câu 6. Cho dãy số liệu về cân nặng (theo đơn vị kilogam) của 15 học sinh lớp 7 như sau: 40, 39, 41, 45, 41, 42, 40, 42, 40, 41, 43, 40, 42, 45, 42. Chọn ngẫu nhiên 1 bạn trong 15 bạn này. Tính xác suất của biến cố “Bạn được chọn có cân nặng là 45 kg”.
A. B. C. D.
Câu 7. Cho hình vẽ sau:
Em hãy chọn đáp án sai trong các đáp án sau:
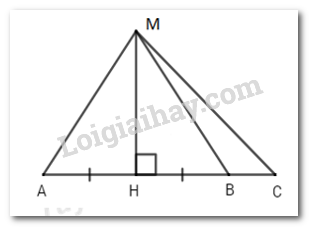
A. B. C. D.
Câu 8. Cho hai đa thức . Giá trị của tại x = -1 là:
A. –8
B. –12
C. 10
D. 18
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm)
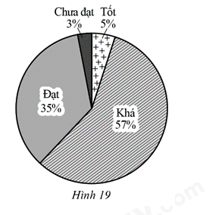
Kết quả học tập Học kì I của học sinh lớp 7A được đánh giá ở bốn mức: Tốt, Khá, Đạt, Chưa đạt. Biểu đồ hình quạt tròn ở Hình 19 biểu diễn kết quả học tập Học kì I (tỉnh theo tỉ số phần trăm) của học sinh lớp 7A theo bốn mức trên
a) Có bao nhiêu phần trăm học sinh lớp 7A có kết quả học tập Học kì I được đánh giá ở mức Tốt? Mức Khá? Mức Đạt? Mức Chưa đạt?
b) Tổng số học sinh có kết quả học tập Học kì I được đánh giả ở mức Đạt và Chưa đạt bằng bao nhiêu phần trăm tổng số học sinh có kết quả học tập được đánh giá ở mức Tốt và Khá (làm tròn kết quả đến hàng phần mười)?
Bài 2. (2,5 điểm) Cho hai đa thức sau:
a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến.
b) Tính .
c) Tìm nghiệm của đa thức .
Bài 3. (3,5 điểm) Cho tam giácvuông tạivà có đường phân giác . Kẻ đường thẳng vuông có với tại điểm . Trên tia đối của tia lấy điểm sao cho .
a) Chứng minh rằng .
b) Chứng minh rằng: Đường thẳng là đường trung trực của đoạn thẳng và .
c) Chứng minh rằng: Ba điểm thẳng hàng và đường thẳng vuông góc với đường thẳng .
d) Chứng minh rằng:
Cho cân tại , tia phân giác của cắt cạnh tại . Kẻ vuông góc với tại , kẻ vuông
Bài 5. (0,5 điểm) Cho đa thức thỏa mãn với mọi giá trị của
A. Ma trận 1 đề thi Học kì 2 môn Toán lớp 7 (Cánh diều)
|
STT |
Chương |
Nội dung kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Tổng % điểm |
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||||||
|
TN |
TL |
TN |
TL |
TN |
TL |
TN |
TL |
||||
|
1 |
Một số yếu tố thống kê và xác suất |
Thống kê – Thu thập và tổ chức dữ liệu |
|
|
2 (0,5đ) |
1 (0,5đ) |
|
1 (0,5đ) |
|
|
25% |
|
Xác suất – Làm quen với biến cố ngẫu nhiên và xác suất của biến cố ngẫu nhiên |
2 (0,5đ) |
|
|
1 (0,5đ) |
|
|
|
|
|||
|
2 |
Biểu thức đại số |
Biểu thức đại số |
|
|
1 (0,25đ) |
|
|
|
|
|
35% |
|
Đa thức một biến |
2 (0,5đ) |
1 (0,5đ) |
|
2 (1,0đ) |
|
1 (0,5đ) |
|
1 (0,5đ) |
|||
|
3 |
Tam giác |
Tam giác. Tam giác bằng nhau. Tam giác cân. Quan hệ giữa đường vuông góc và đường xiên. Các đường đồng quy của tam giác |
4 (1,0đ) |
|
|
1 (1,0đ) |
|
2 (2,0đ) |
|
|
40% |
|
Tổng: Số câu Điểm |
8 (2,0đ) |
1 (0,5đ) |
4 (1,0đ) |
5 (3,0đ) |
|
4 (3,0đ) |
|
1 (0,5đ) |
23 (10đ) |
||
|
Tỉ lệ |
25% |
40% |
30% |
5% |
100% |
||||||
|
Tỉ lệ chung |
65% |
35% |
100% |
||||||||
Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ nhận biết, thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 2
|
STT |
Chương |
Nội dung kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Số câu hỏi theo mức độ |
|||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
1 |
Một số yếu tố thống kê và xác suất |
Thống kê – Thu thập và tổ chức dữ liệu |
Nhận biết: – Nhận biết được những dạng biểu diễn khác nhau cho một tập dữ liệu. Thông hiểu: – Thực hiện và lí giải được việc thu thập, phân loại dữ liệu theo các tiêu chí cho trước từ những nguồn: văn bản, bảng biểu, kiến thức trong các môn học khác và trong thực tiễn. – Giải thích được tính hợp lí của dữ liệu theo các tiêu chí toán học đơn giản (ví dụ: tính hợp lí, tính đại diện của một kết luận trong phỏng vấn; tính hợp lí của các quảng cáo; …) – Đọc và mô tả được các dữ liệu ở dạng biểu đồ thống kê: biểu đồ hình quạt tròn, biểu đồ đoạn thẳng. Vận dụng: – Lựa chọn và biểu diễn dữ liệu vào bảng, biểu đồ thích hợp biểu đồ thống kê: biểu đồ hình quạt tròn, biểu đồ đoạn thẳng. – Nhận ra được vấn đề hoặc quy luật đơn giản dựa trên phân tích các số liệu thu được ở dạng: biểu đồ hình quạt tròn, biểu đồ đoạn thẳng. – Giải quyết được những vấn đề đơn giản liên quan đến các số liệu thu được ở dạng: biểu đồ hình quạt tròn, biểu đồ đoạn thẳng. |
|
2TN, 1TL |
1TL |
|
|
Xác suất – Làm quen với biến cố ngẫu nhiên và xác suất của biến cố ngẫu nhiên |
Nhận biết: – Nhận biết biến cố chắc chắn, biến cố không thể, biến cố ngẫu nhiên. – Nhận biết được xác suất của một biến cố ngẫu nhiên. Thông hiểu: – Tính toán được xác suất của một biến cố ngẫu nhiên trong một số ví dụ đơn giản (ví dụ: lấy bóng trong túi, tung xúc xắc,…). |
2TN |
1TL |
|
|
||
|
2 |
Biểu thức đại số và đa thức |
Biểu thức đại số |
Nhận biết: – Nhận biết được biểu thức số. – Nhận biết được biểu thức đại số. – Xác định biến số (biến) trong một biểu thức đại số. Thông hiểu: – Tính được giá trị của một biểu thức đại số. – Viết một biểu thức đại số biểu thị một mệnh đề. |
|
2TN |
|
|
|
Đa thức một biến |
Nhận biết: – Nhận biết đơn thức một biến và bậc của đơn thức. – Nhận biết đa thức một biến và các hạng tử của nó. – Nhận biết bậc, hệ số cao nhất, hệ số tự do của đa thức một biến. – Nhận biết được nghiệm của đa thức một biến. Thông hiểu: – Thu gọn và sắp xếp các hạng tử của một đa thức. – Tính được giá trị của đa thức khi biết giá trị của biến. – Xác định một số có phải nghiệm của đa thức một biến không. Vận dụng: – Thực hiện được các phép tính: phép cộng, phép trừ phép nhân, phép chia trong tập hợp các đa thức một biến; vận dụng được những tính chất của các phép tính đó trong tính toán. – Tìm nghiệm của đa thức một biến. Vận dụng cao: – Xác định được hệ số của đa thức một biến để đa thức thỏa mãn yêu cầu. – Vận dụng tính chất của phép chia đa thức một biến để giải toán. |
2TN, 1TL |
2TL |
1TL |
1TL |
||
|
3 |
Quan hệ giữa các yếu tố trong một tam giác |
Tam giác. Tam giác bằng nhau. Tam giác cân. Quan hệ giữa đường vuông góc và đường xiên. Các đường đồng quy của tam giác |
Nhận biết: – Nhận biết liên hệ về độ dài của ba cạnh trong một tam giác. – Nhận biết được khái niệm hai tam giác bằng nhau. – Nhận biết tam giác cân. – Nhận biết đường vuông góc và đường xiên; khoảng cách từ một điểm đến một đường thẳng. – Nhận biết đường trung trực của một đoạn thẳng và tính chất cơ bản của đường trung trực. – Nhận biết các đường đặc biệt trong tam giác (đường trung tuyến, đường cao, đường phân giác, đường trung trực); sự đồng quy của các đường đặc biệt đó. Thông hiểu: – Giải thích được định lí về tổng các góc trong một tam giác bằng . – Tính số đo của một góc dựa vào định lí tổng ba góc của một tam giác. – Giải thích được các trường hợp bằng nhau của hai tam giác, của hai tam giác vuông. – Mô tả được tam giác cân và giải thích được tính chất của tam giác cân. – Giải thích được quan hệ giữa đường vuông góc và đường xiên dựa trên mối quan hệ giữa cạnh và góc đối trong tam giác (đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại). – Giải thích, mô tả tính chất của các đường đặc biệt và sự đồng quy của các đường đặc biệt đó trong tam giác (đường trung tuyến, đường cao, đường phân giác, đường trung trực). Vận dụng: – Diễn đạt được lập luận và chứng minh hình học trong những trường hợp đơn giản (ví dụ: lập luận và chứng minh được các đoạn thẳng bằng nhau, các góc bằng nhau từ các điều kiện ban đầu liên quan đến tam giác,…). – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) liên quan đến ứng dụng của hình học như: đo, vẽ, tạo dựng các hình đã học. Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) liên quan đến ứng dụng của hình học như: đo, vẽ, tạo dựng các hình đã học. |
4TN |
1TL |
2TL |
|
Bộ 10 đề thi học kì 2 Toán lớp 7 Cánh diều có đáp án năm 2023 – 2024 – Đề 2
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2 – Cánh diều
Năm học 2023 – 2024
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 2)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Bảng sau cho biết số con của 30 gia đình trong khu dân cư:
|
Số con |
0 |
1 |
2 |
3 |
|
Số gia đình |
5 |
8 |
15 |
5 |
Điểm không hợp lí trong bảng thống kê trên là
A. Số con trong một gia đình;
B. Số gia đình trong khu dân cư;
C. Tổng số con trong gia đình;
D. Tổng số gia đình được lấy dữ liệu.
Câu 2. Biểu đồ sau cho biết Tổng sản phẩm Quốc nội (GDP) Việt Nam qua các năm:
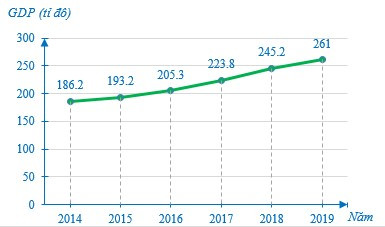
Biết đóng góp của khu vực kinh tế Công nghiệp và xây dựng vào GDP Việt Nam năm 2019 là 50%. Theo em, khu vực kinh tế này đóng góp bao nhiêu tỉ đô la?
A. 130,5 tỉ đô la;
B. 132,5 tỉ đô la;
C. 134,5 tỉ đô la;
D. 136,5 tỉ đô la.
Câu 3. Gieo hai con xúc xắc và thấy cả hai con xúc xắc đều xuất hiện mặt có số chấm là số chẵn. Trong các biến cố sau, biến cố nào là biến cố chắc chắn?
A. A: “Tổng số chấm trên cả hai con xúc xắc là một số chia 3 dư 1”;
B. B: “Tổng số chấm trên cả hai con xúc xắc là một số chia hết cho 5”;
C. C: “Tổng số chấm trên cả hai con xúc xắc là số chẵn”;
D. D: “Tổng số chấm trên cả hai con xúc xắc là một số lẻ”.
Câu 4. Trong một hộp chứa 15 quả bóng có kích thước và trọng lượng như nhau được đánh số từ 1 đến 15. Lấy ngẫu nhiên 1 quả bóng từ trong hộp. Cho biến cố F: “Lấy được quả bóng đánh số chia hết cho 9”. Xác suất của biến cố F là
A. ;
B. ;
C. ;
D. .
Câu 5. Biểu thức x3 + 8 được phát biểu bằng lời là
A. Tổng của x lập phương và 8;
B. Lập phương của tổng x và 8;
C. Ba lần tổng của x và 8;
D. Tổng của ba lần x và 8.
Câu 6. Giá trị của biểu thức: xy(x + y) + (x – y)2 tại x = – 4 và y = 2 là
A. 52;
B. 20;
C. – 20;
D. – 52.
Câu 7. Hệ số cao nhất của đa thức N(x) = –x4 + 3x + 5 là:
A. –1;
B. 1;
C. 3;
D. 5.
Câu 8. Trong các số sau, số nào là nghiệm của đa thức A(x) = x2 – 4?
A. –4;
B. 4;
C. 2;
D. 16.
Câu 9. Cho tam giác ABC có và , .
Số đo x là bao nhiêu và tam giác ABC là tam giác gì?
A. x = 30° và tam giác ABC là tam giác cân
B. x = 40° và tam giác ABC là tam giác nhọn;
C. x = 80° và tam giác ABC là tam giác tù;
D. x = 90 và tam giác ABC là tam giác vuông.
Câu 10. Cho tam giác ABC có AB < AC. Khẳng định nào dưới đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 11. Chọn câu sai?
A. Tam giác vuông có hai cạnh góc vuông bằng nhau được gọi là tam giác vuông cân;
B. Tam giác đều có ba góc bằng nhau và bằng 60°;
C. Hai góc nhọn của tam giác vuông cân bằng nhau và bằng 60°;
D. Một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
Câu 12. Nhận xét nào dưới đây sai?
A. Ba đường phân giác của một tam giác cùng đi qua một điểm;
B. Giao điểm ba đường phân giác của một tam giác cách đều ba đỉnh của tam giác đó;
C. Mỗi tam giác có ba đường phân giác;
D. Trong tam giác ABC, tia phân giác của góc A cắt BC tại D. Khi đó AD được gọi là đường phân giác của tam giác ABC.
PHẦN II. TỰ LUẬN (7,0 điểm)
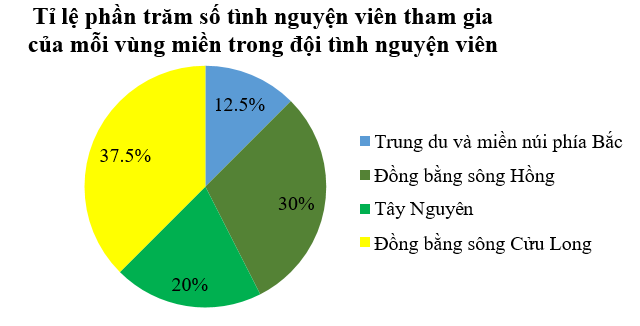
Bài 1. (1,5 điểm) Một đội tình nguyện viên tham gia chống dịch Covid – 19 gồm 40 thành viên đến từ các vùng miền được thống kê trong bảng sau:
|
Vùng miền |
Trung du và miền núi phía Bắc |
Đồng bằng sông Hồng |
Tây Nguyên |
Đồng bằng sông Cửu Long |
|
Số tình nguyện viên tham gia |
5 |
12 |
8 |
15 |
a) Lập bảng thống kê tỉ lệ phần trăm số tình nguyện viên tham gia của mỗi vùng miền trong đội tình nguyện viên đó.
b) Vẽ biểu đồ biểu diễn tỉ lệ phần trăm đã tính ở câu a.
c) Chọn ngẫu nhiên một thành viên của đội. Tính xác suất của mỗi biến cố sau:
A: “Thành viên được chọn đến từ vùng Tây Nguyên hoặc Đồng bằng sông Hồng”.
B: “Thành viên được chọn không đến từ vùng Đồng bằng sông Cửu Long”.
Bài 2. (2,0 điểm) Cho đa thức A(x) = – 11x5 + 4x3 + 12x2 + 11x5 – 13x2 + 7x + 2.
a) Thu gọn và sắp xếp đa thức A(x) theo số mũ giảm dần của biến.
b) Xác định bậc và hệ số cao nhất của đa thức A(x).
c) Tìm đa thức M(x) sao cho M(x) = A(x) – B(x) biết B(x) = –10 + 2x3 + 3x.
d) Tính M(–1) + M(0).
Bài 3. (3,0 điểm) Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AC, điểm E trên cạnh AC sao cho BD = CE.
a) Chứng minh rằng: AD = AE và DABE = DACD.
b) Chứng minh rằng: AI là đường phân giác của góc BAC.
c) Tìm vị trí của hai điểm D và E sao cho BD = DE = EC. Khi đó tìm vị trí của điểm I.
Bài 4. (0,5 điểm) Tìm giá trị nguyên của x để đa thức 4x3 – 4x2 – x + 4 chia hết cho đa thức 2x + 1.
ĐÁP ÁN ĐỀ SỐ 2
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
D |
A |
C |
A |
A |
A |
A |
C |
B |
C |
C |
B |
Hướng dẫn giải phần trắc nghiệm
Câu 1.
Đáp án đúng là: D
Theo bảng thống kê ta có tổng số gia đình trong bảng thống kê là: 5 + 8 + 15 + 5 = 33 (gia đình).
Điều này mâu thuẫn với 30 gia đình trong khu dân cư mà đề bài đã cho.
Câu 2.
Đáp án đúng là: A
Dựa vào biểu đồ ta thấy GDP của Việt Nam năm 2019 là 261 tỉ đô la;
Mà khu vực kinh tế Công nghiệp và xây dựng vào GDP Việt Nam năm 2019 là 50%, do đó khu vực này đóng góp 261.50% = 130,5 tỉ đô la.
Câu 3.
Đáp án đúng là: C
⦁ Biến cố A là biến cố ngẫu nhiên. Chẳng hạn, nếu số chấm xuất hiện trên cả hai con xúc xắc lần lượt là 2 và 5 (tổng bằng 7, chia cho 3 dư 1) thì biến cố A xảy ra; nếu số chấm xuất hiện lần lượt là 3 và 6 (tổng bằng 9, chia hết cho 3) thì biến cố A không xảy ra.
⦁ Biến cố B là biến cố ngẫu nhiên. Chẳng hạn, nếu số chấm xuất hiện trên cả hai con xúc xắc lần lượt là 4 và 6 (tổng bằng 10, chia hết cho 5) thì biến cố B xảy ra; nếu số chấm xuất hiện lần lượt là 3 và 5 (tổng bằng 8, không chia hết cho 5) thì biến cố B không xảy ra.
⦁ Ta thấy tổng của hai số chẵn cũng là một số chẵn.
Do đó biến cố C là biến cố chắc chắn và biến cố D là biến cố không thể.
Câu 4.
Đáp án đúng là: A
Vì các quả bóng đều có kích thước và trọng lượng như nhau nên các quả bóng đều có cùng khả năng được chọn.
Trong các số từ 1 đến 15, chỉ có số 9 chia hết cho chính nó.
Do đó xác suất của biến cố F là .
Câu 5.
Đáp án đúng là: A
Biểu thức x3 + 8 được phát biểu bằng lời là tổng của x lập phương và 8.
Câu 6.
Đáp án đúng là: A
Thay x = – 4 và y = 2 vào biểu thức xy(x + y) + (x – y)2, ta được:
(– 4).2(– 4 + 2) + (– 4 – 2)2 = – 8.(–2) + (–6)2 = 16 + 36 = 52.
Câu 7.
Đáp án đúng là: A
Hệ số cao nhất của đa thức N(x) = –x4 + 3x + 5 là –1.
Câu 8.
Đáp án đúng là: C
Thay lần lượt các giá trị x = –4; x = 4; x = 2; x = 16 vào đa thức A(x) ta được:
A(–4) = (–4)2 – 4 = 12 ≠ 0.
A(4) = 42 – 4 = 12 ≠ 0.
A(2) = 22 – 4 = 0
A(16) = 162 – 4 = 252 ≠ 0.
Vậy số 2 là nghiệm của đa thức A(x).
Câu 9.
Đáp án đúng là: B
Xét DABC có: 60° + x + 2x =180° (tổng ba góc trong một tam giác)
Suy ra 3x = 180° – 60° = 120°
Do đó x = 120° : 3 = 40°
Khi đó .
Ta có: 40° < 60° < 80° < 90°.
Nên ba góc của tam giác ABC đều là góc nhọn.
Do đó tam giác ABC là tam giác nhọn.
Câu 10.
Đáp án đúng là: C
Trong DABC có: AB < AC suy ra .
Câu 11.
Đáp án đúng là: C
Trong tam giác vuông tổng hai góc nhọn là 90°. Mà trong tam giác vuông cân hai góc nhọn bằng nhau nên số đo mỗi góc nhọn là 90° : 2 = 45°.
Vậy hai góc nhọn của tam giác vuông cân bằng nhau và bằng 60° là sai.
Câu 12.
Đáp án đúng là: B
Giao điểm ba đường phân giác của một tam giác cách đều ba đỉnh của tam giác đó là sai. Vì giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.
PHẦN II. TỰ LUẬN (7,0 điểm)
Hướng dẫn giải phần tự luận
Bài 1. (1,5 điểm)
a) Bảng tỉ lệ phần trăm số tình nguyện viên tham gia của mỗi vùng miền trong đội tình nguyện viên đó:
|
Vùng miền |
Trung du và miền núi phía Bắc |
Đồng bằng sông Hồng |
Tây Nguyên |
Đồng bằng sông Cửu Long |
|
Tỉ lệ phần trăm |
12,5% |
30% |
20% |
37,5% |
b) Biểu diễn tỉ lệ phần trăm số tình nguyện viên tham gia của mỗi vùng miền trong đội tình nguyện viên đó trên biểu đồ hình quạt tròn như sau:
c) Số kết quả thuận lợi cho biến cố A: “Thành viên được chọn đến từ vùng Tây Nguyên hoặc Đồng bằng sông Hồng” là: 12 + 8 = 20.
Xác suất của biến cố A là .
Số kết quả thuận lợi cho biến cố B: “Thành viên được chọn không đến từ vùng Đồng bằng sông Cửu Long” là: 40 – 15 = 25.
Xác suất của biến cố B là .
Bài 2. (2,0 điểm)
a) A(x) = – 11x5 + 4x3 + 12x2 + 11x5 – 13x2 + 7x + 2.
= (–11x5 + 11x5) + 4x3 + (12x2 – 13x2) – 7x + 2.
= 4x3 – x2 + 7x + 2.
Vậy A(x) = 4x3 – x2 + 7x + 2.
b) Đa thức A(x) có bậc là 3 và hệ số cao nhất là 4.
c) M(x) = A(x) – B(x)
M(x) = 4x3 – x2 + 7x + 2 – (–10 + 2x3 + 3x)
= 4x3 – x2 + 7x + 2 + 10 – 2x3 – 3x
= 2x3 – x2 + 4x + 12.
d) M(–1) = 2.(–1)3 – (–1)2 + 4.(–1) + 12 = 5.
M(0) = 2.03 – 02 + 4.0 + 12 = 12.
Vậy M(–1) + M(0) = 5 + 12 = 17.
Bài 3. (3,0 điểm)
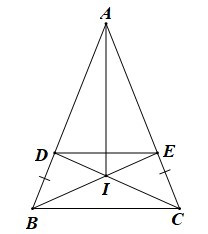
a) Ta có AB = AC (do DABC cân tại A) và BD = CE (giả thiết)
Suy ra AB – BD = AC – CE hay AD = AE.
Xét DABE và DACD có:
AB = AC (chứng minh trên);
là góc chung;
AD = AE (chứng minh trên)
Do đó DABE = DACD (c.g.c).
b) Từ DABE = DACD suy ra (hai góc tương ứng)
Mà (do DABC cân tại A)
Suy ra
Tam giác IBC có nên là tam giác cân tại I.
Do đó IB = IC.
Xét DABI và DACI có:
AB = AC (chứng minh trên);
AI là cạnh chung;
IB = IC (chứng minh trên).
Do đó DABI = DACI (c.c.c)
Suy ra (hai góc tương ứng).
Nên AI là tia phân giác của góc BAC.
c) Xét DADE có AD = AE nên DADE cân tại A.
Suy ra .
Mà (tổng ba góc trong một tam giác)
Suy ra .
Tương tự với tam giác ABC cân tại A ta có
Từ (1) và (2) suy ra
Mà hai góc này ở vị trí đồng vị nên DE // BC.
Suy ra (hai góc so le trong) (3)
Do BD = DE nên DBDE là tam giác cân tại D
Suy ra (4)
Từ (3) và (4) suy ra
Khi đó BE là đường phân giác của góc ABC.
Tương tự, với DE = EC ta cũng chứng minh được CD là đường phân giác của góc ACB.
Xét tam giác ABC có BE, CE là hai đường phân giác của tam giác cắt nhau tại I
Suy ra I cách đều ba cạnh của tam giác ABC.
Vậy để BD = DE = EC thì BE và CD là hai đường phân giác của DABC, khi đó I cách đều ba cạnh của DABC.
Bài 4. (0,5 điểm)
Thực hiện phép chia đa thức như sau:
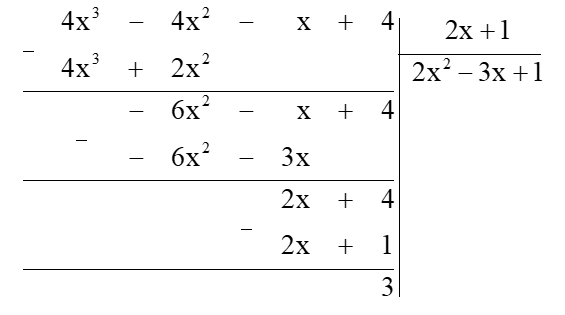
Do đó phép chia trên có thương là 2x2 – 3x + 1 và dư 3.
Để phép chia là phép chia hết thì 3 ⋮ (2x + 1), hay 2x + 1 ∈ Ư(3) = {1; –1; 3; –3}.
Ta có bảng sau:
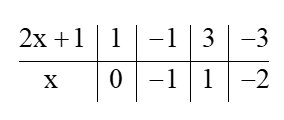
Vậy x ∈ {–2; –1; 0; 1}.
Bộ 10 đề thi học kì 2 Toán lớp 7 Cánh diều có đáp án năm 2023 – 2024 – Đề 3
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2 – Cánh diều
Năm học 2023 – 2024
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 3)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Cho các dãy dữ liệu:
(1) Tên của mỗi bạn học sinh trong lớp 7A.
(2) Số lượng học sinh của các lớp 7 đạt điểm 10 thi giữa học kì I.
(3) Số nhà của mỗi bạn học sinh lớp 7B.
(4) Số lượng nhóm nhạc yêu thích của mỗi bạn học sinh trong lớp.
Trong các dãy dữ liệu trên, dãy dữ không phải là số là
A. (1);
B. (2);
C. (3);
D. (4).
Câu 2. Biểu đồ dưới đây cho biết tỉ lệ các loại kem bán được trong một ngày của một cửa hàng kem.
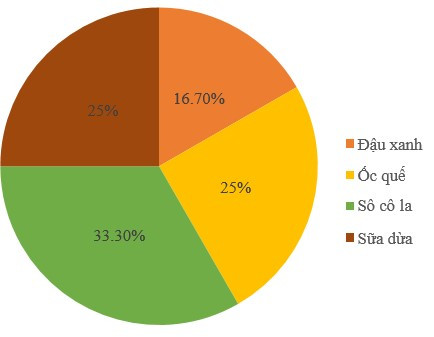
Biết rằng một ngày cửa hàng đó bán được 100 cái kem. Số lượng kem ốc quế bán được trong một ngày là bao nhiêu?
A. 20 cái;
B. 25 cái;
C. 30 cái;
D. 35 cái.
Câu 3. Tung hai con xúc xắc màu xanh và đỏ rồi quan sát số chấm xuất hiện trên mặt hai con xúc xắc. Xét biến cố A: “Số chấm trên mặt hai con xúc xắc bằng nhau”. Khẳng định nào sau đây là đúng?
A. Biến cố A là biến cố không thể;
B. Biến cố A là biến cố chắc chắn;
C. Biến cố A là biến cố ngẫu nhiên;
D. Cả A, B, C đều đúng.
Câu 4. Một chiếc bình thủy tinh đựng 1 ngôi sao giấy màu tím, 1 ngôi sao giấy màu xanh, 1 ngôi sao giấy màu vàng, 1 ngôi sao giấy màu đỏ. Các ngôi sao có kích thước và khối lượng như nhau. Lấy ngẫu nhiên 1 ngôi sao từ trong bình. Cho biến cố Y: “Lấy được 1 ngôi sao màu tím hoặc màu đỏ”. Xác suất của biến cố Y là
A. ;
B. ;
C. ;
D. 1.
Câu 5. Một người đi bộ trong x (giờ) với vận tốc 4 (km/h) và sau đó đi bằng xe đạp trong y (giờ) với vận tốc 18 (km/h). Biểu thức đại số biểu thị tổng quãng đường đi được của người đó là
A. 4(x + y);
B. 22(x + y);
C. 4y + 18x;
D. 4x + 18y.
Câu 6. Giá trị của biểu thức A = –(2a + b) tại a = 1; b = 3 là
A. A = 5;
B. A = –5;
C. A = 1;
D. A = –1.
Câu 7. Hệ số tự do của đa thức 10 – 9x2 – 7x5 + x6 – x4 là
A. –1;
B. –7;
C. 1;
D. 10.
Câu 8. Cho đa thức A(t) = 2t2 – 3t + 1. Phần tử nào trong tập hợp {‒1; 0; 1; 2} là nghiệm của A(t)?
A. ‒1;
B. 0;
C. 1;
D. 2.
Câu 9. Trong một tam giác, đối diện với cạnh nhỏ nhất là một
A. góc nhọn;
B. góc vuông;
C. góc tù;
D. góc bẹt.
Câu 10. Cho tam giác ABC có , . Số đo góc C là:
A.70°;
B. 80°;
C. 90°;
D. 100°.
Câu 11. Bộ ba số đo nào dưới đây có thể là độ dài ba cạnh của một tam giác?
A. 7 cm, 3 cm, 4 cm;
B. 7 cm, 3 cm, 5 cm;
C. 7 cm, 3 cm, 2 cm;
D. 7 cm, 3 cm, 3 cm.
Câu 12. Trong một tam giác, trực tâm là giao điểm của ba đường nào?
A. Đường phân giác;
B. Đường trung tuyến;
C. Đường trung trực;
D. Đường cao.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
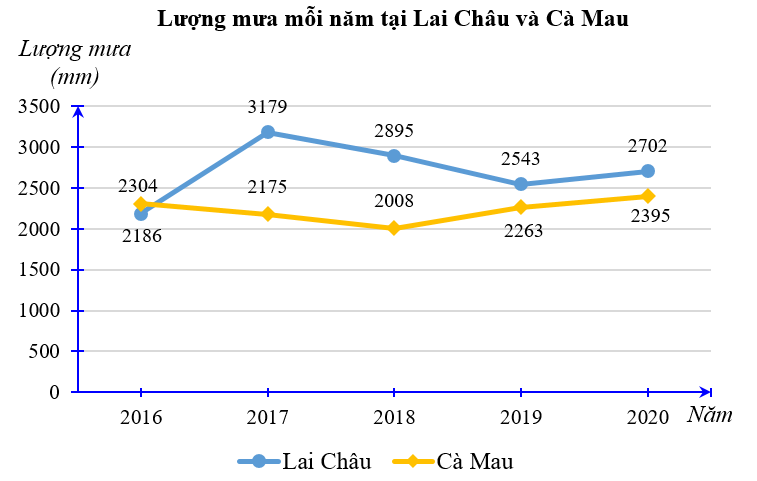
(Nguồn: Tổng cục Thống kê)
a) Tính tổng lượng mưa tại mỗi tỉnh Lai Châu và Cà Mau trong giai đoạn 2016 – 2020.
b) Năm 2017, lượng mưa tại Cà Mau bằng bao nhiêu phần trăm lượng mưa tại Lai Châu (làm tròn kết quả với độ chính xác 0,005)?
c) Chọn ngẫu nhiên 1 năm trong 5 năm đó. Tính xác suất của các biến cố sau:
A: “Tại năm được chọn, lượng mưa ở Cà Mau cao hơn ở Lai Châu”;
B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m”;
Bài 2. (2,0 điểm) Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
a) Tìm đa thức A(x).
b) Xác định bậc và hệ số cao nhất của đa thức A(x).
c) Tìm đa thức M(x) sao cho M(x) = A(x).B(x) biết B(x) = –x2 + x.
d) Tính M(‒1), từ đó kết luận số ‒1 có phải là nghiệm của đa thức M(x) hay không.
Bài 3. (3,0 điểm) Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
a) DABD = DEBD từ đó suy ra AD = ED.
b) BD là đường trung trực của đoạn thẳng AE và AD < DC.
c) Ba điểm E, D, F thẳng hàng.
Bài 4. (0,5 điểm) Xác định các hằng số a và b sao cho đa thức x4 + ax2 + b chia hết cho đa thức x2 – x + 1.
ĐÁP ÁN ĐỀ SỐ 3
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Bảng đáp án:
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
A |
B |
C |
B |
D |
A |
D |
C |
A |
D |
B |
D |
Hướng dẫn giải phần trắc nghiệm
Câu 1.
Đáp án đúng là: A
Tên của mỗi bạn học sinh trong lớp 7A là dãy dữ liệu không phải là số.
Câu 2.
Đáp án đúng là: B
Số lượng kem ốc quế bán được trong một ngày là: cái.
Câu 3.
Đáp án đúng là: C
Khi tung hai con xúc xắc màu xanh và đỏ thì số chấm xuất hiện trên mặt hai con xúc xắc có thể bằng nhau, chẳng hạn hai con xúc xắc đều xuất hiện 1 chấm; số chấm xuất hiến trên mặt hai con xúc xắc có thể không bằng nhau, chẳng hạn con xúc xắc xanh xuất hiện mặt 1 chấm, con xúc xắc đỏ xuất hiện mặt 2 chấm.
Vậy biến cố A: “Số chấm trên mặt hai con xúc xắc bằng nhau” là biến cố ngẫu nhiên.
Câu 4.
Đáp án đúng là: B
Trong bình có tất cả 4 ngôi sao có màu khác nhau: màu tím, màu xanh, màu vàng và màu đỏ.
Do các ngôi sao có cùng kích thước và khối lượng như nhau nên các ngôi sao đều có cùng khả năng được chọn.
Vì trong bình có 1 ngôi sao màu tím và 1 ngôi sao màu đỏ nên có 2 kết quả làm cho biến cố Y: “Lấy được 1 ngôi sao màu tím hoặc màu đỏ” xảy ra.
Do đó xác suất của biến cố Y là
Câu 5.
Đáp án đúng là: D
Quãng đường mà người đó đi bộ là : 4.x = 4x (km)
Quãng đường mà người đó đi bằng xe đạp là: 18.y = 18y (km)
Tổng quãng đường đi được của người đó là: 4x + 18y (km).
Câu 6.
Đáp án đúng là: A
Thay a = 1, b = 3 vào biểu thức A ta được:
A = –(2.1 + 3) = –(2 + 3) = –5.
Câu 7.
Đáp án đúng là: D
Sắp xếp đa thức đã cho theo lũy thừa giảm dần của biến y như sau:
10 – 9x2 – 7x5 + x6 – x4
= x6 – 7x5 – x4 – 9x2 + 10
Hệ số tự do của đa thức đã cho là 10.
Câu 8.
Đáp án đúng là: C
Xét đa thức A(t) = 2t2 – 3t + 1, ta có:
A(‒1) = 2.(‒1)2 – 3.(‒1) + 1 = 2 + 3 + 1 = 6 ≠ 0.
A(0) = 2.02 – 3.0 + 1 = 0 + 0 + 1 = 1 ≠ 0.
A(1) = 2.12 – 3.1 + 1 = 2 ‒ 3 + 1 = 0.
A(2) = 2.22 – 3.2 + 1 = 8 ‒ 6 + 1 = 3 ≠ 0.
Vậy số 1 là là một nghiệm của A(t).
Câu 9.
Đáp án đúng là: A
Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhỏ nhất, mà góc nhỏ nhất của một tam giác là góc nhọn.
Câu 10.
Đáp án đúng là: D
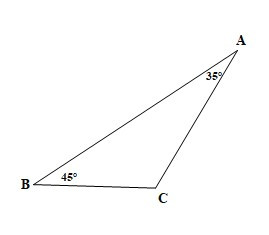
Xét DABC có: ( định lí tổng ba góc trong một tam giác)
Suy ra .
Câu 11.
Đáp án đúng là: B
Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
Ta thấy:
3 + 4 = 7 nên bộ ba số đo 7 cm, 3 cm, 4 cm không thể là ba cạnh của một tam giác.
3 + 5 > 7 nên bộ ba số đo 7 cm, 3 cm, 5 cm có thể là ba cạnh của một tam giác.
2 + 3 < 7 nên bộ ba số đo 7 cm, 3 cm, 2 cm không thể là ba cạnh của một tam giác.
3 + 3 < 7 nên bộ ba số đo 7 cm, 3 cm, 4 cm không thể là ba cạnh của một tam giác.
Câu 12.
Đáp án đúng là: D
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
PHẦN II. TỰ LUẬN (7,0 điểm)
Hướng dẫn giải phần tự luận
Bài 1. (1,5 điểm)
a) Tổng lượng mưa tại mỗi tỉnh Lai Châu trong giai đoạn 2016 – 2020 là:
2 186 + 3 179 + 2 895 + 2 543 + 2 702 = 13 505 (mm).
Tổng lượng mưa tại mỗi tỉnh Cà Mau trong giai đoạn 2016 – 2020 là:
2 304 + 2 175 + 2 008 + 2 263 + 2 395 = 11 145 (mm).
b) Năm 2017, lượng mưa tại Cà Mau và Lai Châu lần lượt là 2 175 mm và 3 179 mm.
Trong năm 2017, lượng mưa tại Cà Mau bằng số phần trăm lượng mưa tại Lai Châu là: .
c) • Quan sát biểu đồ trên thấy có 1 năm mà lượng mưa ở Cà Mau cao hơn lượng mưa ở Lai Châu là: năm 2016.
Vì chọn ngẫu nhiên một năm nên xác suất của biến cố A: “Tại năm được chọn lượng mưa ở Cà Mau cao hơn ở Lai Châu” là P(A) =
• Ta có: 25 m = 25 000 mm.
Quan sát biểu đồ ta thấy tất cả các năm 2016, 2017, 2018, 2019, 2020 đều có lượng mưa ở Cà Mau thấp hơn 25 000 mm.
Do đó biến cố B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m” là biến cố chắc chắn nên P(B) = 1.
Vậy P(A) = , P(B) = 1.
Bài 2. (2,0 điểm)
a) Ta có A(x) = –9x3 – 8x2 + 5x + 11 + (9x3 + 8x2 – 2x – 7)
A(x) = –9x3 – 8x2 + 5x + 11 + 9x3 + 8x2 – 2x – 7
A(x) = 3x + 4
b) Đa thức A(x) có bậc là 1 và hệ số cao nhất là 3.
c) M(x) = A(x).B(x)
M(x) = (3x + 4).(–x2 + x)
= 3x.(–x2 + x) + 4(–x2 + x)
= –3x3 + 3x2 – 4x2 + 4x
= –3x3 – x2 + 4x.
d) M(‒1) = –3.(‒1)3 – (‒1)2 + 4.(‒1) = 3 – 1 – 4 = ‒2 ≠ 0.
Vậy số ‒1 không là nghiệm của đa thức M(x).
Bài 3. (3,0 điểm)
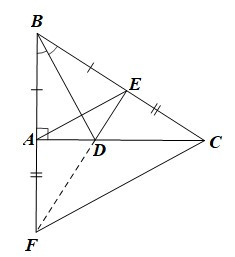
a) Xét DABD và DEBD có:
BA = BE (giả thiết);
(do BD là tia phân giác của góc ABC);
BD là cạnh chung.
Do đó DABD = DEBD (c.g.c)
Suy ra AD = ED (hai cạnh tương ứng).
b) • Do BA = BE nên B nằm trên đường trung trực của AE.
Do AD = ED nên D nằm trên đường trung trực của AE.
Suy ra BD là đường trung trực của AE.
• Do DABD = DEBD nên (hai góc tương ứng)
Xét DDCE vuông tại E có DC là cạnh huyền nên DC là cạnh lớn nhất.
Do đó DC > DE.
Mà AD = DE nên AD < DC.
c) • Tam giác BAE có BA = BE nên cân tại B.
Do đó .
Mà .
Suy ra
Tương tự với tam giác BFC ta cũng có
Từ (1) và (2) suy ra .
Mà hai góc này ở vị trí đồng vị nên AE // FC.
Lại có AE ⊥ BD (do BD là đường trung trực của AE)
Do đó BD ⊥ FC.
• Xét DBFC có BD ⊥ FC, CA ⊥ BF, BD cắt CA tại D nên D là trực tâm của DBFC.
Suy ra FD ⊥ BC.
Mà DE ⊥ BC (do )
Do đó ba điểm F, D, E thẳng hàng.
Bài 4. (0,5 điểm)
Ta thực hiện phép chia đa thức như sau:
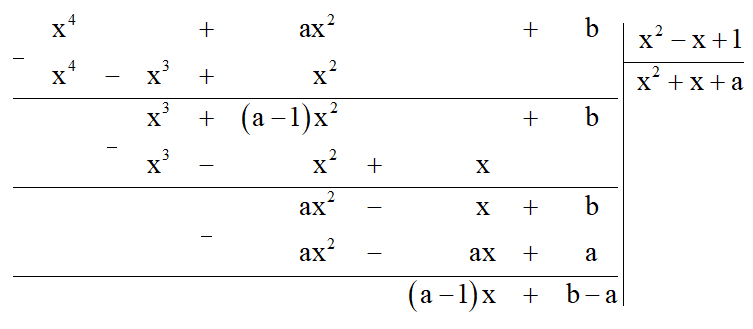
Ta được thương của phép chia trên là x2 + x + a, dư (a – 1)x + b – a.
Để đa thức x4 + ax2 + b chia hết cho đa thức x2 – x + 1 thì dư phải bằng 0 với mọi x.
Do đó (a – 1)x + b – a = 0 với mọi x.
Suy ra , tức là .
Vậy a = b = 1.
Bộ 10 đề thi học kì 2 Toán lớp 7 Cánh diều có đáp án năm 2023 – 2024 – Đề 4
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2 – Cánh diều
Năm học 2023 – 2024
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 4)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Dựa vào bảng thống kê học lực của học sinh lớp 7A được cho bên dưới.
|
Học lực |
Yếu |
Trung bình |
Khá |
Giỏi |
|
Số học sinh |
4 |
6 |
20 |
5 |
Hãy phân loại dữ liệu trong bảng thống kê dựa trên tiêu chí định tính và định lượng:
A. Học lực (yếu, trung bình, khá, giỏi) là dữ liệu định lượng; số học sinh là dữ liệu định tính;
B. Học lực (yếu, trung bình, khá, giỏi) là dữ liệu định tính; số học sinh là dữ liệu định lượng;
C. Cả học lực (yếu, trung bình, khá, giỏi) và số học sinh đều là dữ liệu định tính;
D. Cả học lực (yếu, trung bình, khá, giỏi) và số học sinh đều là dữ liệu định lượng.
Câu 2. Cho biểu đồ sau:
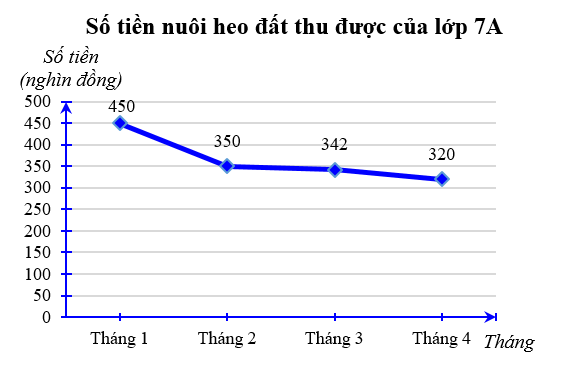
Tổng số tiền heo đất thu được trong 4 tháng là bao nhiêu?
A. 1 562 000 đồng;
B. 1 462 000 đồng;
C. 1 362 000 đồng;
D. 1 262 000 đồng.
Câu 3. Xác suất để ngày mao trời mưa là 30%, trời không mưa và nhiều mây là 45%, trời không mưa và ít mây là 25%. Biến cố nào sau đây dễ xảy ra nhất?
A. Ngày mai trời mưa;
B. Ngày mai trời không mưa và nhiều mây;
C. Ngày mai trời không mưa và ít mây;
D. Ngày mai trời không mưa và không có mây.
Câu 4. Trong một chiếc hộp có 4 chiếc thẻ được ghi số 2; 4; 5; 7. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Xét các biến cố sau:
A: “Rút được thẻ ghi số nguyên tố”;
B: “Rút được thẻ ghi số nhỏ hơn 8”;
C: “Rút được thẻ ghi số lớn hơn 9”.
Biến cố ngẫu nhiên là
A. Biến cố A;
B. Biến cố B;
C. Biến cố C;
D. Cả ba biến cố A, B, C.
Câu 5. Giả sử độ dài cạnh một hình vuông là (x + 1) (cm). Đa thức biểu thị diện tích của hình vuông đó là
A. x2 + 1;
B. x2 + 2x + 1;
C. x2 + x + 1;
D. 2x + 2.
Câu 6. Giá trị của biểu thức P = 3x3 – 2y2 – 2xy tại x = ‒2 và y = ‒3 là
A. ‒54;
B. ‒24;
C. ‒18;
D. 36.
Câu 7. Hệ số cao nhất của đa thức A(x) = –5x2(2x3 + x – 4) là
A. –10;
B. –5;
C. –20;
D. 20.
Câu 8. Giá trị của x thỏa mãn 4x2 – 4x(x – 2) = 24 là
A. x = 2;
B. x = 4;
C. x = 1;
D. x = 3.
Câu 9. Cho tam giác ABC có AB = 3 cm; BC = 4 cm; AC = 5 cm. Khi đó:
A. Góc A lớn hơn góc B;
B. Góc B nhỏ hơn góc C;
C. Góc A nhỏ hơn góc C;
D. Góc B là góc lớn nhất.
Câu 10. Cho tam giác ABC có AB = 7 cm, AC = 1 cm. Độ dài cạnh BC là một số nguyên thì tam giác ABC là
A. Tam giác cân;
B. Tam giác vuông;
C. Tam giác vuông cân;
D. Tam giác tù.
Câu 11. Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Vẽ DE vuông góc với BC tại E. Câu nào dưới đây là đúng?
A. AD < DC;
B. AB > BC;
C. DE > DC;
D. AC > BC.
Câu 12. Cho tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G. Kết quả nào sau đây là sai?
A. ;
B. ;
C. ;
D. .
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
1. Biểu đồ hình quạt tròn sau biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) lực lượng lao động (từ 15 tuổi trở lên) phân theo trình độ chuyên môn kĩ thuật của nước ta năm 2020.
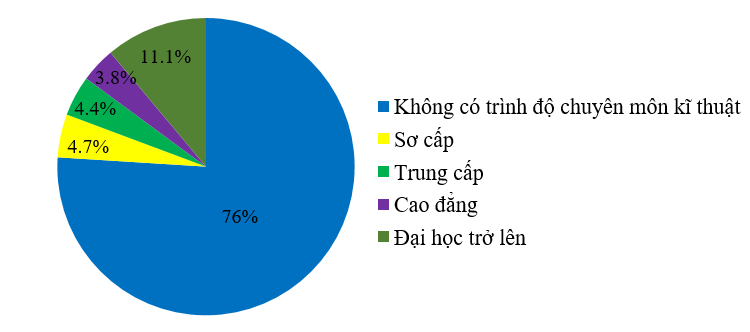
a) Trong năm 2020, lực lượng lao động không có trình độ chuyên môn kĩ thuật gấp bao nhiêu lần lực lượng lao động có trình độ đại học trở lên (làm tròn kết quả với độ chính xác 0,5)?
b) Số lao động không có trình độ chuyên môn kĩ thuật là bao nhiêu triệu người? Biết có 54,6 triệu người từ 15 tuổi trở lên thuộc lực lượng lao động của cả nước trong năm 2020 (làm tròn kết quả đến hàng phần trăm).
2. Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 49, 500; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 26”.
b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5”.
Bài 2. (2,0 điểm) Cho hai đa thức P(x) = 2x4 + 2x3 – 3x2 + x + 6;
Q(x) = x4 + x3 – x2 + 2x + 1.
a) Xác định bậc và hệ số cao nhất của đa thức P(x).
b) Tìm đa thức M(x) biết P(x) + M(x) = 2Q(x).
c) Tính N(–2) biết N(x) = (x – 1).M(x).
Bài 3. (3,0 điểm) Cho tam giác ABC có ba góc nhọn. Các điểm M, N, P lần lượt là trung điểm của cạnh BC, AB, AC. Gọi O là giao điểm các đường trung trực của tam giác ABC. Trên tia đối của tia MO lấy điểm D sao cho MO = MD. Trên tia đối của tia NO lấy điểm F sao cho NO = NF. Trên tia đối của tia PO lấy điểm E sao cho PO = PF.
a) Chứng minh DANO = DBNF, từ đó suy ra AO = BF và AO // BF.
b) Chứng minh hình lục giác AFBDCE có 6 cạnh bằng nhau và 2 trong 6 cạnh đó đôi một song song.
c) Chứng minh DABC = DDEF.
Bài 4. (0,5 điểm) Cho x2 – 4x + 1 = 0. Tính giá trị biểu thức A = x5 – 3x4 – 3x3 + 6x2 – 20x + 2030.
Bộ 10 đề thi học kì 2 Toán lớp 7 Cánh diều có đáp án năm 2023 – 2024 – Đề 5
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2 – Cánh diều
Năm học 2023 – 2024
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 5)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Kết quả tìm hiểu về sở thích môn Toán của 5 bạn học sinh trường THCS A được cho trong bảng thống kê sau:
|
STT |
Tuổi |
Giới tính |
Sở thích |
| 1 | 12 |
Nữ |
Thích |
| 2 | 13 |
Nam |
Không thích |
| 3 | 14 |
Nam |
Thích |
| 4 | 14 |
Nữ |
Rất thích |
| 5 | 12 |
Nữ |
Không thích |
Phát biểu nào sau đây là đúng?
A. Dữ liệu số tuổi là dữ liệu định tính;
B. Dữ liệu số tuổi là dữ liệu định lượng;
C. Dữ liệu giới tính là dữ liệu định lượng;
D. Dữ liệu sở thích là dữ liệu định lượng.
Câu 2. Biểu đồ hình quạt dưới đây trên thể hiện diện tích đất trồng: hoa huệ, hoa hồng và hoa loa kèn trong vườn hoa nhà bạn My.
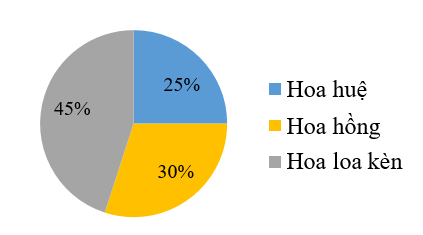
Biết diện tích đất trồng hoa là 10 m2. Diện tích đất trồng hoa hồng là
A. 10 m2;
B. 100 m2;
C. 4,5 m2;
D. 45 m2.
Câu 3. Tung đồng thời một con xúc xắc và một đồng xu. Biến cố nào sau đây là biến cố không thể?
A. Đồng xu xuất hiện mặt sấp;
B. Đồng xu xuất hiện mặt ngửa và số chấm xuất hiện trên con xúc xắc nhỏ hơn 1;
C. Xúc xắc xuất hiện mặt 6 chấm;
D. Đồng xu xuất hiện mặt ngửa và số chấm xuất hiện trên con xúc xắc là số chẵn.
Câu 4. Có hai chiếc hộp, mỗi chiếc hộp đựng 4 tấm thẻ ghi các số 1; 2; 3; 4. Rút ngẫu nhiên một tấm thẻ từ mỗi hộp.
Biến cố “Tổng số ghi trên hai tấm thẻ lớn hơn 1” là
A. Biến cố chắc chắn;
B. Biến cố không thể;
C. Biến cố ngẫu nhiên;
D. Cả A, B, C đều đúng.
Câu 5. Biểu thức biểu thị “Tích của tổng x và y với hiệu của x và y” là
A. x + y.x – y;
B. (x + y).x – y;
C. (x + y).(x – y);
D. x.y.(x + y).(x – y).
Câu 6. Giá trị của biểu thức x2 – y tại x = ‒2; y = ‒1 là
A. 5;
B. ‒3;
C. 3;
D. ‒5.
Câu 7. Bậc của đa thức M(x) = 2x3 + 3x – 2x3 + 1 là
A. 1;
B. 2;
C. 3;
D. 4.
Câu 8. Số nghiệm của đa thức x(x2 + 1) là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 9. Kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng sau có độ dài là ba cạnh của một tam giác:
A. 3 cm; 5 cm; 8 cm;
B. 4 cm; 5 cm; 9 cm;
C. 2 cm; 5 cm; 7 cm;
D. 2 cm; 5 cm; 6 cm.
Câu 10. Cho tam giác ABC có AM là đường trung tuyến và G là trọng tâm tam giác. Biết AG = x + 2 và AM = x + 4. Giá trị của x là
A. 1;
B. 2;
C. 3;
D. 4.
Câu 11. Cho DDEF vuông tại E có . Khẳng định nào sau đây đúng?
A. ;
B. DE > DF > EF;
C. DE > EF > DF;
D. DF > DE > EF.
Câu 12. Trong một tam giác, tâm đường tròn nột tiếp tam giác là
A. giao điểm của ba đường trung tuyến;
B. giao điểm của ba đường trung trực;
C. giao điểm của ba đường phân giác;
D. giao điểm của ba đường trung trực.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Lượng điện tiêu thụ mỗi ngày trong 7 ngày đầu tháng 02/2022 của một hộ gia đình được cho ở biểu đồ sau:
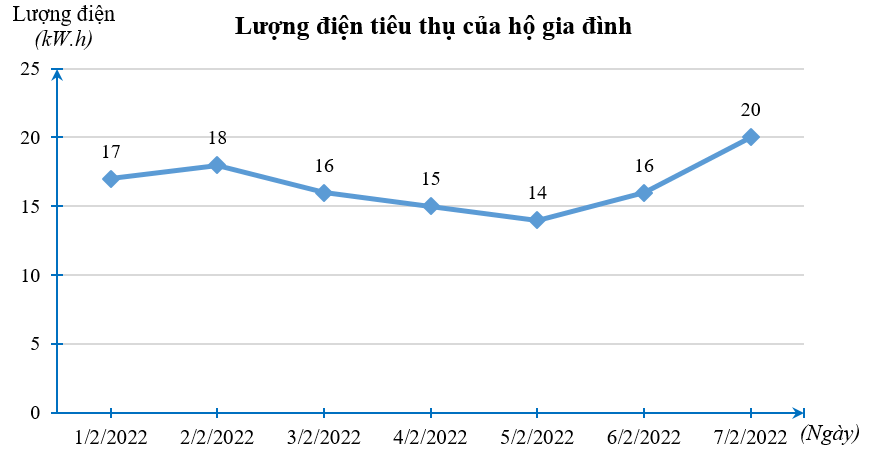
a) Ngày nào trong tuần đầu tiên của tháng 02/2022, hộ gia đình tiêu thụ lượng điện ít nhất? Nhiều nhất?
b) Trong tuần đầu tiên của tháng 02/2022, hộ gia đình đó tiêu thụ hết bao nhiêu kW.h điện? Trung bình mỗi ngày tiêu thụ bao nhiêu?
c) Chọn ngẫu nhiên 1 ngày trong 7 ngày đó. Tính xác suất của mỗi biến cố sau:
A: “Chọn được ngày hộ gia đình sử dụng 16 kW.h điện trong ngày”;
B: “Chọn được ngày hộ gia đình sử dụng dưới 20 kW.h điện trong ngày”.
Bài 2. (2,0 điểm) Cho đa thức A(x) = x2 + 3x – 9 và B(x) = x2 – 2x + 1.
a) Tính M(x) = A(x) + B(x) và N(x) = A(x) – B(x).
b) Xác định bậc và hệ số cao nhất của đa thức M(x), N(x).
c) Tính P(‒2) biết P(x) = M(x).N(x).
Bài 3. (3,0 điểm) Cho tam giác ABC cân tại A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE. Gọi M là trung điểm của BC.
a) Chứng minh rằng tam giác ADE là tam giác cân.
b) Chứng minh AM là tia phân giác của góc DAE.
c) Kẻ BH ⊥ AD và CK ⊥ AE. Chứng minh BH = CK.
d) Chứng minh ba đường thẳng AM, BH và CK đồng quy.
Bài 4. (0,5 điểm) Tìm các số nguyên a và b để đa thức A(x) = x4 – 3x3 + ax + b chia hết cho đa thức B(x) = x2 – 3x + 4.