Lý thuyết Toán lớp 7 Bài 1: Biểu thức số. Biểu thức đại số
A. Lý thuyết
I. Biểu thức số
– Các số được nối với nhau bởi dấu các phép tính (cộng, trừ, nhân, chia, nâng lên luỹ thừa) tạo thành một biểu thức số. Đặc biệt, mỗi số cũng được coi là một biểu thức số.
– Trong biểu thức số có thể có các dấu ngoặc để chỉ thứ tự thực hiện các phép tính.
– Khi thực hiện các phép tính trong một biểu thức số, ta nhận được một số. Số đó được gọi là giá trị của biểu thức số đã cho.
Ví dụ: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) 2022 không phải là biểu thức số.
b) Biểu thức số phải có đầy đủ các phép tính cộng, trừ, nhân, chia, nâng lên luỹ thừa.
Hướng dẫn giải
a) Sai. Vì một số cũng được coi là một biểu thức số nên 2022 là biểu thức số.
b) Sai. Vì trong biểu thức số không nhất thiết phải có đầy đủ các phép tính cộng, trừ, nhân, chia, nâng lên luỹ thừa.
Chẳng hạn: 22 + 1 chỉ có phép nâng lên luỹ thừa và phép cộng cũng là một biểu thức số.
Ví dụ: Viết biểu thức số biểu thị:
a) Chu vi hình chữ nhật có chiều dài là 30 cm, chiều rộng là 20 cm.
b) Diện tích của hình tròn có bán kính 40 cm.
Hướng dẫn giải:
a) Biểu thức biểu thị chu vi hình chữ nhật có chiều dài 30 cm, chiều rộng 20 cm là:
2(30 + 20) (cm).
b) Biểu thức biểu thị diện tích hình tròn có bán kính 40 cm là: p. 402 (cm2).
Ví dụ: Một trường THCS cử một đoàn giáo viên tham gia tập huấn gồm: 1 trưởng đoàn, mỗi khối 6, 7, 8, 9 đều có 2 giáo viên toán, 1 giáo viên văn. Biểu thức số nào dưới đây biểu thị tổng số thành viên của đoàn?
a) 1 + 4. 2 + 1 (thành viên);
b) 1 + 4. (2 + 1) (thành viên).
Hướng dẫn giải
Biểu thức biểu thị số thành viên của mỗi khối là: 2 + 1 (thành viên).
Biểu thức biểu thị số thành viên của 4 khối là: 4. (2 + 1) (thành viên).
Biểu thức biểu thị tổng số thành viên của đoàn là: 1 + 4. (2 + 1) (thành viên).
II. Biểu thức đại số
– Biểu thức gồm các số và các biến số (đại diện cho số) được nối với nhau bởi các kí hiệu phép toán cộng, trừ, nhân, chia, nâng lên luỹ thừa được gọi là biểu thức đại số.
– Biểu thức số cũng là biểu thức đại số.
– Trong biểu thức đại số có thể có các dấu ngoặc để chỉ thứ tự thực hiện các phép tính.
– Chú ý: Để cho gọn, khi viết các biểu thức đại số ta thường:
+ Không viết dấu nhân giữa các chữ, cũng như giữa số và chữ.
Chẳng hạn: viết xy thay cho x.y; viết 2x thay cho 2.x.
+ Viết x thay cho 1. x; viết –x thay cho (–1). x.
– Trong biểu thức đại số, vì chữ đại diện cho số nên khi thực hiện các phép tính trên các chữ, ta có thể áp dụng những tính chất, quy tắc phép tính như trên các số.
Chẳng hạn:
2x + x = 3x; 5x – 2x = 3x;
x.x2 = x3; x + y = y + x;
xy = yx; x(yz) = (xy)z;
x + (y + z) = (x + y) + z;
x(y + z) = xy + xz;
–x(y – z) = –xy + xz; …
Ví dụ: Trong các biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) 2. 3 – 3. 5 là biểu thức đại số;
b) 3x2 + 5x + 2 là biểu thức đại số;
c) 2x + 3y + z không phải là biểu thức đại số.
Hướng dẫn giải:
a) Đúng. Vì 2. 3 – 3. 5 là biểu thức số nên cũng là biểu thức đại số;
b) Đúng. Vì 3x2 + 5x + 2 được nối với nhau bởi các phép toán và x đại diện cho số nên biểu thức này là biểu thức đại số.
c) Sai. Vì 2x + 3y + z được nối với nhau bởi các phép toán và x, y, z đại diện cho các số nên biểu thức này là biểu thức đại số.
Ví dụ: Viết biểu thức biểu thị diện tích toàn phần (tổng diện tích tất cả các mặt) của hình hộp chữ nhật có ba kích thước là 4 (cm), x (cm), y (cm) như hình vẽ dưới đây:
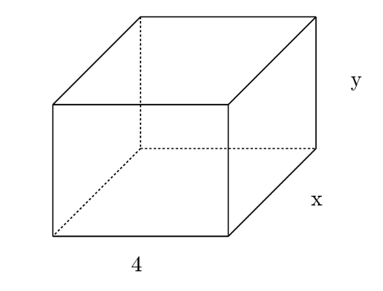
Hướng dẫn giải:
Diện tích xung quanh của hình hộp chữ nhật là:
2(4 + x). y (cm2)
Diện tích đáy của hình hộp chữ nhật là: 4x (cm2)
Diện tích toàn phần của hình hộp chữ nhật là:
2(4 + x). y + 2.4x (cm2)
Vậy biểu thức biểu thị diện tích toàn phần của hình hộp chữ nhật trên là: 2(4 + x). y + 2.4x (cm2).
III. Giá trị của biểu thức đại số
Để tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay các giá trị cho trước đó vào biểu thức rồi thực hiện các phép tính.
Ví dụ: Tính giá trị của biểu thức x2 – 5y + 1 khi x = 4 và y = 2.
Hướng dẫn giải
Thay x = 4 và y = 2 vào biểu thức trên ta được:
42 – 5.2 + 1 = 16 – 10 + 1 = 7
Vậy khi x = 4 và y = 2 thì giá trị của biểu thức x2 – 5y + 1 bằng 7.
Ví dụ: Bác Hoa mua một túi rau và một số quả cam. Biết rằng mỗi kilôgam cam có giá 40 nghìn đồng và túi rau có giá 15 nghìn đồng.
a) Hãy viết biểu thức biểu thị tổng số tiền bác Hoa phải trả nếu số cam bác Hoa mua là x kilôgam.
b) Giả sử số cam bác Hoa mua là 2,5 kilôgam. Sử dụng kết quả câu a, em hãy tính xem bác Hoa phải trả tất cả bao nhiêu tiền.
Hướng dẫn giải
a) Số tiền bác Hoa phải trả cho x kilôgam cam là 40x (nghìn đồng).
Số tiền bác Hoa phải trả cho một túi rau là 15 nghìn đồng.
Vậy biểu thức biểu thị tổng số tiền bác Hoa phải trả là:
40x + 15 (nghìn đồng)
b) Thay x = 2,5 vào biểu thức 40x + 15, ta được:
40. 2,5 + 15 = 115 (nghìn đồng)
Vậy bác Hoa phải trả tất cả là 115 nghìn đồng.
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Một quả bưởi năm roi giá 60 000 đồng, một kilôgam cam canh giá 50 000 đồng. Viết biểu thức đại số cho số tiền ứng với x quả bưởi năm roi và y kilôgam cam canh.
Hướng dẫn giải
Ta có:
x quả bưởi năm roi có giá là 60 000x (đồng).
y kilôgam cam canh có giá là 50 000y (đồng).
Biểu thức đại số cho số tiền ứng với x quả bưởi năm roi và y cân cam canh là:
60 000x + 50 000y (đồng).
Bài 2. Trong một ngày hè, buổi sáng nhiệt độ là x °C, buổi trưa tăng thêm y °C so với buổi sáng. Buổi chiều lúc mặt trời lặn nhiệt độ lại giảm đi z °C so với buổi trưa. Viết biểu thức đại số biểu thị nhiệt độ lúc mặt trời lặn vào buổi chiều theo x, y, z và tính nhiệt độ lúc mặt trời lặn khi x = 30 °C, y = 6 °C, z = 10 °C.
Hướng dẫn giải
Biểu thức đại số biểu thị nhiệt độ lúc mặt trời lặn là: x + y – z (°C).
Giá trị của biểu thức đại số khi x = 30 °C, y = 6 °C, z = 10 °C là:
30 + 6 – 10 = 26 (°C).
Vậy nhiệt độ lúc mặt trời lặn vào buổi chiều là 26 °C.
Bài 3. Bạn Nam dự định mua 4 quyển vở có giá 5 000 đồng/quyển và 5 chiếc bút giá x đồng/ chiếc. Khi đến cửa hàng, bạn Nam thấy giá quyển vở mà bạn định mua đã giảm 20% và giá chiếc bút đã tăng 10%. Viết biểu thức T tính số tiền bạn Nam phải trả khi mua số quyển vở, bút khi đã thay đổi giá và hỏi nếu bạn Nam mang 70 000 đồng có đủ để mua số lượng đồ đó không? Biết số tiền mang đi vừa đủ để mua vở và bút như dự định khi chưa thay đổi giá.
Hướng dẫn giải
Mỗi quyển vở được giảm 20% nên quyển vở lúc này có giá bằng 100% – 20% = 80% giá niêm yết.
Giá một quyển vở khi đã giảm giá là:
5 000 . 80% = 4 000 (đồng)
Giá mua 4 quyển vở khi đã giảm giá là:
4. 4 000 = 16 000 (đồng)
Mỗi chiếc bút có giá x đồng, cửa hàng tăng giá 10% nên mỗi chiếc bút lúc này có giá bằng 100% + 10% = 110% giá niêm yết.
Giá một chiếc bút khi đã tăng giá là:
x.110% = 1,1x (đồng)
Giá mua 5 chiếc bút khi đã tăng giá là:
5. 1,1x = 5,5x (đồng)
Do đó số tiền bạn Nam phải trả khi mua 4 quyển vở và 5 chiếc bút là:
T = 16 000 + 5,5x (đồng)
Giá mua 4 quyển vở khi chưa giảm giá là:
4. 5 000 = 20 000 (đồng)
Giá mua 5 chiếc bút khi chưa tăng giá là:
5.x (đồng)
Giá tiền Nam phải trả khi mua 4 quyển vở và 5 chiếc bút khi chưa thay đổi giá là:
20 000 + 5x (đồng)
Mà bạn Nam mang 70 000 đồng đủ để mua 4 quyển vở và 5 chiếc bút khi chưa thay đổi giá nên ta có:
20 000 + 5x = 70 000 (đồng)
Suy ra 5x = 50 000
Do đó x = 10 000 (đồng)
Ta thay x = 10 000 đồng vào biểu thức T = 16 000 + 5,5x ta được:
T = 16 000 + 5,5 . 10 000 = 71 000 (đồng)
Vậy với 70 000 đồng thì bạn Nam không đủ để mau 4 quyển vở và 5 chiếc bút khi thay đổi giá.
Bài 4. Tính giá trị của các biểu thức:
a) x2y – 5 tại x = –2; y =1;
b) 2x2 – 3x + 7 tại x = 3.
Hướng dẫn giải
a) Thay x = –2; y =1 vào biểu thức x2y – 5 ta được:
(–2)2. 1 – 5 = 4 – 5 = –1
Vậy giá trị của biểu thức x2y – 5 tại x = –2; y = 1 là –1.
b) Thay x = 3 vào biểu thức 2x2 – 3x + 7 ta được:
2. 32 – 3. 3 + 7 = 2.9 – 9 + 7 = 18 – 9 + 7 = 16
Vậy giá trị của biểu thức 2x2 – 3x + 7 tại x = 3 là 16.
B.2 Bài tập trắc nghiệm
Câu 1. Trong các phát biểu sau, phát biểu nào sai?
A. 3.4 – 3.5 là biểu thức đại số;
B. 3a2 là biểu thức đại số;
C. 0 là biểu thức đại số;
D. x + y không phải là biểu thức đại số.
Hướng dẫn giải
Đáp án đúng là: D
Ta có: x + y là biểu thức đại số với biến x và y, do đó phát biểu D sai.
Vậy ta chọn phương án D.
Câu 2. Viết biểu thức đại số biểu thị tổng quãng đường đi được của một người, biết rằng người đó đi bộ trong x (giờ) với vận tốc 4 (km/h) và sau đó đi bằng xe đạp trong y (giờ) với vận tốc 18 (km/h).
A. 4(x + y);
B. 22(x + y);
C. 4y + 18x;
D. 4x + 18y.
Hướng dẫn giải
Đáp án đúng là: D
Quãng đường mà người đó đi bộ là : 4.x = 4x (km)
Quãng đường mà người đó đi bằng xe đạp là: 18.y = 18y (km)
Tổng quãng đường đi được của người đó là: 4x + 18y (km)
Vậy ta chọn phương án D.
Câu 3. Tính giá trị của biểu thức T = a. b3. c tại a = 5, b = –2, c = 6.
A. T = 240;
B. T = –240;
C. T = 30;
D. T = 12.
Hướng dẫn giải
Đáp án đúng là: B
Thay a = 5, b = –2, c = 6 vào biểu thức T đã cho ta được:
T = 5 . (–2)3 . 6 = 5 . (–8) . 6 = –240
Vậy T = –240 tại a = 5, b = –2, c = 6.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:
Lý thuyết Toán 7 Chương 5: Một số yếu tố thống kê và xác suất
Lý thuyết Bài 1: Biểu thức số. Biểu thức đại số
Lý thuyết Bài 2: Đa thức một biến. Nghiệm của đa thức một biến
Lý thuyết Bài 3: Phép cộng, phép trừ đa thức một biến
Lý thuyết Bài 4: Phép nhân đa thức một biến