Bài tập Toán lớp 7 Bài 3: Hai đường thẳng song song
A. Bài tập Hai đường thẳng song song
A.1 Bài tập tự luận
Bài 1. Cho hình vẽ sau:
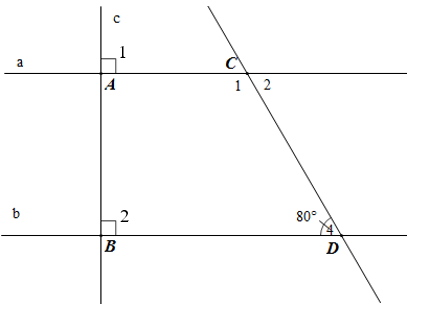 a) Vì sao a // b?
a) Vì sao a // b?
b) Tính số đo các góc C1, C2 trong hình vẽ.
Hướng dẫn giải
a) Ta có góc A1 và góc B2 là hai góc ở vị trí đồng vị, mà .
Vậy nên a // b (dấu hiệu nhận biết hai đường thẳng song song).
b) Ta có góc C1 và D4 là hai góc trong cùng phía.
Mà a // b nên
Suy ra .
Góc C2 và góc D4 ở vị trí so le trong nên .
Vậy ; .
Bài 2. Cho hình vẽ
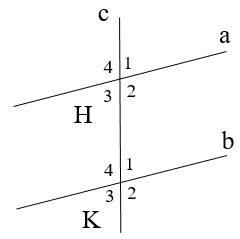
Biết Tính .
Hướng dẫn giải
Xét hai đường thẳng a và b cùng cắt đường thẳng c có: .
Mà hai góc này ở vị trí so le trong nên a // b
Suy ra (hai góc ở vị trí trong cùng phía)
Vậy .
A.2 Bài tập trắc nghiệm
Câu 1. Cho hình vẽ dưới đây:
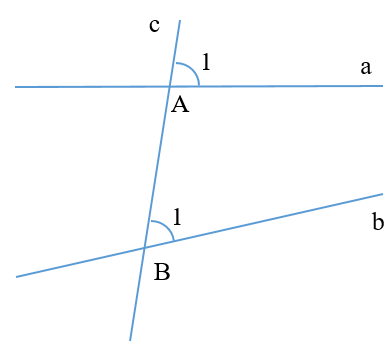
và là hai góc:
A. so le trong;
B. kề bù;
C. đồng vị;
D. kề nhau.
Hướng dẫn giải
Đáp án đúng là: C
và là hai góc đồng vị.
Câu 2. Cho hai điểm phân biệt M, N. Ta vẽ một đường thẳng a đi qua điểm M và một đường thẳng b đi qua điểm N sao cho a // b. Có thể vẽ được bao nhiêu cặp đường thẳng a, b thỏa mãn điều kiện trên.
A. Một cặp;
B. Hai căp;
C. không có cặp nào;
D. Vô số cặp.
Hướng dẫn giải
Đáp án đúng là: D
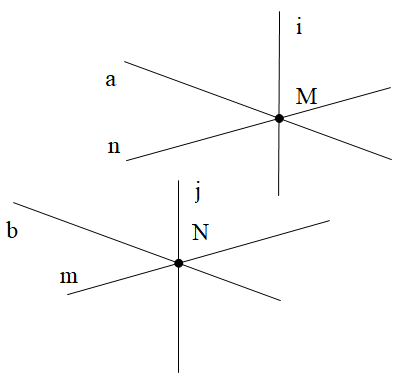 Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).
Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).
Cứ tương ứng với mỗi một đường thẳng đi qua M thì ta vẽ được một đường thẳng đi qua N và song song với đường thẳng đó (theo Tiên đề Euclid). Chẳng hạn, trên hình vẽ ta có b // a, m // n, j // i.
Vậy ta vẽ được vô số cặp đường thẳng thoả mãn yêu cầu đề bài.
Câu 3. Cho hình vẽ
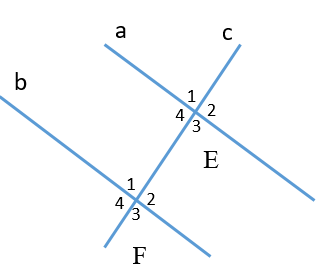
Biết a // b, . Số đo là:
A. 51°;
B. 129°;
C. 138°;
D. 48°.
Hướng dẫn giải
Đáp án đúng là: A
Ta có: và là hai góc đồng vị và a // b nên .
Mà ta lại có và là hai góc đối đỉnh nên .
Vậy
B. Lý thuyết Hai đường thẳng song song
1. Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.
Khi đó, ta thấy:
+ Góc A1 và góc B1 ở “cùng một phía” của đường thẳng c.
+ Góc A1 ở “phía trên” đường thẳng a. Góc B1 cũng ở “phía trên” đường thẳng b.
Hai góc A1 và B1 ở vị trí như thế được gọi là hai góc đồng vị.
 + Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 ở “phía dưới” của đường thẳng a. Góc B1 lại ở “phía trên” của đường thẳng b.
Hai góc A3 và B1 ở vị trí như thế gọi là hai góc so le trong.
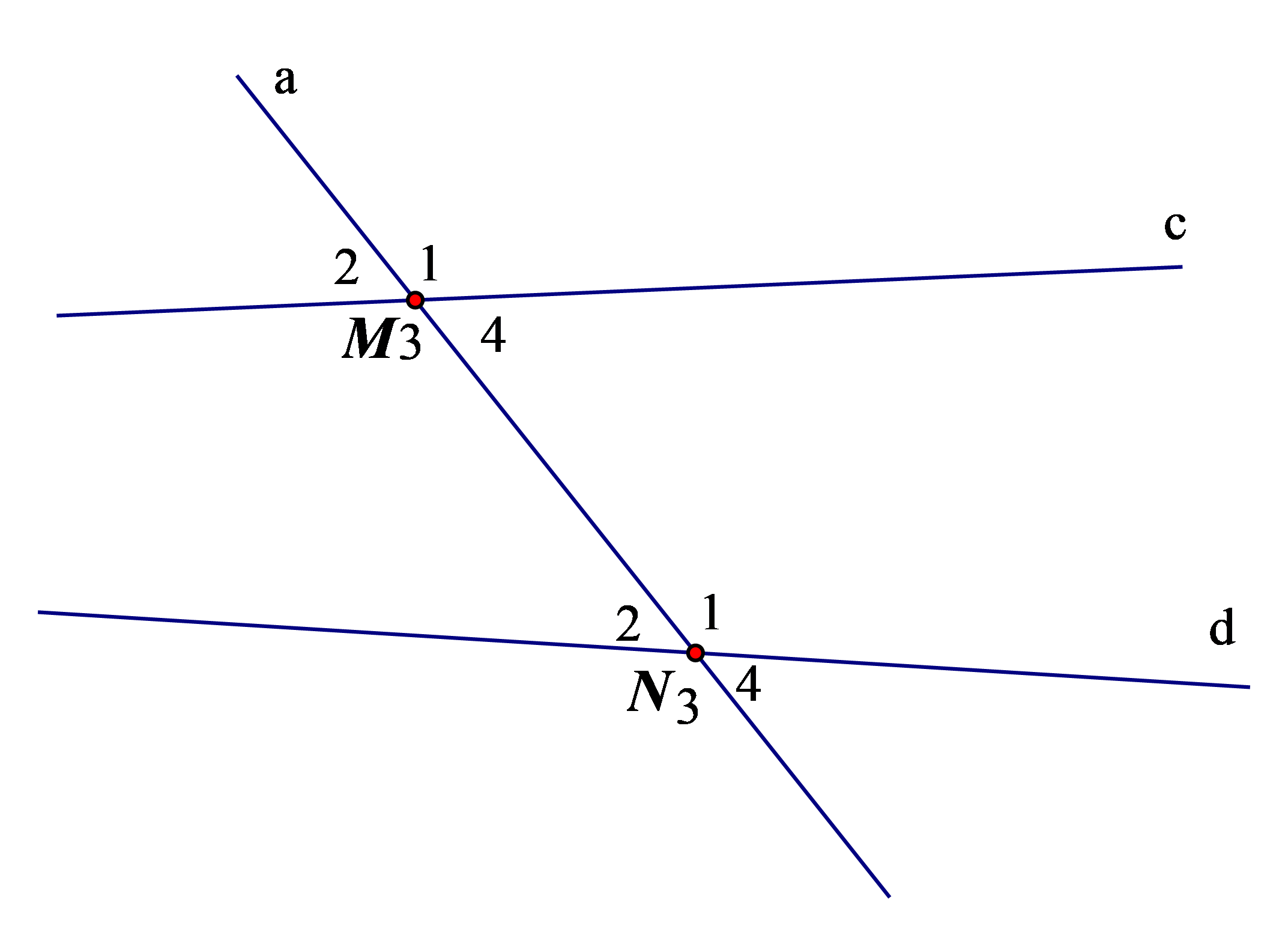
Ví dụ: Kể tên các cặp góc so le trong và đồng vị trong hình sau:
 Hướng dẫn giải
Hướng dẫn giải
Các cặp góc so le trong là: M3 và N1; M4 và N2.
Các cặp góc đồng vị là: M1 và N1; M2 và N2; M3 và N3; M4 và N4.
2. Dấu hiệu nhận biết hai đường thẳng song song
– Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
– Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.
Ví dụ:
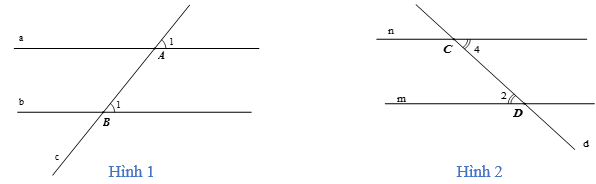
– Ở hình 1: Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau nên a // b.
– Ở hình 2: Đường thẳng d cắt hai đường thẳng m, n và trong các góc tạo thành có một cặp góc so le trong bằng nhau nên m // n.
Ví dụ: Vẽ một đường thẳng b đi qua điểm M và song song với đường thẳng a (M ∉ a) bằng êke.
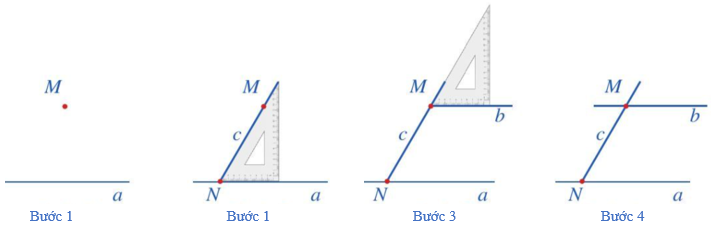 Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.
Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.
Bước 2: Đặt ê ke sao cho cạnh ngắn của góc vuông nằm trên đường thẳng a và cạnh huyền đi qua điểm M, vẽ theo cạnh huyền một phần đường thẳng c đi qua M (đường thẳng c cắt đường thẳng a tại điểm N).
Bước 3: Dịch chuyển ê ke sao cho cạnh huyền của ê ke vẫn nằm trên đường thẳng c còn cạnh ngắn của góc vuông đi qua điểm M, vẽ theo cạnh ngắn của góc vuông một phần đường thẳng b đi qua điểm M.
Bước 4: Vẽ hoàn thiện đường thẳng b.
Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.
3. Tiên đề Euclid về đường thẳng song song
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.
Ví dụ:
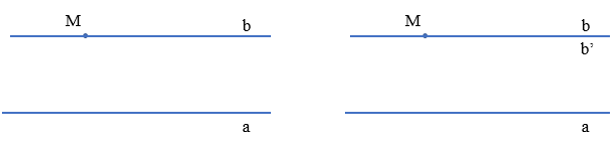 Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.
Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.
Và vẽ được đường thẳng b’ cũng đi qua M và b’ song song với a.
Khi đó theo Tiên đề Euclid thì b và b’ trùng nhau.
4. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
– Hai góc đồng vị bằng nhau.
– Hai góc so le trong bằng nhau.
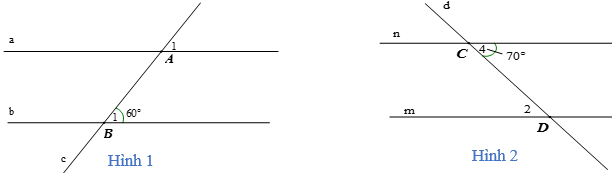
Ví dụ: Tính số đo các góc A1 và góc D2 trong hai hình vẽ sau, biết a // b và m // n.
Hướng dẫn giải
– Hình 1: Do a // b nên ta có: (hai góc đồng vị), mà nên .
Vậy .
– Hình 2: Do m // n nên: (hai góc so le trong), mà nên .
Vậy .
Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau.
+ Hai góc trong cùng phía có tổng số đo bằng 180°.
Ví dụ:
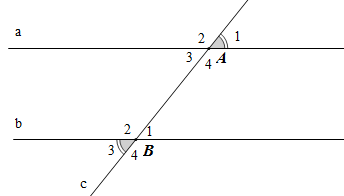
– Các cặp góc so le ngoài A1 và B3; A2 và B4; Khi đó: và .
– Hai góc trong cùng phía: góc A3 và góc B2; góc A4 và góc B1.
Khi đó: ; .