Sách bài tập Toán 7 Bài 1 (Chân trời sáng tạo): Góc và cạnh của một tam giác

Giải SBT Toán lớp 7 Bài 1: Góc và cạnh của một tam giác

Giải trang 41 Tập 2

Bài 1 trang 41 Tập 2: Tìm số đo các góc còn chưa biết của các tam giác trong Hình 5.

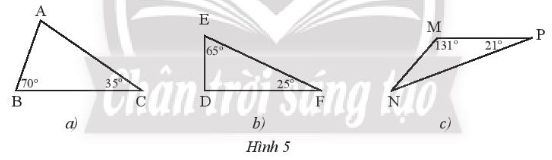
Lời giải

• Hình a)

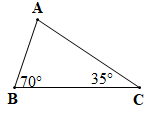
Xét DABC có: $\stackrel{︿}{\text{A}}+\stackrel{︿}{\text{B}}+\stackrel{︿}{\text{C}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{A}=180°-\widehat{C}-\widehat{B}$

Do đó $\stackrel{︿}{\text{A}}=180°-35°-70°=75°$

Vậy số đo góc A là 75°.

• Hình b)

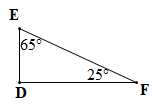
Xét DDEF có $\widehat{D}+\widehat{E}+\widehat{F}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{D}=180°-\widehat{E}-\widehat{F}$

Do đó $\stackrel{︿}{\text{D}}=180°-65°-25°=90°$

Vậy số đo góc D là 90°.

• Hình c)

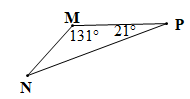
Xét DMNP có: $\stackrel{︿}{\text{M}}+\stackrel{︿}{\text{N}}+\stackrel{︿}{\text{P}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{N}=180°-\widehat{M}-\widehat{P}$

Do đó $\stackrel{︿}{N}=180°-131°-21°=28°$

Vậy số đo góc N là 28°.

Bài 2 trang 41 Tập 2:  Tính số đo x trong Hình 6.

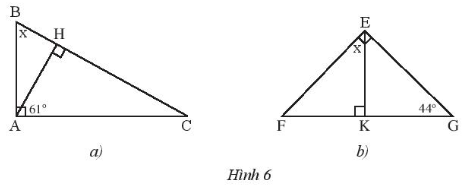
Lời giải

• Hình a)

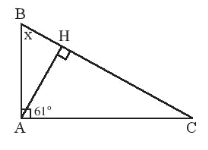
Ta có $\widehat{BAH}+\widehat{HAC}=\widehat{BAC}$ (hai góc kề nhau)

Nên $\widehat{BAH}=\widehat{BAC}-\widehat{HAC}$

Suy ra $\widehat{BAH}=90°-61°=29°$

Trong DABH vuông tại H ta có: $\widehat{B}+\widehat{BAH}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $x=90°-\widehat{BAH}=90°-29°=61°$

Vậy số đo x là 61°.

• Hình b)

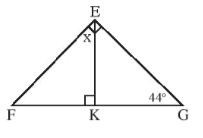
Trong DEKG vuông tại K ta có: $\widehat{G}+\widehat{KEG}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\widehat{KEG}=90°-\widehat{G}=90°-44°=46°$

Ta có $\widehat{FEK}+\widehat{KEG}=\widehat{F\text{E}G}$ (hai góc kề nhau)

Nên $\widehat{F\text{E}K}=\widehat{F\text{E}G}-\widehat{KEG}$

Suy ra x = 90° – 46° = 44°.

Vậy số đo x là 44°.

Giải trang 42 Tập 2

Bài 3 trang 42 Tập 2: Hãy tính tổng 4 góc trong một hình thoi ABCD.

Lời giải

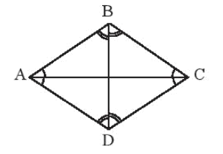
Xét DABC có: $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$ (tổng ba góc trong một tam giác) (1)

Xét DADC có: $\widehat{ADC}+\widehat{ACD}+\widehat{DAC}=180°$ (tổng ba góc trong một tam giác) (2)

Cộng hai vế của (1) và (2) ta có:

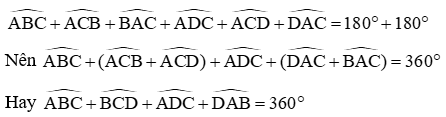
Vậy tổng bốn góc trong hình thoi ABCD bằng 360°.

Bài 4 trang 42 Tập 2: Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 1 cm, 7 cm, 9 cm;

b) 2 cm, 6 cm, 8 cm;

c) 5 cm, 6 cm, 10 cm.

Lời giải

a) Xét bộ ba độ dài: 1 cm, 7 cm, 9 cm.

Ta có: 1 + 7 = 8 < 9 không thỏa mãn bất đẳng thức tam giác nên bộ ba 1 cm, 7 cm, 9 cm không thể là độ dài ba cạnh của một tam giác.

b) Xét bộ ba độ dài: 2 cm, 6 cm, 8 cm.

Ta có: 2 + 6 = 8 không thỏa mãn bất đẳng thức tam giác nên bộ ba độ dài 2 cm, 6 cm, 8 cm không thể là độ dài ba cạnh của một tam giác.

c) Xét bộ ba độ dài: 5 cm, 6 cm, 10 cm

Ta có: 6 – 5 < 10 < 6 + 5 (do 1 < 10 < 11) thỏa mãn bất đẳng thức tam giác nên bộ ba 5 cm, 6 cm, 10 cm là độ dài ba cạnh của một tam giác.

Vậy chỉ có bộ ba 5 cm, 6 cm, 10 cm là độ dài ba cạnh của một tam giác.

Bài 5 trang 42 Tập 2: Cho tam giác ABC có BC = 9 cm, AB = 1 cm. Tìm độ dài cạnh AC, biết rằng độ dài này là một số nguyên.

Lời giải

Ta có bất đẳng thức tam giác đối với ba cạnh của tam giác ABC:

BC – AB < AC < BC + AB

Hay 9 – 1 < AC < 9 + 1

Suy ra 8 < AC < 10.

Mà độ dài của cạnh AC là một số nguyên, do đó AC = 9 (cm)

Vậy độ dài cạnh AC là 9 cm.

Bài 6 trang 42 Tập 2: Trong một trạm nghiên cứu, người ta đánh dấu ba khu vực M, N, P là ba đỉnh của một tam giác, biết các khoảng cách MN = 30 m, MP = 90 m.

a) Nếu đặt ở khu vực P một trạm phát sóng có bán kính hoạt động 60 m thì tại khu vực N có nhận được tín hiệu không? Vì sao?

b) Cùng câu hỏi như trên với bán kính hoạt động 120 m.

Lời giải

a) Hình vẽ minh họa:

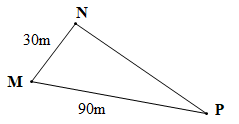
Xét tam giác MNP có MP + MN > PN > MP – MN (bất đẳng thức trong tam giác)

Hay 90 + 30 > PN > 90 – 30.

Suy ra 120 > PN > 60.

Do PN > 60 km nên với bán kính phát sóng 60m thì khu vực N không thể nhận được tín hiệu.

Vậy với bán kính phát sóng 60m thì khu vực N không thể nhận được tín hiệu.

b) Do 120 > PN > 60 nên với bán kính phát sóng 120 m, khu vực N nhận được tín hiệu.

Vậy với bán kính phát sóng 120 m, khu vực N nhận được tín hiệu.

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 7

Bài 1 : Góc và cạnh của một tam giác

Bài 2 : Tam giác bằng nhau

Bài 3 : Tam giác cân

Bài 4 : Đường vuông góc và đường xiên