Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án năm 2023

Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 1 Toán 7 Kết nối tri thức bản word có lời giải chi tiết ( cho 1 đề thi lẻ bất kì):

B1:   –

B2:   – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Giữa kì 1 Toán lớp 7 có đáp án năm 2023 – Đề 1

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ $0,0625?$

     A. $\frac{1}{4}$              B. $\frac{1}{8}$                   C. $\frac{1}{16}$               D. $\frac{1}{125}$    

Câu 2: Kết quả của phép tính: ${\left(0,08\right)}^6{.10}^6$ là:

     A. $0,8^6$                     B. $8^6$                            

C. ${10.8}^6$                        D. $0,8^{12}$             

Câu 3: So sánh $2+\sqrt{37}$ và $6+\sqrt{2}$?

A. $2+\sqrt{37}>6+\sqrt{2}$                                                                                           B.               $2+\sqrt{37}<6+\sqrt{2}$ 

C. $2+\sqrt{37}=6+\sqrt{2}$                                                                                           D. Không so sánh được

Câu 4: Chọn câu đúng:

     A. Qua điểm $A$ nằm ngoài đường thẳng $m,$ có vô số đường thẳng song song với $m.$

     B. Qua điểm $A$ nằm ngoài đường thẳng $m,$ có duy nhất một đường thẳng song song với $m.$

     C. Qua điểm $A$ nằm ngoài đường thẳng $d,$ có hai đường thẳng phân biệt cùng song song với $d.$

     D. Nếu hai đường thẳng $AB$ và $AC$ cùng song song với đường thẳng $d$ thì hai đường thẳng $AB$ và $AC$ song song với nhau.

Câu 5: Cho góc bẹt $xOy$. Vẽ tia $Oz$ nằm giữa hai tia $Ox$ và $Oy$. Vẽ tia $Om$ là phân giác của góc $xOz$. Vẽ tia $On$ là tia phân giác của góc $zOy$. Tính số đo góc $mOn?$

     A. $\mathrm{\angle }mOn={30}^0$  B. $\mathrm{\angle }mOn={60}^0$       C. $\mathrm{\angle }mOn={90}^0$      D. $\mathrm{\angle }mOn={120}^0$

Câu 6: Cho hình vẽ, biết $AE//BD,\mathrm{\angle }ABD={90}^o,\mathrm{\angle }AED={55}^o.$ Số đo góc $\mathrm{\angle }BAE$ và $\mathrm{\angle }BDE$ lần lượt là:

 

     A. ${90}^o,{55}^o$         B. ${90}^o,{125}^o$            C. ${55}^o,{90}^o$              D. ${35}^o,{55}^o$    

 

Phần II. Tự luận (7 điểm):

Bài 1: (1,5 điểm)

Thực hiện phép tính:

a) $\left(-\frac{3}{4}+\frac{2}{3}\right):\frac{5}{11}+\left(-\frac{1}{4}+\frac{1}{3}\right):\frac{5}{11}$            b) $\frac{{27}^{10}{.16}^{25}}{6^{30}{.32}^{15}}$

c) $\sqrt{144}+\sqrt{49}-25\sqrt{\frac{4}{25}}$

Bài 2: (1,5 điểm)

Tìm $x$, biết:

a) $\left(-1\frac{1}{2}\right)+\left(\frac{4}{5}+x\right)=0,5$                                                      b) ${\left(x-\frac{1}{3}\right)}^2=\frac{1}{9}$

c) $5.\sqrt{x}-\sqrt{\frac{1}{25}}=0$                                                                 

Bài 3: (1,5 điểm)

Cho hình vẽ bên dưới, biết hai đường thẳng $m$ và $n$ song song với nhau. Tính số đo các góc $\mathrm{\angle }{B}_1,\mathrm{\angle }{B}_2,\mathrm{\angle }{B}_3,\mathrm{\angle }{B}_4$?

 \

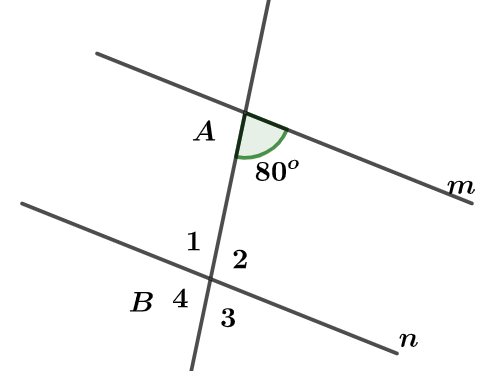Bài 4: (2 điểm)

Cho hình vẽ, biết $\mathrm{\angle }xBA={48}^o,\mathrm{\angle }BCD={48}^o,\mathrm{\angle }BAD={135}^o.$

 

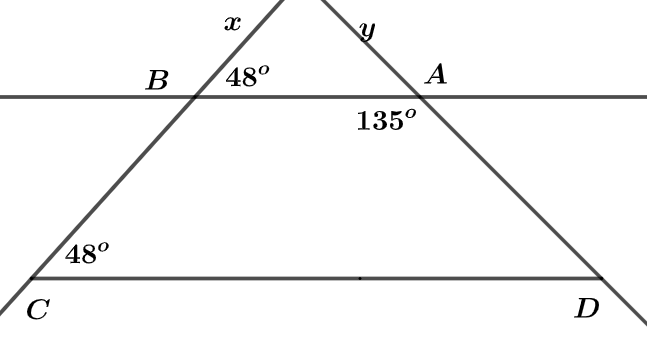
a) Chứng minh $AB//CD.$

b) Hãy tính số đo góc $\mathrm{\angle }ADC.$

Bài 5: (0,5 điểm) Tìm giá trị lớn nhất của biểu thức: $A=-\sqrt{x^2+36}+2025.$

Hướng dẫn giải:

Phần I: Trắc nghiệm

1. C

2. A

3.A

4.B

5.C

6.B

 

Câu 1:

Đưa số thập phân về phân số.

Cách giải:

Ta có: $0,0625=\frac{625}{10000}=\frac{625:625}{10000:625}=\frac{1}{16}$

Vậy phân số biểu diễn số hữu tỉ $0,0625$ là $\frac{1}{16}$.

Chọn C.

Câu 2:

Phương pháp:

Vận dụng công thức tính lũy thừa của một tích bằng tích các lũy thừa: ${\left(x.y\right)}^n=x^n.y^n$

Cách giải:

${\left(0,08\right)}^6{.10}^6={\left(0,08.10\right)}^6=0,8^6$

Chọn A.

Câu 3:

Phương pháp:

So sánh từng số hạng của tổng.

Cách giải:

Ta có: $2=\sqrt{2^2}=\sqrt{4};6=\sqrt{6^2}=\sqrt{36}$

Vì $4>2$ nên $\sqrt{4}>\sqrt{2}$ hay $2>\sqrt{2}$

     $37>36$ nên $\sqrt{37}>\sqrt{36}$ hay $\sqrt{37}>6$

Do đó, $2+\sqrt{37}>6+\sqrt{2}$

Chọn A.

Câu 4:

Phương pháp:

Tiên đề Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đướng thẳng đó.

Cách giải:

     A. Qua điểm $A$ nằm ngoài đường thẳng $m,$ có vô số đường thẳng song song với $m.$ $\Rightarrow$ Sai

     B. Qua điểm $A$ nằm ngoài đường thẳng $m,$ có duy nhất một đường thẳng song song với $m.$ $\Rightarrow$ Đúng

     C. Qua điểm $A$ nằm ngoài đường thẳng $d,$ có hai đường thẳng phân biệt cùng song song với $d.$$\Rightarrow$ Sai

     D. Nếu hai đường thẳng $AB$ và $AC$ cùng song song với đường thẳng $d$ thì hai đường thẳng $AB$ và $AC$ song song với nhau. $\Rightarrow$ Sai

Chọn B.

Câu 5:

Phương pháp:

$Oz$ là tia phân giác của góc $xOy$ thì ta có: $\mathrm{\angle }xOz=\mathrm{\angle }zOy=\frac{\mathrm{\angle }xOy}{2}$

Cách giải:

 

Vì $Om$ là tia phân giác của góc $xOz$ nên $\mathrm{\angle }zOm=\frac{\mathrm{\angle }xOz}{2}$ hay $\mathrm{\angle }xOz=2.\mathrm{\angle }zOm$

Vì $On$ là tia phân giác của góc $zOy$ nên $\mathrm{\angle }nOz=\frac{\mathrm{\angle }zOy}{2}$ hay $\mathrm{\angle }zOy=2.\mathrm{\angle }nOz$

Vì $\mathrm{\angle }xOz$ và $\mathrm{\angle }zOy$ là hai góc kề bù nên $\mathrm{\angle }xOy+\mathrm{\angle }zOy={180}^0$

$\begin{array}{l}\Rightarrow 2.\mathrm{\angle }zOm+2.\mathrm{\angle }nOz={180}^0\\ \Rightarrow 2.\left(\mathrm{\angle }zOm+\mathrm{\angle }nOz\right)={180}^0\\ \Rightarrow \mathrm{\angle }zOm+\mathrm{\angle }nOz={180}^0:2\\ \Rightarrow \mathrm{\angle }zOm+\mathrm{\angle }nOz={90}^0\end{array}$

Vì $Oz$ nằm giữa hai tia $Om$ và $On$ nên $\mathrm{\angle }zOm+\mathrm{\angle }nOz=\mathrm{\angle }mOn={90}^0$

Vậy $\mathrm{\angle }mOn={90}^0$

Chọn C.

Câu 6:

Phương pháp:

– Nếu một đường thẳng cắt hai đường thẳng song song thì:

          + Hai góc so le trong bằng nhau;

          + Hai góc đồng vị bằng nhau.

– Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt đường thẳng phân biệt ab, và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng hai thì a và b song song với nhau.

– Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì sẽ vuông góc với đường thẳng còn lại.

Cách giải:

 

Ta có $\mathrm{\angle }ABD={90}^o\left(gt\right)\Rightarrow AB\mathrm{\perp }BD$

Mà $AE//BD\left(gt\right)$

$\Rightarrow AE\mathrm{\perp }AB\Rightarrow \mathrm{\angle }BAE={90}^o$

Vì $AE//BD\Rightarrow \mathrm{\angle }EDx=\mathrm{\angle }AED={55}^o$ (đối đỉnh)

Mà $\mathrm{\angle }BDE+\mathrm{\angle }EDx={180}^o$ (hai góc kề bù)

$\Rightarrow \mathrm{\angle }BDE={180}^o-{55}^o={125}^o$

Chọn B.

 

Phần II. Tự luận:

Bài 1:

Phương pháp:

a) Thực hiện các phép toán với các số hữu tỉ, sử dụng tính chất phân phối của phép nhân đối với phép cộng: $a.c+b.c=c.\left(a+b\right)$

b) Vận dụng quy tắc tính lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: ${\left(x^m\right)}^n=x^{m.n}$.

Vận dụng quy tắc tính thương của hai lũy thừa cùng cơ số: $x^m:x^n=x^{m-n}\left(x\ne 0;m\ge n\right)$.

d) Tính căn bậc hai của một số thực: $\sqrt{a^2}=a(a\ge 0)$

Cách giải:

 

a) $\left(-\frac{3}{4}+\frac{2}{3}\right):\frac{5}{11}+\left(-\frac{1}{4}+\frac{1}{3}\right):\frac{5}{11}$

$\begin{array}{l}=\left(-\frac{3}{4}+\frac{2}{3}\right).\frac{11}{5}+\left(-\frac{1}{4}+\frac{1}{3}\right).\frac{11}{5}\\ =\left(-\frac{3}{4}+\frac{2}{3}+\frac{-1}{4}+\frac{1}{3}\right).\frac{11}{5}\\ =\left[\left(-\frac{3}{4}+\frac{-1}{4}\right)+\left(\frac{2}{3}+\frac{1}{3}\right)\right].\frac{11}{5}\\ =\left(\frac{-4}{4}+\frac{3}{3}\right).\frac{11}{5}\\ =\left(-1+1\right).\frac{11}{5}\\ =0.\frac{11}{5}=0\end{array}$

b)

$\frac{{27}^{10}{.16}^{25}}{6^{30}{.32}^{15}}$

$\begin{array}{l}=\frac{{\left(3^3\right)}^{10}.{\left(2^4\right)}^{25}}{{\left(2.3\right)}^{30}.{\left(2^5\right)}^{15}}=\frac{3^{3.10}{.2}^{4.25}}{2^{30}{.3}^{30}{.2}^{5.15}}\\ =\frac{3^{30}{.2}^{100}}{2^{30}{.3}^{30}{.2}^{75}}=\frac{2^{100}}{2^{30+75}}\\ =\frac{2^{100}}{2^{105}}=\frac{1}{2^5}=\frac{1}{32}\end{array}$

 

 

c)

$\begin{array}{l}\sqrt{144}+\sqrt{49}-25\sqrt{\frac{4}{25}}\\ =12+7-25.\frac{2}{5}\\ =19-10\\ =9\end{array}$

Bài 2:

Phương pháp:

a) Thực hiện các phép toán với số hữu tỉ, vận dụng quy tắc chuyển vế tìm $x$

b) Giải ${\left[A\left(x\right)\right]}^2=a^2={\left(-a\right)}^2$

 

Trường hợp 1: $A\left(x\right)=a$

Trường hợp 2: $A\left(x\right)=-a$

c) Vận dụng kiến thức căn bậc hai số học của số thực, tìm $x$

d) $\left|x\right|=a$

Trường hợp $a<0$, khi đó phương trình không có nghiệm $x$

Trường hợp $a>0$, vận dụng kiến thức giá trị tuyệt đối của một số thực: $\left|x\right|=\{\begin{array}{l}xkhix>0\\ -xkhix<0\\ 0khix=0\end{array}$

Cách giải:

a) $\left(-1\frac{1}{2}\right)+\left(\frac{4}{5}+x\right)=0,5$

$\begin{array}{l}\frac{-3}{2}+\frac{4}{5}+x=\frac{1}{2}\\ x=\frac{1}{2}-\left(-\frac{3}{2}\right)-\frac{4}{5}\\ x=\frac{1}{2}+\frac{3}{2}-\frac{4}{5}\\ x=\frac{4}{2}-\frac{4}{5}\\ x=2-\frac{4}{5}\\ x=\frac{10}{5}-\frac{4}{5}\\ x=\frac{6}{5}\end{array}$

Vậy $x=\frac{6}{5}$

b) ${\left(x-\frac{1}{3}\right)}^2=\frac{1}{9}$

${\left(x-\frac{1}{3}\right)}^2={\left(\frac{1}{3}\right)}^2={\left(-\frac{1}{3}\right)}^2$

Trường hợp 1: $\begin{array}{l}x-\frac{1}{3}=\frac{1}{3}\\ x=\frac{1}{3}+\frac{1}{3}\\ x=\frac{2}{3}\end{array}$

Trường hợp 2: $\begin{array}{l}x-\frac{1}{3}=-\frac{1}{3}\\ x=\frac{-1}{3}+\frac{1}{3}\\ x=0\end{array}$

Vậy $x\in \left\{\frac{2}{3};0\right\}$

c) $5.\sqrt{x}-\sqrt{\frac{1}{25}}=0$

$\begin{array}{l}5.\sqrt{x}-\frac{1}{5}=0\\ 5.\sqrt{x}=\frac{1}{5}\\ \sqrt{x}=\frac{1}{5}:5=\frac{1}{5}.\frac{1}{5}=\frac{1}{25}\end{array}$

$\begin{array}{l}\sqrt{x}=\sqrt{{\left(\frac{1}{25}\right)}^2}\\ \Rightarrow x=\frac{1}{625}\end{array}$

Vậy $x=\frac{1}{625}$

Bài 3:

Phương pháp:

– Nếu một đường thẳng cắt hai đường thẳng song song thì:

          + Hai góc so le trong bằng nhau;

          + Hai góc đồng vị bằng nhau.

Cách giải:

 

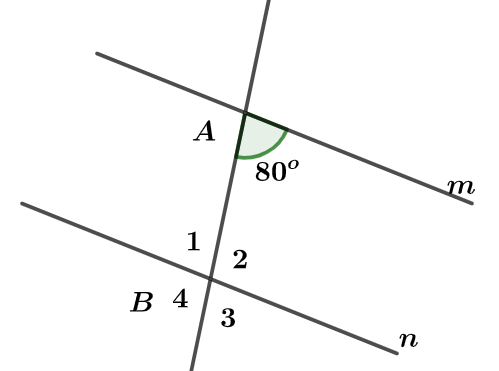
Vì $m//n\Rightarrow \mathrm{\angle }{B}_1=\mathrm{\angle }mAB={80}^o$ (hai góc so le trong)

Mà $\mathrm{\angle }{B}_1+\mathrm{\angle }{B}_2={180}^o$ (hai góc kề bù) $\Rightarrow \mathrm{\angle }{B}_2={180}^o-\mathrm{\angle }{B}_1={180}^o-{80}^o={100}^o$

Mà $\mathrm{\angle }{B}_3=\mathrm{\angle }{B}_1$ (hai góc đối đỉnh) $\Rightarrow \mathrm{\angle }{B}_3={80}^o$

Tương tự $\mathrm{\angle }{B}_4=\mathrm{\angle }{B}_2={100}^o.$

Bài 4:

Phương pháp:

– Nếu một đường thẳng cắt hai đường thẳng song song thì:

          + Hai góc so le trong bằng nhau;

          + Hai góc đồng vị bằng nhau.

– Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt đường thẳng phân biệt ab, và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng hai thì a và b song song với nhau.

Cách giải:

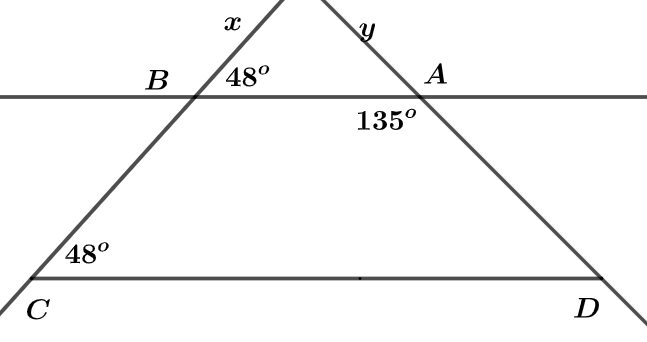
a) Ta có $\mathrm{\angle }xBA={48}^o,\mathrm{\angle }BCD={48}^o\left(gt\right)$

$\Rightarrow \mathrm{\angle }xBA=\mathrm{\angle }BCD\left(={48}^o\right)$

Mà hai góc trên ở vị trí đồng vị

$\Rightarrow AB//CD\left(dhnb\right)$

b) Vì $AB//CD\left(cmt\right)\Rightarrow \mathrm{\angle }yAB=\mathrm{\angle }ADC$ (hai góc đồng vị)

Ta lại có:

$\mathrm{\angle }yAB+\mathrm{\angle }BAD={180}^o$ (hai góc kề bù)

$\mathrm{\angle }yAB+{135}^o={180}^o\Rightarrow \mathrm{\angle }yAB={180}^o-{135}^o={45}^o$

$\Rightarrow \mathrm{\angle }ADC=\mathrm{\angle }yAB={45}^o.$

Bài 5:

Phương pháp:

Đánh giá biểu thức $A\le k\left(k\in \mathbb{R}\right)\Rightarrow MaxA=k$

Chú ý: Bình phương 1 số luôn lớn hơn hoặc bằng 0

Cách giải:

Ta có: $x^2\ge 0$ với mọi số thực $x$ nên $x^2+36\ge 36$ với mọi số thực $x$.

Suy ra $\sqrt{x^2+49}\ge \sqrt{49}=7$ với mọi số thực $x$.

Do đó, $-\sqrt{x^2+49}\le -7$ với mọi số thực $x$.

Suy ra $A=-\sqrt{x^2+49}+2023\le -7+2023=2016$ hay $A\le 2016$ với mọi số thực $x$.

Dấu “=” xảy ra $\iff$$x^2=0$$\iff$$x=0$.

Vậy $MaxA=2016$ khi x = 0

Đề thi Giữa kì 1 Toán lớp 7 có đáp án năm 2023 – Đề 2

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

Câu 1. Khẳng định nào sau đây đúng nhất:

Nếu a ∈ℤ thì

A. a ∈ ℝ;

B. a ∈ℚ;

C. Cả A và B đều đúng.

D. Cả A và B đều sai.

Câu 2. Trong các số sau, số nào không phải là số đối của số $-\frac{3}{2}$?

A. 1,5;

B. $\frac{15}{10}$;

C. ‒1,5;

D. ‒(‒1,5).

Câu 3. Cho các số hữu tỉ sau $\frac{-12}{17};\frac{-3}{17};\frac{-1}{17};\frac{-9}{17}$. Sắp xếp các số trên theo thứ tự giảm dần ta được:

A. $\frac{-12}{17};\frac{-3}{17};\frac{-1}{17};\frac{-9}{17}$;

B. $\frac{-1}{17};\frac{-3}{17};\frac{-9}{17};\frac{-12}{17}$;

C. $\frac{-3}{17};\frac{-12}{17};\frac{-1}{17};\frac{-9}{17}$;

D. $\frac{-12}{17};\frac{-9}{17};\frac{-3}{17};\frac{-1}{17}$.

Câu 4. Điểm A trên trục số trong hình vẽ dưới đây biểu diễn số hữu tỉ nào?

A. $-\frac{1}{5}$;

B. $-\frac{2}{5}$;

C. $-\frac{3}{5}$;

D. $-\frac{4}{5}$.

Câu 5. Trong các số sau đây số nào là số thập phân vô hạn không tuần hoàn:

A. 1,(3);

B. 1,2(21);

C. 1,11111…;

D. 2,64575…

Câu 6. Căn bậc hai số học của số a không âm là:

A. $\sqrt{a};$

B. $-\sqrt{a};$

C. $\sqrt{a}$ và $-\sqrt{a};$

D. Không có đáp án.

Câu 7. Cho x = -12. Tính |x + 2|.

A. 10;

B. -10;

C. 12;

D. -12.

Câu 8. Khẳng định nào sau đây là đúng?

A. Chỉ có một giá trị x thỏa mãn x² = 3 được biểu diễn bởi điểm nằm trước điểm 0, cách 0 một đoạn bằng $\sqrt{3}$ trên trục số;

B. Chỉ có một giá trị x thỏa mãn x² = 3 được biểu diễn bởi điểm nằm sau điểm 0, cách 0 một đoạn bằng $\sqrt{3}$ trên trục số;

C. Có hai giá trị x thỏa mãn x² = 3 được biểu diễn bởi hai điểm, một điểm nằm trước và một điểm nằm sau điểm 0, hai điểm đều cách điểm 0 một khoảng bằng $\sqrt{3}$ trên trục số;

D. Không có giá trị nào của x thỏa mãn x² = 3.

Câu 9. Cho hình vẽ sau:

Số cặp góc kề bù (không kể góc bẹt) có trong hình vẽ trên là

A. 1;

B. 2;

C. 3;

D. 4.

Câu 10. Cho $\widehat{xOy}=120°$, tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:

A.120°;

B. 80°;

C. 60°;

D.150°.

Câu 11. Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:

A. Hai đường thẳng đó trùng nhau;

B. Hai đường thẳng cắt nhau tại A;

C. Hai đường thẳng song song;

D. Hai đường thẳng vuông góc.

Câu 12. Cho định lí sau: “Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”

Giả thiết và kết luận cho định lí trên là:

A.

B.

C.

D.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Biết biểu thức 6⁸ . 12⁵ viết được dưới dạng 2^a . 3^b. Tính a – b.

b) Cho a = $\sqrt{99}$ = 9,94987471… và b = 5,(123).

i) Hai số b là số thập phân hữu hạn, số thập phân vô hạn tuần hoàn hay số vô tỉ? Tìm chữ số thập phân thứ năm của số b.

ii) Ước lượng tích của a và b.

Bài 2. (1,5 điểm) Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):

a) $2^4+8.{\left({\left(-2\right)}^2:\frac{1}{2}\right)}^0-\frac{1}{2^2}.4+{\left(-2\right)}^2$;

b) $\frac{1}{2023}.\frac{-7}{9}+\frac{2022}{2023}.\frac{-7}{9}+\frac{7}{9}$;

c) $-1\frac{2}{3}-{\left(\sqrt{0,25}\right)}^2+\frac{8}{3}-\sqrt{\frac{49}{16}}+\frac{3}{2}$.

Bài 3. (1,5 điểm) Tìm x, biết:

a) $\left(x-\frac{1}{4}\right):\frac{1}{2}=\frac{-8}{5}$;      b) ${\left(\frac{1}{3}\right)}^{2x-1}=\frac{1}{243}$;      c)  – 2 = $–\frac{1}{4}$.

Bài 4. (2,0 điểm)

Cho ba đường thẳng a, b, c như hình vẽ sau:

Biết ${\hat{A}}_1=2{\hat{B}}_1$ và ${\hat{A}}_1,{\hat{B}}_1$ là hai góc bù nhau.

a) Viết giả thiết và kết luận của bài toán.

b) Tính số đo ${\hat{A}}_1,{\hat{B}}_1$, từ đó chứng minh a // b.

c) Tia phân giác của góc A₁ cắt đường thẳng b tại C. Tính số đo góc ACB.

Bài 5. (0,5 điểm) Tính giá trị của biểu thức:

$H=\frac{38}{50}+\frac{9}{20}-\frac{11}{30}+\frac{13}{42}-\frac{15}{56}+\frac{17}{72}-\mathrm{\dots }+\frac{197}{9702}-\frac{199}{9900}$.

ĐÁP ÁN & HƯỚNG DẪN GIẢI

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	C	C	B	C	D	A	A	C	B	C	A	A

Hướng dẫn giải phần trắc nghiệm

Câu 1.

Đáp án đúng là: C

Với mọi a ∈ℤ ta đều có thể viết được dưới dạng $\frac{\text{a}}{\text{1}}$ nên a ∈ ℚ.

Mọi số nguyên, số hữu tỉ đều là số thực nên a ∈ ℝ.

Vậy ta chọn phương án C.

Câu 2.

Đáp án đúng là: C

Ta có $-\frac{3}{2}=-1,5$ nên ‒1,5 không phải là số đối của số $-\frac{3}{2}$.

Vậy ta chọn phương án C.

Câu 3.

Đáp án đúng là: B

Vì ‒1 > ‒3 > ‒9 > ‒12

Nên $\frac{-1}{17}>\frac{-3}{17}>\frac{-9}{17}>\frac{-12}{17}$ (so sánh các phân số cùng mẫu)

Nên sắp xếp theo thứ tự giảm dần ta được dãy: $\frac{-1}{17};\frac{-3}{17};\frac{-9}{17};\frac{-12}{17}$.

Câu 4.

Đáp án đúng là: C

Quan sát trục số ta thấy đoạn thẳng đơn vị từ 0 đến 1 chia thành 5 đoạn bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng $\frac{1}{5}$ đơn vị cũ.

Điểm A nằm bên trái 0 và cách 0 một đoạn bằng 3 đơn vị mới nên điểm A biểu diễn số $-\frac{3}{5}$.

Câu 5.

Đáp án đúng là: D

Số 2,64575… là số thập phân vô hạn và có phần thập phân không lặp lại theo một chu kì nào.

Do đó số 2,64575… là số thập phân vô hạn không tuần hoàn.

Câu 6.

Đáp án đúng là: A

Căn bậc hai số học của một số a không âm là $\sqrt{a}.$

Ta chọn phương án A.

Câu 7.

Đáp án đúng là: A

Với x = -12, ta có:

|x + 2| = |-12 + 2| = | -10| = -(-10) = 10.

Câu 8.

Đáp án đúng là: C

Ta có: x² = 3.

Suy ra $x=\pm \sqrt{3}$.

Biểu diễn các số thực x trên trục số là:

Nhìn vào trục số ta thấy điểm biểu diễn $-\sqrt{3}$ nằm trước điểm 0 trên trục số; điểm biểu diễn $\sqrt{3}$ nằm sau điểm 0 trên trục số.

Hai số $-\sqrt{3}$và $\sqrt{3}$cách số 0 một khoảng bằng nhau và bằng $\sqrt{3}$ trên trục số.

Vậy chọn phương án C.

Câu 9.

Đáp án đúng là: B

Các cặp góc kề bù (không kể góc bẹt) có trong hình vẽ trên là: $\widehat{aOb}$ và $\widehat{bOd}$; $\widehat{aOc}$ và $\widehat{cOd}$.

Vậy có 2 cặp góc kề bù với nhau.

Câu 10.

Đáp án đúng là: C

Ta có Ot là tia phân giác góc xOy

Suy ra $\widehat{xOt}=\widehat{yOt}=\frac{\widehat{xOy}}{2}=\frac{120°}{2}=60°$.

Câu 11.

Đáp án đúng là: A

Theo tiên đề Euclid ta có: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó

Do đó, qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì hai đường thẳng đó phải trùng nhau.

Vậy t chọn phương án A.

Câu 12.

Đáp án đúng là: A

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Ta có:

6⁸ . 12⁵ = (2 . 3)⁸ . (3. 2²)⁵ = 2⁸ . 3⁸ . 3⁵ . (2²)⁵

= 2⁸ . 2^{2 . 5} . 3^{8 + 5} = 2^{8 + 10} . 3¹³ = 2¹⁸ . 3¹³.

Khi đó a = 18 và b = 13.

Do đó a – b = 18 – 13 = 5.

Vậy a – b = 5.

b)

i) Số b = 5,(123) = 5,12312312… là số thập phân vô hạn tuần hoàn có chu kì là 123.

Chữ số thập phân thứ năm của số b là chữ số 2.

ii) Làm tròn a = $\sqrt{99}$ = 9,94987471… đến hàng đơn vị ta được a ≈ 10.

Làm tròn b = 5,12312312… đến hàng đơn vị ta được b ≈ 5.

Khi đó ước lượng tích của a và b là a . b ≈ 10 . 5 = 50.

Bài 2. (1,5 điểm)

a) $2^4+8.{\left({\left(-2\right)}^2:\frac{1}{2}\right)}^0-\frac{1}{2^2}.4+{\left(-2\right)}^2$

$=16+8.1-\frac{1}{4}.4+4$

= 16 + 8 – 1 + 4

= 27

b) $\frac{1}{2023}.\frac{-7}{9}+\frac{2022}{2023}.\frac{-7}{9}+\frac{7}{9}$

$=\frac{1}{2023}.\frac{-7}{9}+\frac{2022}{2023}.\frac{-7}{9}+\frac{-7}{9}.\left(-1\right)$

$=\frac{-7}{9}.\left(\frac{1}{2023}+\frac{2022}{2023}-1\right)$

$=\frac{-7}{9}.\left(\frac{2023}{2023}-1\right)=\frac{-7}{9}.\left(1-1\right)=\frac{-7}{9}.0=0$.

c) $-1\frac{2}{3}-{\left(\sqrt{0,25}\right)}^2+\frac{8}{3}-\sqrt{\frac{49}{16}}+\frac{3}{2}$

$=-\frac{5}{3}-0,25+\frac{8}{3}-\sqrt{{\left(\frac{7}{4}\right)}^2}+\frac{3}{2}$

$=-\frac{5}{3}-\frac{1}{4}+\frac{8}{3}-\frac{7}{4}+\frac{3}{2}$

$=\left(-\frac{5}{3}+\frac{8}{3}\right)+\left(-\frac{1}{4}-\frac{7}{4}\right)+\frac{3}{2}$

$=\frac{3}{3}+\frac{-8}{4}+\frac{2}{2}+\frac{1}{2}$

$=1+\left(-2\right)+1+\frac{1}{2}$

$=\frac{1}{2}$

Bài 3. (1,5 điểm)

a) $\left(x-\frac{1}{4}\right):\frac{1}{2}=\frac{-8}{5}$

$x-\frac{1}{4}=\frac{-8}{5}.\frac{1}{2}$

$x-\frac{1}{4}=\frac{-4}{5}$

$x=\frac{-4}{5}+\frac{1}{4}$

$x=\frac{-16}{20}+\frac{5}{20}$

$x=\frac{-11}{20}$

Vậy $x=\frac{-11}{20}$.

b) ${\left(\frac{1}{3}\right)}^{2x-1}=\frac{1}{243}$

${\left(\frac{1}{3}\right)}^{2x-1}=\frac{1}{3^5}$.

${\left(\frac{1}{3}\right)}^{2x-1}={\left(\frac{1}{3}\right)}^5$.

Suy ra 2x – 1 = 5.

2x = 5 + 1.

2x = 6.

x = 6 : 2.

x = 3.

Vậy x = 3.

c)  – 2 = $–\frac{1}{4}$

 = $–\frac{1}{4}$ + 2

 = $–\frac{1}{4}$ + $\frac{8}{4}$

 = $\frac{7}{4}$

Trường hợp 1: $x+\frac{2}{5}=\frac{7}{4}$

$x=\frac{7}{4}-\frac{2}{5}$

$x=\frac{35}{20}-\frac{8}{20}$

$x=\frac{27}{20}$

Trường hợp 2: $x+\frac{2}{5}=-\frac{7}{4}$

$x=-\frac{7}{4}-\frac{2}{5}$

$x=-\frac{35}{20}-\frac{8}{20}$

$x=-\frac{43}{20}$

Vậy có hai giá trị x thoả mãn là $x=\frac{27}{20}$; $x=-\frac{43}{20}$.

Bài 4. (2,0 điểm)

a)

b) • Do ${\hat{A}}_1,{\hat{B}}_1$ là hai góc bù nhau nên ${\hat{A}}_1+{\hat{B}}_1=180°$

Mà ${\hat{A}}_1=2{\hat{B}}_1$ (giả thiết) nên ta có $2{\hat{B}}_1+{\hat{B}}_1=180°$

Hay $3{\hat{B}}_1=180°$

Do đó ${\hat{B}}_1=180°:3=60°$

Suy ra ${\hat{A}}_1=2{\hat{B}}_1=2.60°=120°.$

• Ta có ${\hat{B}}_1+{\hat{B}}_2={180}^o$ (hai góc kề bù).

Suy ra ${\hat{B}}_2={180}^o-{\hat{B}}_1={180}^o-{60}^o={120}^o$

Do đó ${\hat{A}}_1={\hat{B}}_2$ (cùng bằng 120°).

Mà hai góc này ở vị trí so le trong.

Suy ra a // b (dấu hiệu nhận biết).

Vậy a // b.

c) Vì AC là tia phân giác của góc A₁ nên ta có:

$\widehat{xAC}=\widehat{BAC}=\frac{1}{2}{\hat{A}}_1=\frac{1}{2}.120°=60°$ (tính chất tia phân giác).

Mà a // b (chứng minh câu b)

Do đó $\widehat{ACB}=\widehat{xAC}=60°$ (hai góc so le trong).

Vậy $\widehat{ACB}=60°.$

Bài 5. (0,5 điểm)

Ta có:

$\frac{9}{20}=\frac{9}{4.5}=\frac{5+4}{4.5}=\frac{5}{4.5}+\frac{4}{4.5}=\frac{1}{4}+\frac{1}{5}$

$\frac{11}{30}=\frac{11}{5.6}=\frac{6+5}{5.6}=\frac{6}{5.6}+\frac{5}{5.6}=\frac{1}{5}+\frac{1}{6}$

$\frac{13}{42}=\frac{13}{6.7}=\frac{7+6}{6.7}=\frac{7}{6.7}+\frac{6}{6.7}=\frac{1}{6}+\frac{1}{7}$

…

$\frac{197}{9702}=\frac{197}{98.99}=\frac{99+98}{98.99}=\frac{99}{98.99}+\frac{98}{98.99}=\frac{1}{98}+\frac{1}{99}$

$\frac{199}{9900}=\frac{199}{99.100}=\frac{100+99}{99.100}=\frac{100}{99.100}+\frac{99}{99.100}=\frac{1}{99}+\frac{1}{100}$

Do đó $H=\frac{38}{50}+\frac{9}{20}-\frac{11}{30}+\frac{13}{42}-\frac{15}{56}+\frac{17}{72}-\mathrm{\dots }+\frac{197}{9702}-\frac{199}{9900}$

$=\frac{38}{50}+\left(\frac{1}{4}+\frac{1}{5}\right)-\left(\frac{1}{5}+\frac{1}{6}\right)+\left(\frac{1}{6}+\frac{1}{7}\right)-\left(\frac{1}{7}+\frac{1}{8}\right)$

$+\left(\frac{1}{8}+\frac{1}{9}\right)-\mathrm{\dots }+\left(\frac{1}{98}+\frac{1}{99}\right)-\left(\frac{1}{99}+\frac{1}{100}\right)$

$=\frac{38}{50}+\frac{1}{4}+\frac{1}{5}-\frac{1}{5}-\frac{1}{6}+\frac{1}{6}+\frac{1}{7}-\frac{1}{7}-\frac{1}{8}+\frac{1}{8}+\frac{1}{9}$

$-\mathrm{\dots }+\frac{1}{98}+\frac{1}{99}-\frac{1}{99}-\frac{1}{100}$

$=\frac{38}{50}+\frac{1}{4}+\left(\frac{1}{5}-\frac{1}{5}\right)+\left(-\frac{1}{6}+\frac{1}{6}\right)+\left(\frac{1}{7}-\frac{1}{7}\right)+\left(-\frac{1}{8}+\frac{1}{8}\right)$

$+\left(\frac{1}{9}-\frac{1}{9}\right)+\mathrm{\dots }+\left(-\frac{1}{98}+\frac{1}{98}\right)+\left(\frac{1}{99}-\frac{1}{99}\right)-\frac{1}{100}$

$=\frac{38}{50}+\frac{1}{4}+0+0+0+0+0+\mathrm{\dots }+0+0-\frac{1}{100}$

$=\frac{38}{50}+\frac{1}{4}-\frac{1}{100}$

$=\frac{76}{100}+\frac{25}{100}-\frac{1}{100}$

$=\frac{76+25-1}{100}$

$=\frac{100}{100}$

= 1.

Vậy H = 1.

A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ 1

STT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ kiến thức, kĩ năng cần kiềm tra, đánh giá								Tổng điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
			TN	TL	TN	TL	TN	TL	TN	TL
1	Số hữu tỉ (14 tiết)	Tập hợp các số hữu tỉ. Thứ tự thực hiện các phép tính.	3 (0,5đ)		1 (0,25đ)						4
		Các phép toán với số hữu tỉ				1 (0,5đ)		4 (2 đ)		1 (0,5đ)
2	Số thực (10 tiết)	Số thập phân vô hạn tuần hoàn. Số vô tỉ. Căn bậc hai số học	2 (0,5đ)			1 (1đ)					3
		Tập hợp các số thực	2 (0,5đ)					2 (1 đ)
3	Góc và đường thẳng song song (11 tiết)	Góc ở vị trí đặc biệt. Tia phân giác của một góc	2 (0,5đ)					1 (0,5đ)			3
		Dấu hiệu nhận biết và tính chất hai đường thẳng song song. Tiên đề Euclid.	1 (0,25đ)					2 (1đ)
		Định lí và chứng minh định lí	1 (0,25đ)	1 (0,5đ)
Tổng: Số câu Điểm			11 (2,75đ)	1 (0,5đ)	1 (0,25đ)	2 (1,5đ)	0 (0 đ)	9 (4,5đ)	0 (0 đ)	1 (0,5đ)	10
Tỉ lệ			32,5%		1,75%		45%		5%
Tỉ lệ chung			50%				50%

 

B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1

STT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ kiến thức, kĩ năng cần kiềm tra, đánh giá	Số câu hỏi theo mức độ
				Nhận biết	Thông hiểu	Vận dụng	Vận dụng cao
1	Số hữu tỉ	Tập hợp các số hữu tỉ. Thứ tự thực hiện các phép tính.	Nhận biết: – Nhận biết được số hữu tỉ. – Nhận biết được tập hợp các số hữu tỉ ℚ. – Nhận biết được số đối của số hữu tỉ. – Nhận biết được thứ tự trong tập hợp số hữu tỉ.	3 (TN1,TN2, TN3)
			Thông hiểu: – Biểu diễn số hữu tỉ trên trục số.	1 (TN4)
			Vận dụng: – So sánh hai số hữu tỉ.
		Các phép toán với số hữu tỉ	Thông hiểu: – Mô tả được phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ và một số tính chất của phép tính đó (tích và thương của hai lũy thừa cùng cơ số, lũy thừa của lũy thừa). – Mô tả được thứ tự thực hiện phép tính, quy tắc dấu ngoặc, quy tắc chuyển vế trong tập hợp số hữu tỉ.		1 (TL1a)
			Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số hữu tỉ. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số hữu tỉ trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về số hữu tỉ (ví dụ: các bài toán liên quan chuyển động trong Vật lí, đo đạc, …).			4 (TL2a, TL2b, TL3a, TL3b)
			Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với các phép tính về số hữu tỉ. – Tính được tổng dãy số có quy luật.				(TL5)
2	Số thực	Số thập phân vô hạn tuần hoàn. Số vô tỉ. Căn bậc hai số học	Nhận biết: – Nhận biết số thập phân hữu hạn và số thập phân vô hạn tuần hoàn. – Nhận biết số vô tỉ. – Nhận biết căn bậc hai số học của một số không âm.	2 (TN5, TN6)
			Thông hiểu: – Mô tả được cách viết chu kì của số thập phân vô hạn tuần hoàn. – Tính giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số nguyên dương bằng máy tính cầm tay – Làm tròn số căn cứ vào độ chính xác cho trước.		1 (TL1b)
		Tập hợp các số thực	Nhận biết: – Nhận biết số thực, số đối và giá trị tuyệt đối của số thực. – Nhận biết thứ tự trong tập hợp các số thực.	2 (TN7, TN8)
			Thông hiểu: – Biểu diễn số thực trên trục số trong trường hợp thuận lợi.
			Vận dụng: – So sánh hai số thực. – Vận dụng các tính chất và quy tắc để thực hiện các phép tính với số thực (tương tự như số hữu tỉ).			2 (TL2c, TL3c)
3	Góc và đường thẳng song song	Góc ở vị trí đặc biệt. Tia phân giác của một góc	Nhận biết: – Nhận biết hai góc kề bù, hai góc đối đỉnh. – Nhận biết tia phân giác của một góc.	2 (TN9, TN10)
			Vận dụng: – Vẽ tia phân giác của một góc bằng dụng cụ học tập. – Tính được số đo góc dựa vào tính chất của các góc ở vị trí đặc biệt. – Tính được số đo góc dựa vào tính chất của tia phân giác.			2 (TL4b, TL4c)
		Dấu hiệu nhận biết và tính chất hai đường thẳng song song. Tiên đề Euclid.	Nhận biết: – Nhận biết các góc tạo bởi một đường thẳng cắt hai đường thẳng. – Nhận biết cách vẽ hai đường thẳng song song. – Nhận biết tiên đề Euclid về đường thẳng song song.	1 (TN11)
			Thông hiểu: – Mô tả dấu hiệu nhận biết hai đường thẳng song song thông qua cặp góc đồng vị, cặp góc so le trong. – Mô tả một số tính chất của hai đường thẳng song song.
			Vận dụng: – Chứng minh hai đường thẳng song song. – Tính số đo của góc tạo bởi hai đường thẳng song song.			1 2 (TL4b, TL4c)
		Định lí và chứng minh định lí	Nhận biết: – Nhận biết một định lí, giả thiết, kết luận của định lí.	3 (TN12, TL4a)
			Vận dụng: – Làm quen với chứng minh định lí.

 

Đề thi Giữa kì 1 Toán lớp 7 có đáp án năm 2023 – Đề 3

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

 

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Tập hợp các số viết được dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ, b ≠ 0 được kí hiệu là:

A. ℕ;

B. ℤ;

C. ℚ;

D. ℝ.

Câu 2. Số đối của số $-\frac{-9}{10}$ là:

A. $\frac{9}{10};$

B. $-\frac{9}{10};$

C. $\frac{10}{9};$

D. $-\frac{10}{9}.$

Câu 3. Cho a = $-\frac{7}{2}$ và b = –4,5. Khẳng định nào sau đây là đúng?

A. a > b;

B. a = b;

C. a < b;

D. a ≤ b.

Câu 4. Số $\frac{2}{3}$ được biểu diễn trên trục số bởi hình vẽ nào dưới đây?

A. 

B. 

C. 

D. 

Câu 5. Số nào sau đây là số thập phân vô hạn không tuần hoàn?

A. –1,23;

B. $\frac{1}{2}$;

C. 3,(45);

D. $\sqrt{2}$.

Câu 6. Chọn khẳng định đúng:

A. Số âm không có căn bậc hai số học;

B. Số âm có hai căn bậc hai số học là hai số đối nhau;

C. Số âm chỉ có một căn bậc hai số học là một số dương;

D. Số âm chỉ có một căn bậc hai số học là một số âm.

Câu 7. Giá trị tuyệt đối của $-\frac{8}{3}$ là:

A. $-\frac{8}{3}$

B. $\frac{8}{3}$;

C. $-\frac{3}{8}$;

D. $\frac{3}{8}.$

Câu 8. Trên trục số nằm ngang, điểm M và N lần lượt biểu biễn hai số thực –0,2 và –3 thì:

A. Điểm M nằm bên trái điểm N;

B. Điểm M nằm bên phải điểm N;

C. Điểm M nằm phía dưới điểm N;

D. Điểm M nằm phía trên điểm N.

Câu 9. Quan sát hình vẽ.

Góc đối đỉnh với $\widehat{\text{AOD}}$ là:

A. $\widehat{\text{DOA}};$

B. $\widehat{\text{BOC}};$

C. $\widehat{\text{AOB}};$

C. $\widehat{\text{DOC}}.$

Câu 10. Tia Oz là tia phân giác của $\widehat{\text{xOy}}$, biết rằng $\widehat{\text{xOz}}=40°$. Số đo của $\widehat{\text{yOz}}$ là:

A. 20°;

B. 40°;

C. 80°;

D. 140°.

Câu 11. Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó?

A. Một đường thẳng;

B. Hai đường thẳng;

C. Không đường thẳng;

D. Vô số đường thẳng.

Câu 12. Trong các câu sau, câu nào không phải định lí?

A. Nếu hai góc bằng nhau thì chúng đối đỉnh;

B. Nếu hai góc kề bù thì tổng số đo của chúng bằng 180°;

C. Nếu hai góc bù nhau thì tổng số đo của chúng bằng 180°;

D. Nếu hai góc đối đỉnh thì chúng bằng nhau.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Viết kết quả của biểu thức ${\left(\frac{1}{16}\right)}^{15}:{\left(0,25\right)}^{28}$ dưới dạng lũy thừa của $\frac{1}{4}$.

b) Cho a = 0,16951695….

i) Số a có phải là số thập phân vô hạn tuần hoàn hay không? Chỉ ra chu kì rồi viết gọn nếu a là số thập phân vô hạn tuần hoàn.

ii) Làm tròn số a với độ chính xác là 0,05.

Bài 2. (1,5 điểm) Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):

a) $\left(\frac{2}{3}-1\right)-\left(\frac{1}{3}-\left(\frac{5}{3}-1\right)\right)$;

b) $\left(\frac{1}{3}+\frac{1}{6}\right).\frac{1}{11}-\frac{1}{2}:\left(1-\frac{1}{12}\right)$;

c) $-\frac{{\left(\sqrt{25}\right)}^2}{13}-\frac{\sqrt{81}}{17}+\frac{12}{13}+\left(-\frac{25}{17}\right).$

Bài 3. (1,5 điểm) Tìm x, biết:

a) $\frac{1}{20}-\left(x-\frac{8}{5}\right)=\frac{1}{10}$;

b) 7,2 : [41 – (2x – 5)] = 2³.5;

c) |5 – 2x| = 4.

Bài 4. (0,5 điểm) Vẽ tia phân giác Oz của $\widehat{xOy}=150°.$

Bài 5. (1,5 điểm) Cho các đường thẳng xx’, yy’, zz’, tt’ cắt nhau như hình vẽ dưới đây:

a) Vẽ lại hình và viết giả thiết, kết luận của bài toán.

b) Chứng minh xx’ // yy’.

c) Tìm số đo a, b.

Bài 6. (0,5 điểm) Trong tiết học môn Toán của lớp Minh, cô giáo đưa ra một câu đố như sau:

Trên một tờ giấy chứa 64 ô vuông, theo thứ tự ô vuông từ trái sang phải rồi từ trên xuống dưới, lần lượt điền các số $\frac{1}{2},\frac{1}{4},\frac{1}{8},\mathrm{\dots .}$ (như hình vẽ) đến khi nào điền kín tất cả các ô vuông. So sánh tổng giá trị của 64 ô vuông đó với số 1.

Em hãy giúp các bạn trong lớp Minh giải câu đố của cô giáo.

ĐÁP ÁN & HƯỚNG DẪN GIẢI

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	C	B	A	A	D	A	B	B	B	B	A	A

Câu 1.

Đáp án đúng là: C

Tập hợp các số viết được dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ, b ≠ 0 là tập hợp số hữu tỉ, được kí hiệu là ℚ.

Câu 2.

Đáp án đúng là: B

Ta có: $-\frac{-9}{10}=\frac{9}{10}$

Số đối của số $-\frac{-9}{10}=\frac{9}{10}$ là $-\frac{9}{10}.$

Câu 3.

Đáp án đúng là: A

Ta có a = $-\frac{7}{2}$ = –3,5 > –4,5.

Do đó a > b.

Câu 4.

Đáp án đúng là: A

Biểu diễn số $\frac{2}{3}$ trên trục số ta làm như sau:

• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 3 phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng $\frac{2}{3}$ đơn vị cũ.

• Số $\frac{2}{3}$ được biểu diễn bởi điểmnằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới.

Ta chọn phương án A.

Câu 5.

Đáp án đúng là: D

Các số –1,23 và $\frac{1}{2}=0,5$ là số thập phân hữu hạn.

Số 3,(45) là số thập phân vô hạn tuần hoàn.

Số $\sqrt{2}$ là số thập phân vô hạn không tuần hoàn hay còn gọi là số vô tỉ.

Câu 6.

Đáp án đúng là: A

Số âm không có căn bậc hai số học.

Ta chọn phương án A.

Câu 7.

Đáp án đúng là: B

Vì $–\frac{8}{3}$ < 0 nên  = –$\left(–\frac{8}{3}\right)=\frac{8}{3}$

Vậy giá trị tuyệt đối của $-\frac{8}{3}$ là $\frac{8}{3}.$

Câu 8.

Đáp án đúng là: B.

Trên trục số nằm ngang, điểm M và N lần lượt biểu biễn hai số thực –0,2 và –3.

Ta có –0,2 > –3 nên điểm M nằm bên phải điểm N.

Câu 9.

Đáp án đúng là: B

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Ta có OC là tia đối của tia OA; OB là tia đối của OD do đó góc đối đỉnh với $\widehat{\text{AOD}}$ là $\widehat{\text{BOC}}$ nên B đúng.

Câu 10.

Đáp án đúng là: B

Theo bài ta có: Oz là tia phân giác của $\widehat{\text{xOy}}$

Nên $\widehat{\text{xOz}}=\widehat{\text{zOy}}$ (tính chất tia phân giác của một góc).

Mà $\widehat{\text{xOz}}=40°$

Suy ra $\widehat{\text{yOz}}=40°$

Vậy ta chọn phương án B.

Câu 11.

Đáp án đúng là: A

Theo tiên đề Euclid ta có: qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Câu 12.

Đáp án đúng là: A

Hai góc bù nhau là hai góc có tổng số đo bằng 180° nên C đúng.

Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau mà hai góc bù nhau là hai góc có tổng số đo bằng 180° nên B đúng.

Hai góc đối đỉnh thì bằng nhau nên D đúng.

Hai góc bằng nhau chưa chắc đã đối đỉnh nên khẳng định này sai.

Chẳng hạn:

Ví dụ: $\widehat{\text{xOy}}=\widehat{\text{yOz}}$ (cùng bằng 25°) nhưng $\widehat{\text{xOy}},\widehat{\text{yOz}}$ là hai góc kề nhau, không phải là hai góc đối đỉnh.

Do đó phương án A không phải là một định lí nên A sai.

Vậy ta chọn phương án A.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Ta thấy $0,25=\frac{1}{4}$ và $\frac{1}{16}=\frac{1^2}{4^2}={\left(\frac{1}{4}\right)}^2$.

Do đó ta sẽ biến đổi biểu thức đã cho dưới dạng các lũy thừa có cùng cơ số $\frac{1}{4}$ như sau:

Ta có ${\left(\frac{1}{16}\right)}^{15}:{\left(0,25\right)}^{28}$

$={\left({\left(\frac{1}{4}\right)}^2\right)}^{15}:{\left(\frac{1}{4}\right)}^{28}={\left(\frac{1}{4}\right)}^{2.15}:{\left(\frac{1}{4}\right)}^{28}$

$={\left(\frac{1}{4}\right)}^{30}:{\left(\frac{1}{4}\right)}^{28}={\left(\frac{1}{4}\right)}^{30-28}={\left(\frac{1}{4}\right)}^2.$

b) Số a = 0,16951695….

i) Số a là số thập phân vô hạn tuần hoàn với chu kì là 1695, viết gọn là a = 0,(1695).

ii) Làm tròn số a = 0,16951695…. với độ chính xác là 0,05 tức là ta làm tròn số đến hàng phần mười, được kết quả là 0,2.

Bài 2. (1,5 điểm)

a) $\left(\frac{2}{3}-1\right)-\left(\frac{1}{3}-\left(\frac{5}{3}-1\right)\right)$

$=\frac{2}{3}-1-\left(\frac{1}{3}-\frac{5}{3}+1\right)$

$=\frac{2}{3}-1-\frac{1}{3}+\frac{5}{3}-1$

$=\left(\frac{2}{3}-\frac{1}{3}+\frac{5}{3}\right)+\left(-1-1\right)$

$=\frac{6}{3}-2=2-2=0.$

b) $\left(\frac{1}{3}+\frac{1}{6}\right).\frac{1}{11}-\frac{1}{2}:\left(1-\frac{1}{12}\right)$

$=\left(\frac{2}{6}+\frac{1}{6}\right).\frac{1}{11}-\frac{1}{2}:\left(\frac{12}{12}-\frac{1}{12}\right)$

$=\frac{3}{6}.\frac{1}{11}-\frac{1}{2}:\frac{11}{12}=\frac{1}{2}.\frac{1}{11}-\frac{1}{2}.\frac{12}{11}$

$=\frac{1}{2}.\left(\frac{1}{11}-\frac{12}{11}\right)=\frac{1}{2}.\frac{-11}{11}=-\frac{1}{2}$.

c) $-\frac{{\left(\sqrt{25}\right)}^2}{13}-\frac{\sqrt{81}}{17}+\frac{12}{13}+\left(-\frac{25}{17}\right)$

$=-\frac{25}{13}-\frac{9}{17}+\frac{12}{13}+\left(-\frac{25}{17}\right)$

$=\left(-\frac{25}{13}+\frac{12}{13}\right)+\left(-\frac{9}{17}-\frac{25}{17}\right)$

$=\frac{-13}{13}+\frac{-34}{17}=\left(-1\right)+\left(-2\right)=-3.$

Bài 3. (1,5 điểm) Tìm x, biết:

a) $\frac{1}{20}-\left(x-\frac{8}{5}\right)=\frac{1}{10}$

$x-\frac{8}{5}=\frac{1}{20}-\frac{1}{10}$

$x-\frac{8}{5}=\frac{1}{20}-\frac{2}{20}$

$x-\frac{8}{5}=-\frac{1}{20}$

$x=-\frac{1}{20}+\frac{8}{5}$

$x=-\frac{1}{20}+\frac{32}{20}$

$x=\frac{31}{20}$

Vậy $x=\frac{31}{20}$.

b) 7,2 : [41 – (2x – 5)] = 2³ . 5.

7,2 : [41 – (2x – 5)] = 8 . 5

7,2 : [41 – (2x – 5)] = 40

41 – (2x – 5) = 7,2 : 40

41 – (2x – 5) = 0,18

2x – 5 = 41 – 0,18

2x – 5 = 40,82

2x = 40,82 + 5

2x = 45,82

x = 45,82 : 2

x = 22,91

Vậy x = 22,91.

c) |5 – 2x| = 4

Trường hợp 1: 5 – 2x = 4

2x = 5 – 4

2x = 1

$x=\frac{1}{2}$

Trường hợp 2: 5 – 2x = –4

2x = 5 – (–4)

2x = 5 + 4

2x = 9

$x=\frac{9}{2}$

Vậy có hai giá trị của x là $x=\frac{1}{2}$; $x=\frac{9}{2}$.

Bài 4. (0,5 điểm)

Nếu Oz là tia phân giác của góc xOy thì $\widehat{xOz}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}.150°=75°.$

Ta sử dụng thước đo góc vẽ theo các bước sau:

Bài 5. (1,5 điểm)

a) Học sinh vẽ lại hình.

Viết giả thiết, kết luận:

b) Ta có $\widehat{x^{‘}A{z}^{‘}}$ và $\widehat{zA{x}^{‘}}$ là hai góc kề bù nên $\widehat{x^{‘}A{z}^{‘}}+\widehat{zA{x}^{‘}}=180°$.

Suy ra $\widehat{zA{x}^{‘}}=180°-\widehat{x^{‘}A{z}^{‘}}=180°-105°=75°$

Do đó $\widehat{x^{‘}A{z}^{‘}}=\widehat{zB{z}^{‘}}$ (cùng bằng 75°).

Mà $\widehat{x^{‘}A{z}^{‘}}$ và $\widehat{zB{z}^{‘}}$ là hai góc ở vị trí đồng vị.

Suy ra xx’ // yy’ (dấu hiệu nhận biết hai đường thẳng song song).

Vậy xx’ // yy’.

c) Vì xx’ // yy’ (theo câu a) nên $\widehat{x^{‘}C{t}^{‘}}=\widehat{tDy}=70°$ (hai góc so le trong).

Do đó a = 70°.

Ta có xx’ // yy’ và mn ⊥ xx’ nên mn ⊥ yy’ (một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia).

Do đó $\widehat{mDy}=90°.$

Lại có $\widehat{tDy}+\widehat{tDm}=\widehat{mDy}$ (hai góc kề nhau).

Suy ra $\widehat{tDm}=\widehat{mDy}-\widehat{tDy}=90°-70°=20°.$

Do đó b = 20°.

Vậy a = 70° và b = 20°.

Bài 6. (0,5 điểm)

Ta đặt tên cho giá trị của các ô vuông lần là A₁, A₂, A₃, …, A₆₄ (hình vẽ).

Ta thấy: $A_1=\frac{1}{2};$

$A_2=\frac{1}{4}=\frac{1}{2^2};$

$A_2=\frac{1}{8}=\frac{1}{2^3};$

….

Do đó: $A_{63}=\frac{1}{2^{63}}$; $A_{64}=\frac{1}{2^{64}}$

Khi đó: A = A₁ + A₂ + A₃ + … + A₆₃ + A₆₄

Hay $A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\mathrm{\dots }+\frac{1}{2^{63}}+\frac{1}{2^{64}}$

Suy ra $2A=2.\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\mathrm{\dots }+\frac{1}{2^{63}}+\frac{1}{2^{64}}\right)$

$2A=\frac{2}{2}+\frac{2}{2^2}+\frac{2}{2^3}+\mathrm{\dots }+\frac{2}{2^{63}}+\frac{2}{2^{64}}$

$2A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\mathrm{\dots }+\frac{1}{2^{63}}$

$2A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\mathrm{\dots }+\frac{1}{2^{63}}+\frac{1}{2^{64}}-\frac{1}{2^{64}}$

$2A=1+\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\mathrm{\dots }+\frac{1}{2^{63}}+\frac{1}{2^{64}}\right)-\frac{1}{2^{64}}$

$2A=1+A-\frac{1}{2^{64}}$

Do đó $2A-A=1-\frac{1}{2^{64}}$

Suy ra $A=1-\frac{1}{2^{64}}<1.$

Vậy tổng giá trị của 64 ô vuông nhỏ hơn 1.

A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ 1

STT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ kiến thức, kĩ năng cần kiềm tra, đánh giá								Tổng điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
			TN	TL	TN	TL	TN	TL	TN	TL
1	Số hữu tỉ (14 tiết)	Tập hợp các số hữu tỉ. Thứ tự thực hiện các phép tính.	3 (0,5đ)		1 (0,25đ)						4
		Các phép toán với số hữu tỉ				1 (0,5đ)		4 (2 đ)		1 (0,5đ)
2	Số thực (10 tiết)	Số thập phân vô hạn tuần hoàn. Số vô tỉ. Căn bậc hai số học	2 (0,5đ)			1 (1đ)					3
		Tập hợp các số thực	2 (0,5đ)					2 (1 đ)
3	Góc và đường thẳng song song (11 tiết)	Góc ở vị trí đặc biệt. Tia phân giác của một góc	2 (0,5đ)					1 (0,5đ)			3
		Dấu hiệu nhận biết và tính chất hai đường thẳng song song. Tiên đề Euclid.	1 (0,25đ)					2 (1 đ)
		Định lí và chứng minh định lí	1 (0,25đ)	1 (0,5đ)
Tổng: Số câu Điểm			11 (2,75đ)	1 (0,5đ)	1 (0,25đ)	2 (1,5đ)	0 (0 đ)	9 (4,5đ)	0 (0 đ)	1 (0,5đ)	10
Tỉ lệ			32,5%		1,75%		45%		5%
Tỉ lệ chung			50%				50%

 

B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1

STT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ kiến thức, kĩ năng cần kiềm tra, đánh giá	Số câu hỏi theo mức độ
				Nhận biết	Thông hiểu	Vận dụng	Vận dụng cao
1	Số hữu tỉ	Tập hợp các số hữu tỉ. Thứ tự thực hiện các phép tính.	Nhận biết: – Nhận biết được số hữu tỉ. – Nhận biết được tập hợp các số hữu tỉ ℚ. – Nhận biết được số đối của số hữu tỉ. – Nhận biết được thứ tự trong tập hợp số hữu tỉ.	3 (TN1,TN2, TN3)
			Thông hiểu: – Biểu diễn số hữu tỉ trên trục số.	1 (TN4)
			Vận dụng: – So sánh hai số hữu tỉ.
		Các phép toán với số hữu tỉ	Thông hiểu: – Mô tả được phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ và một số tính chất của phép tính đó (tích và thương của hai lũy thừa cùng cơ số, lũy thừa của lũy thừa). – Mô tả được thứ tự thực hiện phép tính, quy tắc dấu ngoặc, quy tắc chuyển vế trong tập hợp số hữu tỉ.		1 (TL1a)
			Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số hữu tỉ. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số hữu tỉ trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về số hữu tỉ (ví dụ: các bài toán liên quan chuyển động trong Vật lí, đo đạc, …).			4 (TL2a, TL2b, TL3a, TL3b)
			Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với các phép tính về số hữu tỉ. – Tính được tổng dãy số có quy luật.				(TL6)
2	Số thực	Số thập phân vô hạn tuần hoàn. Số vô tỉ. Căn bậc hai số học	Nhận biết: – Nhận biết số thập phân hữu hạn và số thập phân vô hạn tuần hoàn. – Nhận biết số vô tỉ. – Nhận biết căn bậc hai số học của một số không âm.	2 (TN5, TN6)
			Thông hiểu: – Mô tả được cách viết chu kì của số thập phân vô hạn tuần hoàn. – Tính giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số nguyên dương bằng máy tính cầm tay – Làm tròn số căn cứ vào độ chính xác cho trước.		1 (TL1b)
		Tập hợp các số thực	Nhận biết: – Nhận biết số thực, số đối và giá trị tuyệt đối của số thực. – Nhận biết thứ tự trong tập hợp các số thực.	2 (TN7, TN8)
			Thông hiểu: – Biểu diễn số thực trên trục số trong trường hợp thuận lợi.
			Vận dụng: – So sánh hai số thực. – Vận dụng các tính chất và quy tắc để thực hiện các phép tính với số thực (tương tự như số hữu tỉ).			2 (TL2c, TL3c)
3	Góc và đường thẳng song song	Góc ở vị trí đặc biệt. Tia phân giác của một góc	Nhận biết: – Nhận biết hai góc kề bù, hai góc đối đỉnh. – Nhận biết tia phân giác của một góc.	2 (TN9, TN10)
			Vận dụng: – Vẽ tia phân giác của một góc bằng dụng cụ học tập. – Tính được số đo góc dựa vào tính chất của các góc ở vị trí đặc biệt. – Tính được số đo góc dựa vào tính chất của tia phân giác.			1 (TL4)
		Dấu hiệu nhận biết và tính chất hai đường thẳng song song. Tiên đề Euclid.	Nhận biết: – Nhận biết các góc tạo bởi một đường thẳng cắt hai đường thẳng. – Nhận biết cách vẽ hai đường thẳng song song. – Nhận biết tiên đề Euclid về đường thẳng song song.	1 (TN11)
			Thông hiểu: – Mô tả dấu hiệu nhận biết hai đường thẳng song song thông qua cặp góc đồng vị, cặp góc so le trong. – Mô tả một số tính chất của hai đường thẳng song song.
			Vận dụng: – Chứng minh hai đường thẳng song song. – Tính số đo của góc tạo bởi hai đường thẳng song song.			2 (TL5b, TL5c)
		Định lí và chứng minh định lí	Nhận biết: – Nhận biết một định lí, giả thiết, kết luận của định lí.	3 (TN12, TL5a)
			Vận dụng: – Làm quen với chứng minh định lí.

Đề thi Giữa kì 1 Toán lớp 7 có đáp án năm 2023 – Đề 4

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 4)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Câu 1. Số nào dưới đây không phải là số hữu tỉ ?

A. $\frac{3}{0}$;

B. 2;

C. 0,5;

D. $4\frac{5}{7}$.

Câu 2. Chọn khẳng định đúng:

A. Số 0 không có số đối;

B. Mọi số hữu tỉ đều có một số đối;

C. Số đối của số hữu tỉ $\frac{\text{a}}{\text{b}}$ là số hữu tỉ $\frac{\text{b}}{\text{a}}$;

D. Tất cả đều đúng.

Câu 3. Số hữu tỉ nào sau đây nằm giữa $-\frac{\text{2}}{\text{3}}$ và$\frac{1}{6}$ trên trục số?

A. $-\frac{\text{1}}{\text{6}}$;

B. $\frac{1}{3}$;

C. $\frac{-\text{4}}{\text{3}}$;

D. $\frac{2}{3}$.

Câu 4. Giá trị của biểu thức $8.{\left(2^3\right)}^4$ là

A. $2^{14}$;

B. $2^{10}$;

C. $2^{15}$;

D. $2^{13}$.

Câu 5. Số 0,(29) bằng số nào dưới đây?

A. 0,2

B. 0,92

C. 0,2(92)

D. 0,2(29)

Câu 6. Tính $\sqrt{25-9}$ bằng

A. 4;

B. 3;

C. 1;

D. 5.

Câu 7. Giá trị của |−25 + 11.3| − |−2| là

A. −25

B. 25

C. 6

D. −6

Câu 8. Cho A = 3 và B = $\sqrt{12}$. Mệnh đề nào đúng?

A. A > B;

B. A < B;

C. A = B;

D. A ≤ B.

Câu 9. Cho các khẳng định sau:

(I) Hai góc đối đỉnh thì bằng nhau.

(II) Hai góc bằng nhau thì đối đỉnh.

(III) Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.

Số khẳng định đúng là:

A. 0;

B. 1;

C. 2;

D. 3.

Câu 10. Xét bài toán: “Cho $\widehat{aOc}=140°$. Nêu cách dựng tia phân giác của $\widehat{aOc}$ bằng thước đo góc”. Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.

(I) Tính $\frac{\widehat{aOc}}{2}=\frac{140°}{2}=70°$.

(II) Dùng thước nối từ đỉnh của góc tới điểm đã đánh dấu ta được tia phân giác.

(III) Đặt tâm của thước đo góc trùng với đỉnh O sao cho một cạnh của thước đo trùng với cạnh Oc.

(IV)Dựng góc $\widehat{aOc}=140°$.

(V) Đánh dấu điểm chỉ vạch 70°.

Sắp xếp nào sau đây đúng?

A. (III) – (V) – (I) – (II) – (IV);

B. (III) – (I) – (V) – (II) – (IV);

C. (IV) – (III) – (I) – (V) – (II);

D. (IV) – (III) – (I) – (II) – (V).

Câu 11. Cho hình vuông ABCD. Vẽ đường thẳng a đi qua B và song song với AC. Vẽ được bao nhiêu đường thẳng a?

A. 0;

B. 1;

C. 2;

D. Vô số.

Câu 12. Một định lí được minh họa bởi hình vẽ:

Định lí có giả thiết và kết luận như sau:

Định lí được phát biểu thành lời là:

A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc bất kì bằng nhau;

B. Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau nhau thì hai đường thẳng đó song song;

C. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau;

D. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có tổng bằng 180°.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm)Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):

a) $\frac{39}{5}+\left(\frac{9}{4}-\frac{9}{5}\right)-\left(\frac{5}{4}+\frac{6}{7}\right)$;

b) ${\left(\frac{-1}{7}\right)}^5.{(-7)}^5-{2022}^0$;

c) $\frac{1}{2023}.\frac{-6}{7}+\frac{2022}{2023}.\frac{-6}{7}+\frac{6}{7}$;

d) $3.\sqrt{\frac{1}{9}}+3.{\left(\sqrt{0,01}\right)}^2$.

Bài 2. (1,5 điểm)Tìm x, biết:

a) $\left(\frac{3}{2}-x\right):\frac{-14}{3}=\frac{-6}{7}$;

b) ${182}^{\text{x}}{\text{: 13}}^{\text{x}}\text{= 196;}$

c) |x-$\sqrt{25}$| = 0

Bài 3. (1,0 điểm)Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Biết kích thước màn hình của một chiếc ti vi bằng độ dài đường chéo màn hình (tính theo inch, 1 inch ≈ ≈ 2,54 cm).

Màn hình của một chiếc tivi có chiều dài là 70 cm, chiều rộng là 41 cm. Hãy tính kích thước màn hình của chiếc ti vi đó (làm tròn kết quả đối với đơn vị cm với độ chính xác 0,05 và đối với đơn vị inch làm tròn đến hàng đơn vị).

Bài 4. (2,0 điểm)Cho ba điểm A, B, C sao cho $\widehat{ABC}=70°.$ Vẽ tia phân giác Bx của $\widehat{ABC},$ cắt AC tại F. Trên cạnh AB lấy điểm E sao cho $\widehat{BFE}=35°.$

a) Vẽ hình và viết giả thiết, kết luận của bài toán.

b) Chứng minh EF // BC.

c) Tính số đo của góc BEF.

d) Vẽ tia Ey là tia phân giác của góc BEF. Chứng minh BF ⊥ Ey.

Bài 4. (0,5 điểm)Tìm x biết: $\frac{1}{14}+\frac{1}{35}+\frac{1}{65}+\mathrm{..}+\frac{2}{{\text{x}}^2+3\text{x}}=\frac{1}{9}$.

Đề thi Giữa kì 1 Toán lớp 7 có đáp án năm 2023 – Đề 5

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán lớp 7

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 5)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Câu 1. Chọn đáp án đúng

A. ℝ ⊂ ℤ;

B. ℝ ⊂ ℕ;

C. ℚ ⊂ ℤ;

D. ℤ ⊂ ℚ.

Câu 2. Chọn khẳng định sai:

A. Số đối của số –3,5 có giá trị là 3,5;

B. Số đối của số –3,5 có giá trị là $\frac{7}{2};$

C. Số đối của số –3,5 có giá trị là $\frac{7}{2};$

D. Số đối của số –3,5 có giá trị là 3$\frac{1}{2}.$

Câu 3. Nhiệt độ nóng chảy của một số kim loại được cho trong bảng:

Tên kim loại	Sắt (Fe)	Thuỷ ngân (Hg)	Magie (Mg)	Natri (Na)	Wolfram (W)
Nhiệt độ nóng chảy (℃)	1538	–38,83	650	97,72	3410

Sắp xếp các kim loại trên theo nhiệt độ nóng chảy tăng dần là

A. Na; Hg; Mg; Fe; W;

B. Fe; Na; Hg; Mg; W;

C. Hg; Mg; Fe; Na; W;

D. Hg; Na; Mg; Fe; W.

Câu 4. Trong các điểm M, N, P được biểu diễn trên trục số thì điểm nào biểu diễn số hữu tỉ âm?

A. Điểm M;

B. Điểm N;

C. Điểm P;

D. Điểm O.

Câu 5. Trong các số sau đây số nào là số vô tỉ:

A. 0,23;

B. 1,234567…;

C. 1,33333…;

D. $\frac{1}{2}$.

Câu 6. $\sqrt{{(-3)}^2}$ bằng:

A. 3;

B. –3;

C. 9;

D. –9.

Câu 7. Số có giá trị tuyệt đối nhỏ nhất trong các số $\sqrt{2}$; $-\sqrt{3}$; 2; -3 là:

A. $\sqrt{2}$;

B. $-\sqrt{3}$;

C. 2;

D. −3.

Câu 8. Kết quả của phép tính ${(-0,2)}^{10}.\frac{1}{-5}$ với $a=\frac{-1}{5}$ được viết dưới dạng lũy thừa của a là:

A. a⁸;

B. a⁹;

C. a¹⁰;

D. a¹¹.

Câu 9. Cho hình vẽ sau, khẳng định nào sau đây sai?

A. $\widehat{xBy}$ và $\widehat{yBz}$ là hai góc kề nhau;

B. $\widehat{xBy}$ và $\widehat{yBz}$ là hai góc bù nhau;

C. $\widehat{xBy}$ và $\widehat{yBz}$ là hai góc kề bù;

D. $\widehat{xBy}$ và $\widehat{yBz}$ là hai góc đối đỉnh.

Câu 10.Tia Ob là phân giác của $\widehat{aOc}$ trong hình vẽ nào dưới đây?

A. 

B. 

C. 

D. 

Câu 11. Cho ba điểm A, B, C. Qua đỉnh A vẽ đường thẳng a song song với BC. Qua đỉnh C vẽ đường thẳng b song song với AB. Hỏi vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b?

A. 1 đường thẳng a, 1 đường thẳng b;

B.1 đường thẳng a, 2 đường thẳng b;

C.2 đường thẳng a, 1 đường thẳng b;

D.2 đường thẳng a, 2 đường thẳng b.

Câu 12. Cho định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì chúng song song với nhau” (hình vẽ). Giả thiết của định lí là

A. a // b;

B. a ⊥ c;

C. b ⊥ c;

D. Cả B và C.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm)Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):

a) $\frac{17}{11}-\left(\frac{6}{5}-\frac{16}{11}\right)+\frac{26}{5}$;

b) $\left(7-\frac{1}{2}-\frac{5}{4}\right):\left(5-\frac{2}{3}-\frac{1}{6}\right)$;

c) $\frac{{\left(0,2\right)}^5.0,3^3}{{\left(0,2\right)}^7.{\left(0,3\right)}^4};$

d) $\left(\frac{2}{7}.\frac{3}{5}+\frac{2}{5}.\frac{4}{7}\right)$ +  : $\frac{4}{3}$

Bài 2. (1,5 điểm)Tìm x, biết:

a) $x+\frac{1}{2}=-\frac{6}{7}$;

b) |x + 25| = 0;

c) ${\left(x-\frac{1}{2}\right)}^2=\frac{1}{16}$.

Bài 3. (1,0 điểm)Một khu vườn hình vuông có diện tích 200 m². Tính độ dài mỗi cạnh của khu vườn với độ chính xác 0,005.

Bài 4. (2,0 điểm)Cho hình vẽ sau:

Biết b // c và $\widehat{\text{dAa}}=\widehat{dBb}=60°.$

a) Viết giả thiết và kết luận của bài toán.

b) Tính số đo góc C₁.

b) Chứng minh a // c.

Bài 4. (0,5 điểm)Tính giá trị của biểu thức:

$A=-\frac{1}{3}+\frac{1}{3^2}-\frac{1}{3^3}+\frac{1}{3^4}-\mathrm{\dots }+\frac{1}{3^{50}}-\frac{1}{3^{51}}$