Giải bài tập Toán lớp 7 Luyện tập chung trang 50
Video bài giảng Luyện tập chung trang 50 – Kết nối tri thức
Bài 3.12 trang 50 Toán lớp 7: Cho Hình 3.28.
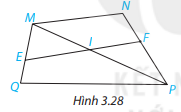
a) Tìm các góc ở vị trí so le trong với góc FIP; góc NMI
b) Tìm các góc ở vị trí đồng vị với góc EQP; góc IFP.
Phương pháp giải:
Nhận diện cặp góc so le trong, đồng vị
Lời giải:
a) Góc ở vị trí so le trong với góc FIP là góc IPQ
Góc ở vị trí so le trong với góc NMI là góc MIE và góc MPQ.
b) Góc ở vị trí đồng vị với góc EQP là góc MEF
Góc ở vị trí đồng vị với góc IFP là góc MNF
Bài 3.13 trang 50 Toán lớp 7: Cho Hình 3.29, biết , . Giải thích tại sao Ax//By.
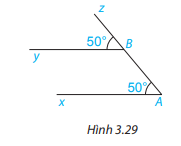
Phương pháp giải:
Sử dụng Dấu hiệu nhận biết hai đường thẳng song song
Lời giải:
Vì , mà hai góc này ở vị trí đồng vị nên Ax//By (Dấu hiệu nhận biết hai đường thẳng song song)
Bài 3.14 trang 50 Toán lớp 7: Vẽ hình theo yêu cầu sau:
a) Vẽ hai đường thẳng d và d’ sao cho d // d’.
b) Vẽ hai đoạn thẳng AB và CD sao cho CD = 2AB và CD //AB
Phương pháp giải:
Vẽ 2 đường thẳng song song
Lời giải:
a) Vẽ đường thẳng d
Vẽ đường thẳng d’ song song với d
b) Vẽ đoạn thẳng CD. Đo độ dài CD.
Kẻ đường thẳng a // CD
Trên đường thẳng a, lấy 2 điểm A và B sao cho AB = CD : 2

Chú ý:
Để dễ dàng vẽ 2 đường thẳng song song, ta có thể kẻ các đường thẳng trùng với dòng kẻ của quyển vở.
Bài 3.15 trang 50 Toán lớp 7: Cho Hình 3.30, biết các góc MNQ và PQN có cùng số đo bằng 35. Chứng tỏ MN//QP.
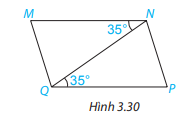
Phương pháp giải:
Sử dụng Dấu hiệu nhận biết hai đường thẳng song song
Lời giải:
Vì , mà hai góc này ở vị trí so le trong nên MN // QP. (Dấu hiệu nhận biết hai đường thẳng song song)
Bài 3.16 trang 50 Toán lớp 7: Cho đoạn thẳng AB. Vẽ hai tia Ax, By sao cho chúng tạo với AB hai góc so le trong có cùng số đo bằng 60(). Trên hình vừa vẽ, hai đường thẳng chứa hai tia Ax và By có song song với nhau không? Vì sao?
Phương pháp giải:
Vẽ hình.
Sử dụng Dấu hiệu nhận biết hai đường thẳng song song
Lời giải:
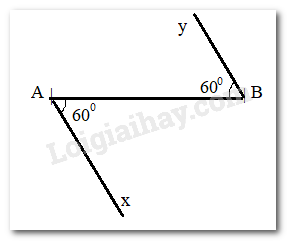
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì , mà hai góc này ở vị trí so le trong nên Ax // By.
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 11: Định lí và chứng minh định lí
Luyện tập chung trang 58