20 Bài tập Làm quen với số thập phân vô hạn tuần hoàn có đáp án – Toán 7

Bài tập Toán lớp 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn

A. Bài tập Làm quen với số thập phân vô hạn tuần hoàn

A1. Bài tập tự luận

Bài 1. Trong các số thập phân sau, số nào là số thập phân hữu hạn? Số nào là số thập phân vô hạn tuần hoàn?

a) 0,134;

b) 0,12878787…;

c) – 5,(6);

d) 1,15;

e) 5,3(12)

f) 0,30300300030000… (viết liên tiếp các số 30; 300; 3000; 30 000; … sau dấu phẩy).

Hướng dẫn giải

a) 0,134 là số thập phân hữu hạn.

b) 0,12878787… = 0,12(87) có số 87 ở phần thập phân được lặp lại mãi nên 0,12878787… là số thập phân vô hạn tuần hoàn.

c) – 5,(6) có số 6 ở phần thập phân được lặp lại mãi nên – 5,(6) là số thập phân vô hạn tuần hoàn.

d) 1,15 là số thập phân hữu hạn.

e) 5,3(12) có số 12 ở phần thập phân được lặp lại mãi nên 5,3(12) là số thập phân vô hạn tuần hoàn.

f) 0,30300300030000… (viết liên tiếp các số 30; 300; 3000; 30 000; … sau dấu phẩy) không là số thập phân hữu hạn, cũng không là số thập phân vô hạn tuần hoàn vì phần thập phân không được lặp lại đều đặn.

Bài 2. Làm tròn các số 192,25202; 12,(81); 32,(503).

a) Đến chữ số thập phân thứ ba;

b) Với độ chính xác là 5.

Hướng dẫn giải

a) +) Số 192,25202 có chữ số sau chữ số thập phân thứ ba là 0 < 5 nên ta giữ nguyên chữ số hàng làm tròn. Do đó ta có: 192,25202 ≈ 192,252.

+) Số 12,(81) = 12,818181… có chữ số sau chữ số thập phân thứ ba là 1 < 5 nên ta giữ nguyên chữ số hàng làm tròn. Do đó ta có: 12,818181… ≈12,818 hay 12,(81) ≈12,818.

+) Số 32,(503) = 32,503503… có chữ số sau chữ số thập phân thứ ba là 5 = 5 nên ta cộng 1 đơn vị vào chữ số hàng làm tròn. Do đó ta có: 32,503503… ≈ 32,504 hay 32,(503) ≈ 32,504.

b) Với độ chính xác là 5 tức là làm tròn đến hàng phần chục

Số 192,25202 có chữ số sau hàng chục là 2 < 5 nên 192,25202 ≈ 190.

Số 12,(81) = 12,818181… có chữ số sau hàng chục là 2 < 5 nên 12,(81) ≈ 10.

Số 32,(503) = 32,503503… có chữ số sau hàng chục là 3 < 5 nên  32,(503) ≈ 30.

Bài 3. Sử dụng chu kì, hãy viết gọn các số thập phân vô hạn tuần hoàn dưới đây:

a) 0,010101…

b) – 0,13888…

c) 5,3022121…

d) 0,1636363…

Hướng dẫn giải

a) Ta thấy số 0,010101… phần thập phân có chu kỳ là 01 nên 0,010101… = 0,(01)

b) Ta thấy số – 0,13888…  phần thập phân có chu kỳ là 8 nên – 0,13888… = – 0,13(8)

c) Ta thấy số 5,3022121… phần thập phân có chu kỳ là 21 nên 5,3022121… = 5,302(21)

d) Ta thấy số 0,1636363… phần thập phân có chu kỳ là 63 nên 0,1636363… = 0,1(63)

A2. Bài tập trắc nghiệm

Bài 4. Nhìn thật nhanh xem đâu là số thập phân vô hạn tuần hoàn?

A. $\frac{2}{3}$;

B. $\frac{3}{4}$;

C. $\frac{2}{5}$;

D. $\frac{7}{20}$.

Hướng dẫn giải

Đáp án đúng là: A

Người ta đã chứng minh được rằng:

– Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

– Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

$\frac{2}{3}$ có mẫu số là 3 và mẫu số có ước nguyên tố khác 2 và 5 nên phân số $\frac{2}{3}$ được viết dưới dạng số thập phân vô hạn tuần hoàn.

$\frac{3}{4}$ có mẫu số là 4 và mẫu số chỉ có ước nguyên tố là 2 nên phân số $\frac{3}{4}$ được viết dưới dạng số thập phân hữu hạn.

$\frac{2}{5}$ có mẫu số là 5 và mẫu số chỉ có ước nguyên tố là 5 nên phân số $\frac{2}{5}$ được viết dưới dạng số thập phân hữu hạn.

$\frac{7}{20}=\frac{7}{4\times 5}=\frac{7}{2\times 2\times 5}$ có mẫu số là 20 và mẫu số chỉ có ước nguyên tố là 2 và 5 nên phân số $\frac{7}{20}$ được viết dưới dạng số thập phân hữu hạn.

Bài 5. Khi viết phân số $\frac{3}{11}$ thành số thập phân và làm tròn với độ chính xác là 0,005 thì ta được kết quả là?

A. 0,27;

B. 0,(27);

C. 0,2(72);

D. 0,273.

Hướng dẫn giải

Đáp án đúng là: A

Độ chính xác 0,005 là làm tròn đến phần trăm.

Ta có: $\frac{3}{11}$ = 0,272727…

Ta gạch chân dưới chữ số hàng phần trăm 0,272727272… Nhận thấy chữ số hàng phần nghìn là 2 < 5 nên ta giữ nguyên chữ số hàng phần trăm và bỏ đi các chữ số thập phân sau hàng phần trăm.

$\frac{3}{11}$= 0,272727272… $\approx$0,27.

Bài 6. Đâu là số thập phân vô hạn tuần hoàn?

A. 3,243564…;

B. 3,101001000…;

C. 5,31241212…;

D. 7,2132123….

Hướng dẫn giải

Đáp án đúng là: C

3,243564… có phần thập phân không tuần hoàn nên 3,243564… không phải số thập phân vô hạn tuần hoàn.

3,101001000… có phần thập phân không tuần hoàn nên 3,101001000… không phải số thập phân vô hạn tuần hoàn.

5,31241212… = 5,3124(12) là số thập phân vô hạn tuần hoàn.

7,2132123… có phần thập phân không tuần hoàn nên 7,2132123… không phải số thập phân vô hạn tuần hoàn.

B. Lý thuyết Làm quen với số thập phân vô hạn tuần hoàn

1. Số thập phân vô hạn tuần hoàn

• Số thập phân vô hạn tuần hoàn là biểu diễn thập phân của một số có phần thập phân lặp lại (lặp lại giá trị của nó ở các khoảng đều đặn) và phần lặp lại vô hạn không phải là số không.

• Chu kì của số thập phân vô hạn tuần hoàn là phần được lặp lại vô hạn lần.

• Số thập phân hữu hạn là số thập phân như 0,34; 1,2; 6,7; …

Ví dụ:

+ Khi chia 7 cho 3 được thương là 2,333…, chữ số 3 được lặp lại mãi. Nên $\frac{7}{3}=2,333\dots =2,\left(3\right)$ là số thập phân vô hạn tuần hoàn với chu kì là 3.

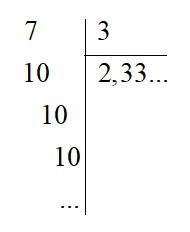
+ Phân số $\frac{19}{11}=1,\mathrm{727272\dots }=1,\left(72\right)$ là số thập phân vô hạn tuần hoàn với chu kì là 72.

+ Phân số $-\frac{1009}{900}=-1,\mathrm{12111\dots }=-1,21\left(1\right)$ là số thập phân vô hạn tuần hoàn với chu kì là 1.

Chú ý:

• Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ:  Số $\frac{12}{5}=2,4$;  $-\frac{1}{15}=-0,\mathrm{0666\dots }=-0,0\left(6\right).$

2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước

Khi làm tròn số đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.

Ví dụ:

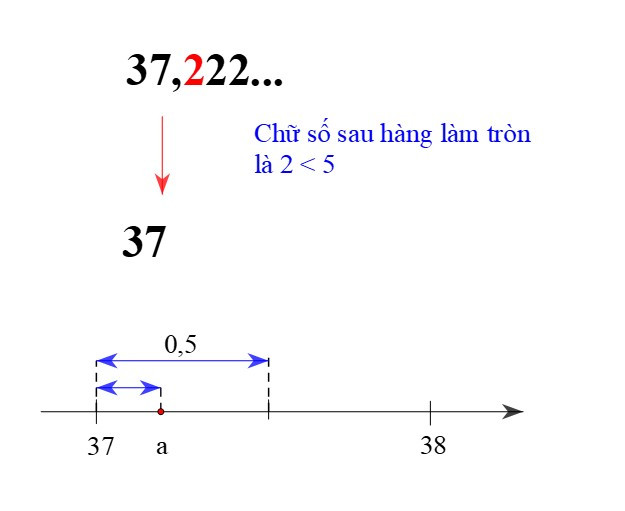
+ Làm tròn a = 37,222… đến hàng đơn vị thì được kết quả là 37. Ta viết 37,222… ≈ 37. Ta cũng nói rằng 37 là kết quả làm tròn của a = 37,222… với độ chính xác là 0,5.

+ Làm tròn số 17,213… đến hàng phần mười ta được kết quả 17,213… ≈ 17,2 với độ chính xác là 0,05.

+ Để làm tròn số 129,18 với độ chính xác là 5, ta làm tròn đến hàng chục. Ta được 129,18 ≈ 130.

Chú ý:

• Muốn làm tròn số thập phân với độ chính xác cho trước, ta có thể xác định hàng làm tròn thích hợp bằng cách sử dụng bảng dưới đây.

Hàng làm tròn	Độ chính xác
Trăm	50
Chục	5
Đơn vị	0,5
Phần mười	0,05
Phần trăm	0,005

Đọc thêm

• Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân hữu hạn. Ví dụ:

$\frac{3}{10}=\frac{3}{2.5}=0,3$

• Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó được viết dưới dạng số thập phân vô hạn tuần hoàn. Ví dụ:

$\frac{1}{14}=\frac{1}{2.7}=0,\mathrm{0714285714285\dots }$

• Mỗi số thập phân vô hạn tuần hoàn biểu diễn một số hữu tỉ. Ví dụ:

$0,\left(1\right)=\frac{1}{9}$; $0,\left(01\right)=\frac{1}{99}$; $0,\left(21\right)=\frac{21}{99}$; $0,\left(9\right)=1$.