50 Bài tập Hàm số liên tục (có đáp án)- Toán 11

Bài tập Toán 11 Chương 4 Bài 3: Hàm số liên tục – Toán 11

A. Bài tập Hàm số liên tục

I. Bài tập trắc nghiệm

Bài 1: Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:

A. Chỉ (I) và (III).

QUẢNG CÁO

B. Chỉ (I) và (II).

C. Chỉ (I).

D. Chỉ (II)

Lời giải:

Chọn đáp án B

Bài 2: Cho hàm số . Tìm k để f(x) gián đoạn tại x= 1.

A. k ≠ ±2.

B. k ≠ 2.

C. k ≠ -2.

QUẢNG CÁO

D. k ≠ ±1.

Lời giải:

Chọn đáp án A

Bài 3: Cho hàm số . Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại x = 1

B. Hàm số liên tục tại mọi điểm

C. Hàm số không liên tục tại x = 1

D. Tất cả đều sai

Lời giải:

Chọn đáp án C

Bài 4: Chọn giá trị f(0) để các hàm số  liên tục tại điểm x= 0.

A. 1

B. 2

C. 3

D. 4

Lời giải:

Chọn đáp án A

Bài 5: Cho hàm số . Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại x₀ = 0

B. Hàm số liên tục tại mọi điểm nhưg gián đoạn tại x₀ = 0

C. Hàm số không liên tục tại x₀ = 0

D. Tất cả đều sai

Lời giải:

Chọn đáp án A

Bài 6: Cho hàm số . Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại x₀ = 2

B. Hàm số liên tục tại mọi điẻm

C. Hàm số không liên tục tại x₀ = 2

D. Tất cả đều sai

Lời giải:

Chọn đáp án C

Bài 7: Cho hàm số . Tìm m để f(x) liên tục trên [0; +∞) là.

A. $\frac{1}{3}$

B. $\frac{1}{2}$

C. $\frac{1}{6}$

D. 1

Lời giải:

Chọn đáp án C

Bài 8: Cho hàm số . Giá trị của a để f(x) liên tục trên R là:

A. 1 và 2.

B. 1 và -1

C. -1 và 2.

D. 1 và -2

Lời giải:

Chọn đáp án D

Bài 9: Cho hàm số  Kết luận nào sau đây là đúng?

A. Hàm số f(x) liên tục tại điểm x = -2

B. Hàm số f(x) liên tục tại điểm x = 0

C. Hàm số f(x) liên tục tại điểm x = 0,5

D. Hàm số f(x) liên tục tại điểm x = 2

Lời giải:

Hàm số đã cho không xác định tại x = 0, x = -2, x = 2 nên không liên tục tại các điểm đó. Hàm số liên tục tại x = 0,5 vì nó thuộc tập xác định của hàm phân thức f(x).

Chọn đáp án C

Bài 10: Cho  với x ≠ 0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu để hàm số f(x) liên tục tại x=0?

Lời giải:

Chọn đáp án C

II. Bài tập tự luận có lời giải

Bài 1: Cho hàm số  với x ≠ 2 . Giá trị của m để f(x) liên tục tại x =2 là:

Lời giải:

Bài 2: Cho hàm số . Tìm b để f(x) liên tục tại x = 3.

Lời giải:

Bài 3: Cho hàm số . Khẳng định nào sau đây đúng nhất.

Lời giải:

Bài 4: Cho phương trình (1) .Chọn khẳng định đúng?

A. Phương trình (1) có đúng một nghiệm trên khoảng (-1; 3).

B. Phương trình (1) có đúng hai nghiệm trên khoảng (-1; 3).

C. Phương trình (1) có đúng ba nghiệm trên khoảng (-1; 3).

D. Phương trình (1) có đúng bốn nghiệm trên khoảng (-1; 3).

Lời giải:

Do đó phương trình có ít nhất 4 ngiệm thuộc khoảng (-1; 3).

Mặt khác phương trình bậc 4 có tối đa bốn nghiệm.

Vậy phương trình có đúng 4 nghiệm thuộc khoảng (-1; 3).

Bài 5: Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:

A. Chỉ (I).

B. Chỉ (III)

C. Chỉ (I) và (III)

D. Chỉ (II) và (III)

Lời giải:

Bài 6: Dùng định nghĩa xét tính liên tục của hàm số f(x) = x³+2x-1 tại x₀=3.

Lời giải:

Bài 7

b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x₀=2.

Lời giải:

Bài 8: 

a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm sso trên tập xác định của nó.

b. Khẳng định nhận xét trên bằng 1 chứng minh.

Lời giải:

a. Đồ thị hàm số (hình bên). Từ đồ thị ta thấy số gián đoạn tại x = -1.

Cho các hàm số  và g(x) = tan(x) + sin(x)

Bài 9 Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.

Lời giải:

Bài 10: Ý kiến sau đúng hay sai?

“Nếu hàm số y = f(x) liên tục tại điểm x₀ và hàm số y = g(x) không liên tục tại x₀, thì y = f(x) + g(x) là một hàm số không liên tục tại x₀“.

Lời giải:

Ý kiến trên đúng, vì y = h(x) = f(x) + g(x) liên tục tại x₀ thì h(x) – f(x) = g(x) liên tục tại x₀ (theo định lý 2 về hàm số liên tục) trái với giả thiết g(x) không liên tục tại x₀.

III. Bài tập vận dụng

Bài 1 Chứng minh rằng phương trình:

a. 2x³ – 6x + 1 = 0 có ít nhất hai nghiệm.

b. cos x = x có nghiệm

Bài 2 Cho hàm số $f(x)=\{\begin{array}{cc}3x+2;& x<-1\\ x^2-1& x\ge -1\end{array}$

a) Vẽ đồ thị của hàm số $y=f(x)$. Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.

b) Khẳng định nhận xét trên bằng một chứng minh.

Bài 3 a. Xét tính liên tục của hàm số $y=g(x)$ tại $x_0=2$, biết 

$g(x)=\{\begin{array}{cc}\frac{x^3-8}{x-2};& x\ne 2\\ 5;& x=2\end{array}$.

b. Trong biểu thức xác định $g(x)$ ở trên, cần thay số $5$ bởi số nào để hàm số liên tục tại $x_0=2$.

Bài 4 Cho hàm số $f(x)=\frac{x+1}{x^2+x-6}$ và $g(x)=tanx+sinx$.

Bài 5 Ý kiến sau đúng hay sai ?

“Nếu hàm số $y=f(x)$ liên tục tại điểm $x_0$ còn hàm số $y=g(x)$ không liên tục tại $x_0$ thì 
$y=f(x)+g(x)$ là một hàm số không liên tục tại $x_0$” 

Bài 6 Chứng minh rằng phương trình:

a) $2x^3-6x+1=0$ có ít nhất hai nghiệm;

b) $cosx=x$ có nghiệm.

Bài 7 Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:

Bài 8 Cho hàm số . Tìm k để f(x) gián đoạn tại x= 1

Bài 9 Cho hàm số . Khẳng định nào sau đây đúng nhất

Bài 10 Chọn giá trị f(0) để các hàm số  liên tục tại điểm x= 0.

B. LÝ THUYẾT HÀM SỐ LIÊN TỤC

I. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM

QUẢNG CÁO

Định nghĩa 1

Cho hàm số y = f(x) xác định trên khoảng K và x₀ ∈ K.

Hàm số y = f(x) được gọi là liên tục tại x₀ nếu $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left({\mathrm{x}}_0\right).$

Ví dụ 1. Xét tính liên tục của hàm số $\mathrm{f}\left(\mathrm{x}\right)=\frac{2\mathrm{x}}{\mathrm{x}-1}$ tại x₀ = 2.

Giải

Hàm số đã cho xác định trên $\mathrm{ℝ}\backslash \left\{1\right\}$.

Do đó hàm số xác định trên khoảng $\left(1;+\infty \right)$ chứa x₀ = 2. Khi đó ta có:

$\underset{\mathrm{x}\to 2}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 2}{\lim }\frac{2\mathrm{x}}{\mathrm{x}-1}=\frac{4}{1}=4=\mathrm{f}\left(2\right)$.

Vậy hàm số y = f(x) liên tục tại x₀ = 2.

II. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG

 

Định nghĩa 2

Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và $\underset{\mathrm{x}\to {\mathrm{a}}^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{a}\right),\underset{\mathrm{x}\to {\mathrm{b}}^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{b}\right).$

Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.

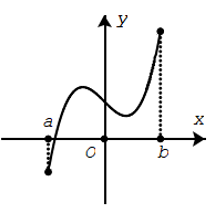
Hàm số liên tục trên khoảng (a;b)

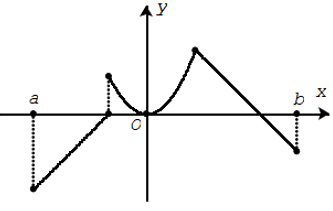
Hàm số không liên tục trên khoảng (a; b).

III. MỘT SỐ ĐỊNH LÍ CƠ BẢN

Định lí 1

 a) Hàm số đa thức liên tục trên toàn bộ tập số thực .

 b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2

Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀;

b) Hàm số $\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}$ liên tục tại x₀ nếu g(x₀) ≠ 0.

Ví dụ 2. Cho hàm số $\mathrm{y}=\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}\frac{{\mathrm{x}}^2-2\mathrm{x}-3}{\mathrm{x}-3}\mathrm{khi}\text{ x}\ne \text{3}\\ \text{4 khi x = 3}\end{array}\right.$ trên tập xác định của nó.

Giải

Tập xác định $\mathrm{D}=\mathrm{ℝ}$

– Nếu x = 3, ta có f(3) = 4, $\underset{\mathrm{x}\to 3}{\lim }\frac{{\mathrm{x}}^2-2\mathrm{x}-3}{\mathrm{x}-3}=\underset{\mathrm{x}\to 3}{\lim }\frac{\left(\mathrm{x}-3\right)\left(\mathrm{x}+1\right)}{\mathrm{x}-3}$$=\underset{\mathrm{x}\to 3}{\lim }\left(\mathrm{x}+1\right)=4=\mathrm{f}\left(3\right)$

Do đó f(x) liên tục tại x = 3.

– Nếu $\mathrm{x}\ne 3$ thì $\mathrm{f}\left(\mathrm{x}\right)=\frac{{\mathrm{x}}^2-2\mathrm{x}-3}{\mathrm{x}-3}$ là hàm phân thức hữu tỉ nên liên tục trên các khoảng $\left(-\infty ;3\right),\left(3;+\infty \right)$.

Vậy hàm số y = f(x) liên tục trên $\mathrm{ℝ}$.

Định lí 3

Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0.

Định lí 3 có thể phát biểu theo một dạng khác như sau:

Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).

Ví dụ 3. Chứng minh rằng phương trình x⁵ – 3x – 7 = 0 luôn có nghiệm.

Giải

Xét hàm f(x) = x⁵ – 3x – 7

Ta có: f(0) = – 7, f(2) = 19. Do đó f(0).f(2) = (-7).19 < 0.

Vì hàm số f(x) là hàm đa thức nên liên tục trên $\mathrm{ℝ}$. Do đó hàm số f(x) liên tục trên [0;2]. Từ đó suy ra phương trình f(x) = 0 có ít nhất một nghiệm $x_0\in \left(0;2\right)$.

Vậy phương trình đã cho luôn có nghiệm.