Cho hình thoi ABCD cạnh 5 và ABC^=60o. Tính: 2AB→+2AD→.

Câu hỏi:

Cho hình thoi ABCD cạnh 5 và $\widehat{ABC}={60}^o$. Tính: $\left|2\overrightarrow{AB}+2\overrightarrow{AD}\right|$.

A. 10;

Đáp án chính xác

B. $\frac{5\sqrt{3}}{2}$;

C. 5;

D. $5\sqrt{3}$.

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: A.

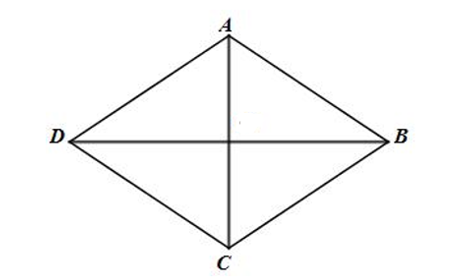
Ta có: $2\overrightarrow{AB}+2\overrightarrow{AD}=2\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=2\overrightarrow{AC}$     (áp dụng quy tắc hình bình hành)
Xét tam giác ABC có:
$\widehat{ABC}={60}^o$
AB = BC (do ABCD là hình thoi)
Do đó, tam giác ABC là tam giác đều
⇒ AC = AB = BC = 5
Vậy $\left|2\overrightarrow{AB}+2\overrightarrow{AD}\right|=\left|2\overrightarrow{AC}\right|=\left|2\right|\left|\overrightarrow{AC}\right|=2.AC=2.5=10$.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tam giác đều ABC cạnh 4. Vectơ −12BC→ có độ dài là.
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC cạnh 4. Vectơ $-\frac{1}{2}\overrightarrow{BC}$ có độ dài là.

   A. 2

   Đáp án chính xác

   B. 4

   C. 3

   D. 6

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: A.
   Do tam giác ABC đều cạnh 4 nên: AB = AC = BC = 4    
   ⇒ $\left|\overrightarrow{BC}\right|=BC$= 4
   Ta có: $\left|-\frac{1}{2}\overrightarrow{BC}\right|=\left|-\frac{1}{2}\right|.\left|\overrightarrow{BC}\right|=\frac{1}{2}.4=2$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình vuông ABCD tâm O cạnh 3. Ta có 12AC→+12DB→ = ?
   
   

   Câu hỏi:
   

   Cho hình vuông ABCD tâm O cạnh 3. Ta có $\left|\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{DB}\right|$ = ?

   A. 2

   B. 4

   C. 3

   Đáp án chính xác

   D. 6

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: C.
   Do O là tâm của hình vuông ABCD nên O là trung điểm của AC và BD nên ta có:
   $\frac{1}{2}\overrightarrow{AC}=\overrightarrow{AO}$; $\frac{1}{2}\overrightarrow{DB}=\overrightarrow{OB}$.
   $\Rightarrow \frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{DB}=\overrightarrow{AO}+\overrightarrow{OB}=\overrightarrow{AB}$
   $\Rightarrow \left|\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{DB}\right|=\left|\overrightarrow{AB}\right|=AB=3$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình thoi ABCD cạnh 5 và ABC^=60o. Tính: 2AB→−2AD→.
   
   

   Câu hỏi:
   

   Cho hình thoi ABCD cạnh 5 và $\widehat{ABC}={60}^o$. Tính: $\left|2\overrightarrow{AB}-2\overrightarrow{AD}\right|$.

   A. 10;

   B. $\frac{5\sqrt{3}}{2}$;

   C. 5;

   D. $10\sqrt{3}$.

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: D.
   
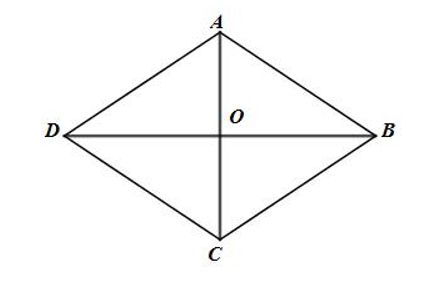
   Ta có: $2\overrightarrow{AB}-2\overrightarrow{AD}=2\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=2\overrightarrow{DB}$ (hiệu hai vectơ).
   Gọi O là giao hai đường chéo của hình thoi, khi đó O là trung điểm của AC và BD. Hơn nữa hai đường chéo này vuông góc với nhau tại O.
   Xét tam giác ABC có:
   $\widehat{ABC}={60}^o$
   AB = BC (do ABCD là hình thoi)
   Do đó, tam giác ABC là tam giác đều
   ⇒ AC = AB = BC = 5
   $\Rightarrow AO=\frac{1}{2}AC=\frac{1}{2}.5=2,5$
   Xét tam giác AOB vuông tại O, theo định lí Pytahgore ta có:
   $A{B}^2=A{O}^2+B{O}^2\Rightarrow B{O}^2=A{B}^2-A{O}^2=5^2-2,5^2=18,75$ 
   $\Rightarrow BO=\frac{5\sqrt{3}}{2}$
   $\Rightarrow BD=2BO=2.\frac{5\sqrt{3}}{2}=5\sqrt{3}$ 
   Vậy $\left|2\overrightarrow{AB}-2\overrightarrow{AD}\right|=\left|2\overrightarrow{DB}\right|=\left|2\right|\left|\overrightarrow{DB}\right|=2DB=2.5\sqrt{3}=10\sqrt{3}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ 12DB→.
   
   

   Câu hỏi:
   

   Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ $\frac{1}{2}\overrightarrow{DB}$.

   A. 5

   B. 2,5

   Đáp án chính xác

   C. 1,5

   D. 2

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: B.
   
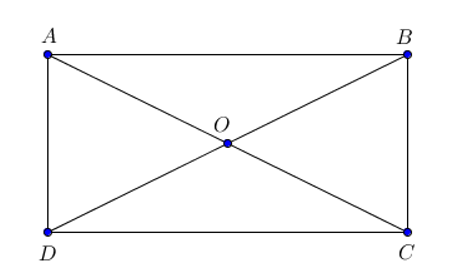
   Xét tam giác ABD vuông tại A (do ABCD là hình chữ nhật)
   Áp dụng định lí Pythagore ta có:
   BD² = AB² + AD² = 4² + 3² = 25 ⇔ BD = 5
   Có: $\left|\frac{1}{2}\overrightarrow{DB}\right|=\left|\frac{1}{2}\right|\left|\overrightarrow{DB}\right|=\frac{1}{2}DB=\frac{1}{2}.5=2,5$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: 12CB→+MA→.
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: $\left|\frac{1}{2}\overrightarrow{CB}+\overrightarrow{MA}\right|$.

   A. a;

   Đáp án chính xác

   B. 3a;

   C. 2a;

   D. 4a.

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: A.
   
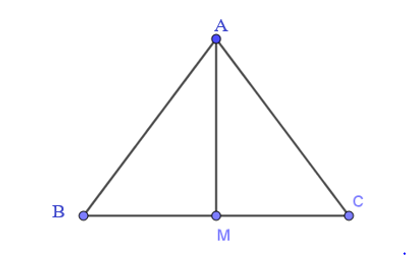
   Do M là trung điểm của BC nên ta có: $\frac{1}{2}\overrightarrow{CB}=\overrightarrow{CM}$ 
   Do đó, ta có: $\frac{1}{2}\overrightarrow{CB}+\overrightarrow{MA}=\overrightarrow{CM}+\overrightarrow{MA}=\overrightarrow{CA}$
   Vậy $\left|\frac{1}{2}\overrightarrow{CB}+\overrightarrow{MA}\right|=\left|\overrightarrow{CA}\right|=CA=a$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====