Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: PB→+PC→+PD→=3AP→.

Câu hỏi:

Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: $\vec{P B} + \vec{P C} + \vec{P D} = 3 \vec{A P}$ .

A. P là trung điểm của AG;

Đáp án chính xác

B. P là trung điểm của AC;

C. P là trung điểm của AD;

D. P là trung điểm của AB.

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: A.
Vì G là trọng tâm của tam giác BCD nên với điểm P thì $\vec{P B} + \vec{P C} + \vec{P D} = 3 \vec{P G}$ .
Ta có:
$\vec{P B} + \vec{P C} + \vec{P D} = 3 \vec{A P}$
$\Leftrightarrow \vec{P B} + \vec{P C} + \vec{P D} - 3 \vec{A P} = \vec{0}$
$\Leftrightarrow 3 \vec{P A} + (\vec{P B} + \vec{P C} + \vec{P D}) = \vec{0}$
$\Leftrightarrow 3 \vec{P A} + 3 \vec{P G} = \vec{0}$
$\Leftrightarrow \vec{P A} + \vec{P G} = \vec{0}$ .
Vậy P là trung điểm của AG.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Điểm I thỏa mãn IA→+2IB→=0→ là:

Câu hỏi:

Điểm I thỏa mãn $\vec{I A} + 2 \vec{I B} = \vec{0}$ là:

A. I nằm trên nửa đường thẳng AB theo hướng từ B về A với $I A = \frac{2}{3} A B$ ;

Đáp án chính xác

B. I nằm trên nửa đường thẳng AB theo hướng từ A về B với $I A = \frac{2}{3} A B$ ;

C. I nằm trên nửa đường thẳng song song với AB theo hướng từ B về A với $I A = \frac{2}{3} A B$ ;

D. I nằm trên nửa đường thẳng AB theo hướng từ B về A với $I A = \frac{1}{3} A B$ .

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: A.
Theo quy tắc ba điểm, ta có: $\vec{I A} + 2 \vec{I B} = \vec{I A} + 2 (\vec{I A} + \vec{A B}) = 3 \vec{I A} + 2 \vec{A B}$ .
Mà $\vec{I A} + 2 \vec{I B} = \vec{0}$
Do đó: $3 \vec{I A} + 2 \vec{A B} = \vec{0}$
$\Leftrightarrow \vec{I A} = - \frac{2}{3} \vec{A B} \Leftrightarrow \vec{I A} = \frac{2}{3} \vec{B A}$
Vậy I nằm trên nửa đường thẳng AB theo hướng từ B về A với $I A = \frac{2}{3} A B$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Điểm K thỏa mãn: KA→+2KB→=CB→ là:

Câu hỏi:

Điểm K thỏa mãn: $\vec{K A} + 2 \vec{K B} = \vec{C B}$ là:

A. K là trung điểm của BC;

B. K là trọng tâm của tam giác ABC;

Đáp án chính xác

C. K là trực tâm của tam giác ABC;

D. K là trung điểm của AB.

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
$\vec{K A} + 2 \vec{K B} = \vec{C B}$
$\Leftrightarrow \vec{K A} + 2 \vec{K B} - \vec{C B} = \vec{0}$
$\Leftrightarrow \vec{K A} + \vec{K B} + (\vec{K B} + \vec{B C}) = \vec{0}$
$\Leftrightarrow \vec{K A} + \vec{K B} + \vec{K C} = \vec{0}$
Vậy K là trọng tâm của tam giác ABC.

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho tam giác ABC. Điểm P thỏa mãn CP→=KA→+2KB→−3KC→ với K tùy ý là điểm thỏa mãn:

Câu hỏi:

Cho tam giác ABC. Điểm P thỏa mãn $\vec{C P} = \vec{K A} + 2 \vec{K B} - 3 \vec{K C}$ với K tùy ý là điểm thỏa mãn:

A. $\vec{C P} = \vec{C A} + 2 \vec{C B}$

Đáp án chính xác

B. $\vec{C P} = \vec{C A} - 2 \vec{C B}$

C. $\vec{C P} = 2 \vec{C A} + 2 \vec{C B}$

D. $\vec{C P} = 2 \vec{C A} - 2 \vec{C B}$

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
$\vec{C P} = \vec{K A} + 2 \vec{K B} - 3 \vec{K C}$
$\Leftrightarrow \vec{C P} = (\vec{K C} + \vec{C A}) + 2 (\vec{K C} + \vec{C B}) - 3 \vec{K C}$ (quy tắc ba điểm)
$\Leftrightarrow \vec{C P} = \vec{C A} + 2 \vec{C B}$
Vậy tập hợp điểm P thỏa mãn $\vec{C P} = \vec{C A} + 2 \vec{C B}$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn OB→+4OC→=2OD→

Câu hỏi:

Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn $\vec{O B} + 4 \vec{O C} = 2 \vec{O D}$

A. O là đỉnh của hình bình hành IBON với $\vec{I N} = \frac{5}{3} \vec{I C}$ ;

B. O là đỉnh của hình bình hành IBON với $\vec{I N} = \frac{4}{3} \vec{I C}$ ;

Đáp án chính xác

C. O là đỉnh của hình bình hành IBON với $\vec{I N} = \vec{I C}$ ;

D. O là đỉnh của hình bình hành IBON với $\vec{I N} = \frac{2}{3} \vec{I C}$ .

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
$\vec{O B} + 4 \vec{O C} = 2 \vec{O D}$
$\Leftrightarrow \vec{O B} + 4 (\vec{O B} + \vec{B C}) = 2 (\vec{O B} + \vec{B D})$ (quy tắc ba điểm)
$\Leftrightarrow 3 \vec{O B} = 2 \vec{B D} - 4 \vec{B C}$
$\Leftrightarrow 3 \vec{O B} = 2 (\vec{B D} - \vec{B C}) - 2 \vec{B C}$ (quy tắc trừ hai vectơ)
$\Leftrightarrow 3 \vec{O B} = 2 \vec{B D} - 4 \vec{B C}$
$\Leftrightarrow 3 \vec{O B} = 2 \vec{B D} + 4 \vec{C B}$
$\Leftrightarrow 3 \vec{O B} = 2 (\vec{C B} + \vec{B D}) + 2 \vec{C B}$
$\Leftrightarrow 3 \vec{O B} = 2 \vec{C D} + 2 \vec{C B}$ (quy tắc ba điểm)
$\Leftrightarrow 3 \vec{O B} = 4 \vec{C I}$ (do I là trung điểm của BD nên $\vec{C D} + \vec{C B} = 2 \vec{C I}$ )
$\Leftrightarrow \vec{O B} = \frac{4}{3} \vec{C I}$

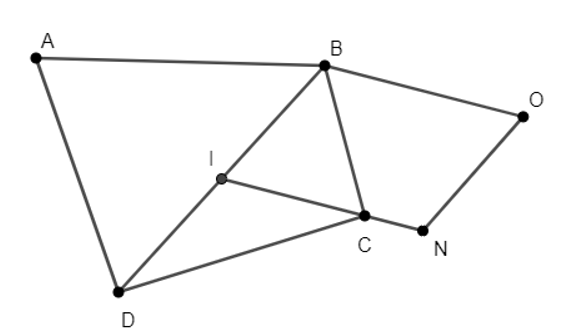
Vậy O là đỉnh của hình bình hành IBON với $\vec{I N} = \frac{4}{3} \vec{I C}$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho tứ giác ABCD và điểm O bất kì sao cho OB→+4OC→−2OD→=0→. Tìm điểm M thỏa mãn hệ thức MB→+4MC→−2MD→=3MA→.

Câu hỏi:

Cho tứ giác ABCD và điểm O bất kì sao cho $\vec{O B} + 4 \vec{O C} - 2 \vec{O D} = \vec{0}$ . Tìm điểm M thỏa mãn hệ thức $|\vec{M B} + 4 \vec{M C} - 2 \vec{M D}| = |3 \vec{M A}|$ .

A. M thuộc đường trung trực của đoạn thẳng OA;

Đáp án chính xác

B. M thuộc đường trung trực của đoạn thẳng DA;

C. M thuộc đường trung trực của đoạn thẳng CA;

D. M thuộc đường trung trực của đoạn thẳng CD.

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
$|\vec{M B} + 4 \vec{M C} - 2 \vec{M D}| = |3 \vec{M A}|$
$\Leftrightarrow |(\vec{M O} + \vec{O B}) + 4 (\vec{M O} + \vec{O C}) - 2 (\vec{M O} + \vec{O D})| = |3 \vec{M A}|$ (quy tắc ba điểm)
$\Leftrightarrow |3 \vec{M O} + (\vec{O B} + 4 \vec{O C} - 2 \vec{O D})| = |3 \vec{M A}|$
$\Leftrightarrow |3 \vec{M O}| = |3 \vec{M A}|$ (do $\vec{O B} + 4 \vec{O C} - 2 \vec{O D} = \vec{0}$ )
$\Leftrightarrow |\vec{M O}| = |\vec{M A}|$
⇔ MO = MA.
Vậy M thuộc đường trung trực của đoạn thẳng OA.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Bài liên quan:

Leave a Comment Hủy