Giải SGK Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh

Giải bài tập Toán lớp 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

A. Câu hỏi trong bài

Giải Toán 7 trang 80 Tập 2

Câu hỏi khởi động trang 80 Toán 7 Tập 2: Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’; BC = B’C’; CA = C’A’.

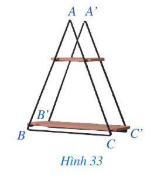
Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Tam giác ABC có bằng tam giác A’B’C’ hay không?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Xét tam giác ABC và tam giác A’B’C’ có:

AB = A’B’; BC = B’C’; CA = C’A’ (giả thiết)

Suy ra ∆ABC = ∆A’B’C’ (c.c.c)

Vậy ∆ABC = ∆A’B’C’.

Hoạt động 1 trang 80 Toán 7 Tập 2: Cho hai tam giác ABC và A’B’C’ (Hình 34) có: AB = A’B’ = 2 cm, AC = A’C’ = 3 cm, BC = B’C’ = 4 cm.

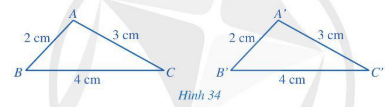
Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Hãy sử dụng thước đo góc để kiểm nghiệm rằng: $\hat{A} = \hat{A^{‘}};$ $\hat{B} = \hat{B^{‘}};$ $\hat{C} = \hat{C^{‘}} .$

Lời giải:

Dùng thước đo góc ta đo được:

+ Trong tam giác ABC: $\hat{A} \approx 104 °,$ $\hat{B} \approx 47 °, \hat{C} \approx 29 °$

+ Trong tam giác A’B’C’: $\hat{A^{‘}} \approx 104 °,$ $\hat{B^{‘}} \approx 47 °, \hat{C^{‘}} \approx 29 °$

Vậy $\hat{A} = \hat{A^{‘}};$ $\hat{B} = \hat{B^{‘}};$ $\hat{C} = \hat{C^{‘}} .$

Giải Toán 7 trang 81 Tập 2

Luyện tập 1 trang 81 Toán 7 Tập 2: Hai tam giác ở Hình 37 có bằng nhau không? Vì sao?

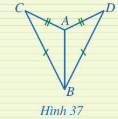
Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Lời giải:

$∆$ ABC, M ∈ BC

∆AMB = ∆AMC.

a) M là trung điểm của BC;

b) Tia AM là tia phân giác của góc BAC và $A M ⊥ B C .$

Chứng minh (Hình 37):

Xét tam giác ABC và tam giác ABD có:

AB là cạnh chung; AC = AD; BC = BD

Suy ra ∆ABC = ∆ABD (c.c.c)

Vậy ∆ABC = ∆ABD.

Giải Toán 7 trang 82 Tập 2

Hoạt động 2 trang 82 Toán 7 Tập 2: Cho hai tam giác vuông ABC và A’B’C’ có: $\hat{A} = \hat{A^{‘}} = 90 °,$ AB = A’B’ = 3 cm, BC = B’C’ = 5 cm (Hình 39). So sánh độ dài các cạnh AC và A’C’.

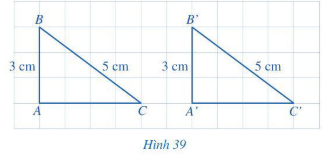
Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Lời giải:

Giả sử cạnh hình vuông nhỏ trong hình vẽ có độ dài bằng a (cm).

Quan sát hình vẽ ta thấy: Cạnh AB và cạnh A’B’ có độ dài bằng 3 lần độ dài của cạnh hình vuông.

Mà AB = A’B’ = 3 cm nên 3a = 3 suy ra a = 1 (cm)

Lại có AC = 4a = 4.1 = 4 (cm) và A’C’ = 4a = 4.1 = 4 (cm)

Do đó AC = A’C’ (= 4cm)

Vậy AC = A’C’.

B. Bài tập

Giải Toán 7 trang 83 Tập 2

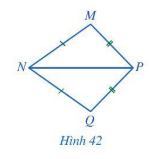
Bài 1 trang 83 Toán 7 Tập 2: Cho Hình 42 có MN = QN, MP = QP. Chứng minh rằng $\hat{M N P} = \hat{Q N P}$

Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Lời giải:

$∆$ MNP, ∆QNP

MN = QN, MP = QP

$\hat{M N P} = \hat{Q N P} .$

Chứng minh (Hình 42):

Xét tam giác MNP và tam giác QNP có:

MN = QN (giả thiết); MP = QP (giả thiết); NP là cạnh chung.

Suy ra $∆$ MNP = $∆$ QNP (c.c.c)

Do đó $\hat{M N P} = \hat{Q N P}$ (hai góc tương ứng)

Vậy $\hat{M N P} = \hat{Q N P}$

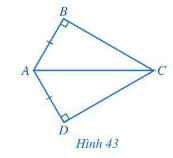
Bài 2 trang 83 Toán 7 Tập 2: Cho Hình 43 có AB = AD, $\hat{A B C} = \hat{A D C} = 90 ° .$ Chứng minh $\hat{A C B} = \hat{A C D} .$

Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Lời giải:

$∆$ ABC, ∆ADC

AB = AD

$\hat{A B C} = \hat{A D C} = 90 ° .$

$\hat{A C B} = \hat{A C D} .$

Chứng minh (Hình 43):

Vì $∆$ ABC có $\hat{A B C} = 90 °$ (giả thiết) nên $∆$ ABC vuông tại B.

Vì ∆ADC có $\hat{A D C} = 90 °$ (giả thiết) nên ∆ADC vuông tại D.

Xét hai tam giác ABC (vuông tại B) và tam giác ADC (vuông tại D) có:

AC là cạnh chung

AB = AD (giả thiết)

Suy ra $∆$ ABC = ∆ADC (cạnh huyền – cạnh góc vuông)

Do đó $\hat{A C B} = \hat{A C D}$ (hai góc tương ứng)

Vậy $\hat{A C B} = \hat{A C D}$

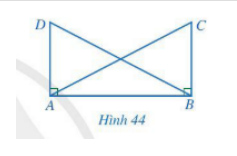
Bài 3 trang 83 Toán 7 Tập 2: Cho Hình 44 có AC = BD, $\hat{A B C} = \hat{B A D} = 90 ° .$ Chứng minh AD = BC.

Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Lời giải:

$∆$ ABC, ∆ABD

AC = BD, $\hat{A B C} = \hat{B A D} = 90 ° .$

AD = BC

Chứng minh (Hình 44):

Vì $\hat{A B C} = \hat{B A D} = 90 °$ nên $∆$ ABC vuông tại B và $∆$ ABD vuông tại A.

Xét tam giác ABC (vuông tại B) và tam giác BAD (vuông tại A) có:

AB là cạnh chung

AC = BD (giả thiết)

Suy ra $∆$ ABC = $∆$ BAD (cạnh huyền – cạnh góc vuông)

Do đó BC = AD (hai cạnh tương ứng)

Vậy BC = AD.

Bài 4 trang 83 Toán 7 Tập 2: Cho hai tam giác ABC và MNP thoả mãn: AB = MN, BC = NP, AC = MP, $\hat{A} = 65 °, \hat{N} = 71 ° .$ Tính số đo các góc còn lại của hai tam giác.

Lời giải:

$∆$ ABC, ∆MNP

AB = MN, BC = NP, AC = MP; $\hat{A} = 65 °, \hat{N} = 71 ° .$

Tính số đo của $\hat{B}, \hat{C}, \hat{M}, \hat{P} .$

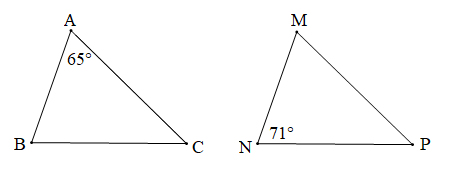
Giải Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (ảnh 1)

Xét tam giác ABC và tam giác MNP có:

AB = MN (giả thiết)

BC = NP (giả thiết)

AC = MP (giả thiết)

Suy ra ∆ABC = ∆MNP (c.c.c)

Nên $\hat{A} = \hat{M}, \hat{B} = \hat{N}, \hat{C} = \hat{P}$ (các cặp góc tương ứng)

Mà $\hat{A} = 65 °, \hat{N} = 71 °$ (giả thiết)

Do đó $\hat{M} = 65 °, \hat{B} = 71 °$

Xét tam giác ABC với $\hat{A} = 65 °,$ $\hat{B} = 71 °$ ta có:

$\hat{A} + \hat{B} + \hat{C} = 180 °$ (tổng ba góc trong một tam giác)

Suy ra $\hat{C} = 180 ° - \hat{A} - \hat{B}$

Hay $\hat{C} = 180 ° - 65 ° - 71 ° = 44 °$

Suy ra $\hat{P} = 44 °$

Vậy $\hat{M} = 65 °, \hat{B} = 71 °, \hat{C} = 44 °$ và $\hat{P} = 44 ° .$

====== ****&**** =====

Bài liên quan:

Leave a Comment Hủy