Câu hỏi:
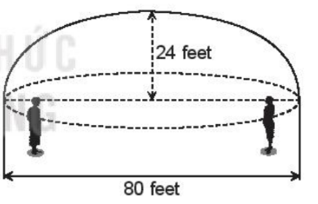
Hình vẽ bên minh hoạ một phòng thì thầm (whispering gallery) với mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet. Một âm thanh được phát ra từ một tiêu điểm của phòng thì thầm có thể được nghe thấy tại tiêu điểm còn lại. Hỏi hai người nói thầm qua lại với nhau thì sẽ cách trung tâm của phòng bao nhiêu mét ? Theo đơn vị đo lường quốc tế, 1 feet = 0,3048 m.
Trả lời:
Hướng dẫn giải
Theo đề bài, mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet nên mặt cắt của phòng thì thầm là một nửa elip có a = 40 feet, b = 24 feet nên\(c = \sqrt {{a^2} – {b^2}} = \sqrt {{{40}^2} – {{24}^2}} = 32\) feet
Vậy nếu hai người nói chuyện với nhau trong phòng thì sẽ cách trung tâm phòng một nửa tiêu cự là c = 32 feet = 32 . 0,3048 m = 9,7536 m.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hypebol?
A. 16×2 – 5y2 = –80;
B. x2 = 4y;
C. \(\frac{{{x^2}}}{4} – \frac{{{y^2}}}{1} = 1\);
D. \(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1\).
Câu hỏi:
Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hypebol?
A. 16x2 – 5y2 = –80;
B. x2 = 4y;
C. \(\frac{{{x^2}}}{4} – \frac{{{y^2}}}{1} = 1\);
D. \(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{1} = 1\).Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Phương trình chính tắc của đường hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\). (trong đó a, b > 0)
Do đó, \(\frac{{{x^2}}}{4} – \frac{{{y^2}}}{1} = 1\) là một phương trình chính tắc của đường hypebol.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai điểm A(–1; 0) và B(–2; 3). Phương trình đường thẳng đi qua B và vuông góc với AB là
A. x – 3y + 11 = 0;
B. x – 3y + 1 = 0;
C. –x – 3y + 7 = 0;
D. 3x + y + 3 = 0.
Câu hỏi:
Cho hai điểm A(–1; 0) và B(–2; 3). Phương trình đường thẳng đi qua B và vuông góc với AB là
A. x – 3y + 11 = 0;
B. x – 3y + 1 = 0;
C. –x – 3y + 7 = 0;
D. 3x + y + 3 = 0.Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Đường thẳng đi qua B và vuông góc với AB nhận vectơ \(\overrightarrow {AB} = ( – 1;3)\) là vectơ pháp tuyến.
Phương trình đường thẳng đi qua B và vuông góc với AB là:
–1(x + 2) + 3(y – 3) = 0
⇔ –x + 3y – 2 – 9 = 0
⇔ x – 3y + 11 = 0.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho điểm A(2; 3) và đường thẳng d: x + y + 3 = 0. Khoảng cách từ điểm A đến đường thẳng d là
A.\(\frac{6}{{\sqrt {13} }}\);
B. \(4\sqrt 2 \);
C. 8;
D. \(2\sqrt 2 \).
Câu hỏi:
Cho điểm A(2; 3) và đường thẳng d: x + y + 3 = 0. Khoảng cách từ điểm A đến đường thẳng d là
A.\(\frac{6}{{\sqrt {13} }}\);
B. \(4\sqrt 2 \);
C. 8;
D. \(2\sqrt 2 \).Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Khoảng cách từ điểm A đến đường thẳng d là:
d(A, d) = \(\frac{{\left| {2 + 3 + 3} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{8}{{\sqrt 2 }} = 4\sqrt 2 \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai đường thẳng d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0. Góc giữa hai đường thẳng d và k là
A. 30°;
B. 135°;
C. 45°;
D. 60°.
Câu hỏi:
Cho hai đường thẳng d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0. Góc giữa hai đường thẳng d và k là
A. 30°;
B. 135°;
C. 45°;
D. 60°.Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Xét d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0 có các vectơ pháp tuyến lần lượt là:
\(\overrightarrow {{n_d}} = (1; – 2)\)
\(\overrightarrow {{n_k}} = (1;3)\)
Gọi φ là góc giữa hai đường thẳng d và k.
Ta có: \(\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_d}} ;\overrightarrow {{n_k}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_d}} .\overrightarrow {{n_k}} } \right|}}{{\left| {\overrightarrow {{n_d}} } \right|\left| {\overrightarrow {{n_k}} } \right|}}\)\( = \frac{{\left| {1.1 + ( – 2).3} \right|}}{{\sqrt {{1^2} + {{( – 2)}^2}} .\sqrt {{1^2} + {3^2}} }} = \frac{5}{{5\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\)
\( \Rightarrow \varphi = 45^\circ \)
Vậy góc giữa hai đường thẳng là φ = 45°.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường tròn (C) có phương trình (x – 2)2 + (y + 3)2 = 9. Tâm I và bán kính R của đường tròn (C) là
A. I(2; –3), R = 9;
B. I(–2; 3), R = 3;
C. I(–2; 3), R = 9;
D. I(2; –3), R = 3.
Câu hỏi:
Cho đường tròn (C) có phương trình (x – 2)2 + (y + 3)2 = 9. Tâm I và bán kính R của đường tròn (C) là
A. I(2; –3), R = 9;
B. I(–2; 3), R = 3;
C. I(–2; 3), R = 9;
D. I(2; –3), R = 3.Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Xét phương trình đường tròn: (x – 2)2 + (y + 3)2 = 9 ta có:
Tâm I(2; –3)
Bán kính: R = \(\sqrt 9 \) = 3.====== **** mời các bạn xem câu tiếp bên dưới **** =====