Câu hỏi:
Tính tầm xa của quả bóng chày, tức là khoảng cách từ mặt đất ở chỗ đánh bóng và nơi quả bóng chạm đất (kết quả làm tròn đến hàng đơn vị).
Trả lời:
Hướng dẫn giải
Bóng chạm đất khi y = 0.
Xét y = 0 ⇔ \(\frac{{ – 1}}{{125}}{x^2}\) + x + 1 = 0 ⇔ x ≈ 126 hoặc x ≈ – 1 (loại).
Vậy tầm xa của quả bóng chày là khoảng 126 m.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho các mệnh đề:
P: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”.
Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, . Xét tính đúng sai của các mệnh đề này.
Câu hỏi:
Cho các mệnh đề:
P: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”.
Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, . Xét tính đúng sai của các mệnh đề này.Trả lời:
Hướng dẫn giải
+ Mệnh đề P ⇒ Q: “Nếu phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt thì phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”. Đây là mệnh đề đúng.
+ Mệnh đề Q ⇒ P: “ Nếu phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0 thì phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”. Đây là mệnh đề đúng.
+ Mệnh đề P ⇔ Q: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt khi và chỉ khi phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”. Do P ⇒ Q, Q ⇒ P đều là các mệnh đề đúng nên mệnh đề P ⇔ Q là mệnh đề đúng.
+ Mệnh đề
Mệnh đề là mệnh đề phủ định của mệnh đề P và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt”.
Mệnh đề là mệnh đề phủ định của mệnh đề Q và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”.
Khi đó, ta phát biểu mệnh đề : “Nếu phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt thì phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”. Mệnh đề này là mệnh đề đúng.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.
Câu hỏi:
Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.
Trả lời:
Hướng dẫn giải
+ Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt là điều kiện đủ để phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0.
+ Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0 là điều kiện cần để phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Gọi X là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.
Câu hỏi:
Gọi X là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.
Trả lời:
Hướng dẫn giải
Ta có các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu thì luôn có hai nghiệm trái dấu, hiển nhiên đây là hai nghiệm phân biệt. Nhưng các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt thì hai nghiệm này chưa chắc đã trái dấu.
Do đó mọi phần tử của tập hợp Y thì đều là phần tử của tập hợp X.
Vậy Y là tập con của tập hợp X và ta viết Y ⊂ X.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x – 2y \ge – 6}\\{2x + y \le 10}\end{array}} \right.\).
Câu hỏi:
Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x – 2y \ge – 6}\\{2x + y \le 10}\end{array}} \right.\).Trả lời:
Hướng dẫn giải
Ta xác định miền nghiệm của từng bất phương trình trong hệ đã cho như sau:
Bước 1: Trục Oy có phương trình x = 0 và điểm (1; 0) thỏa mãn 1 > 0. Do đó miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (miền không bị gạch).
Bước 2: Trục Ox có phương trình y = 0 và điểm (0; 1) thỏa mãn 1 > 0. Do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (miền không bị gạch).
Bước 3: Vẽ đường thẳng d1: 3x – 2y = – 6. Lấy điểm O(0; 0) không thuộc d1 và thay x = 0, y = 0 vào biểu thức 3x – 2y ta được: 3 . 0 – 2 . 0 = 0 > – 6. Do đó, miền nghiệm của bất phương trình 3x – 2y ≥ – 6 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0) (miền không bị gạch).
Bước 4: Vẽ đường thẳng d2: 2x + y = 10. Lấy điểm O(0; 0) không thuộc d2 và thay x = 0, y = 0 vào biểu thức 2x + y ta được: 2 . 0 + 0 = 0 < 10. Do đó, miền nghiệm của bất phương trình 2x + y ≤ 10 là nửa mặt phẳng bờ d2 chứa điểm O(0; 0) (miền không bị gạch).
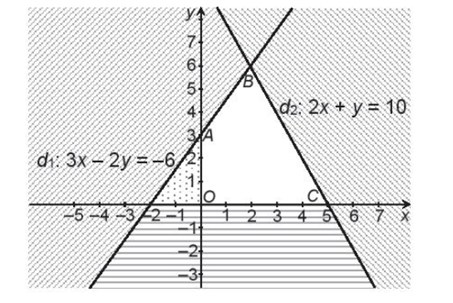
Vậy miền nghiệm D của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch), trong đó A(0; 3), B(2; 6), C(5; 0), như hình vẽ sau:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.
Câu hỏi:
Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.
Trả lời:
Hướng dẫn giải
Vì giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D, do đó ta tính giá trị của F tại (x; y) là tọa độ các đỉnh O, A, B, C.
Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0;
F(0; 3) = 2 . 0 + 3 . 3 = 9;
F(2; 6) = 2 . 2 + 3 . 6 = 22;
F(5; 0) = 2 . 5 + 3 . 0 = 10.
Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D lần lượt là 22 và 0.====== **** mời các bạn xem câu tiếp bên dưới **** =====