Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Đường cao AH của tam giác cắt đường tròn ở D. Vẽ đường kính AE.a) Chứng minh rằng BECD là hình thang cân.b) Gọi M là điểm chính giữa của cung DE, OM cắt BC tại I. Chứng minh rằng I là trung điểm của BC.c) Tính bán kính của đường tròn biết BC = 24cm, IM = 8cm.

Câu hỏi:

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Đường cao AH của tam giác cắt đường tròn ở D. Vẽ đường kính AE.a) Chứng minh rằng BECD là hình thang cân.b) Gọi M là điểm chính giữa của cung DE, OM cắt BC tại I. Chứng minh rằng I là trung điểm của BC.c) Tính bán kính của đường tròn biết BC = 24cm, IM = 8cm.

Trả lời:

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho ∆ABC vuông cân tại A và nội tiếp trong đường tròn (O). Chứng minh rằnga) AB⏜=BC⏜b) AB⏜<BC⏜
   
   

   Câu hỏi:
   

   Cho $∆$ABC vuông cân tại A và nội tiếp trong đường tròn (O). Chứng minh rằnga) $\stackrel{⏜}{\mathrm{AB}}=\stackrel{⏜}{\mathrm{BC}}$b) $\stackrel{⏜}{\mathrm{AB}}<\stackrel{⏜}{\mathrm{BC}}$

   Trả lời:

   Trong đường tròn (O):Xét $∆$ABC vuông cân tại A, ta có ngay:- AB = AC (hai cạnh bên của tam giác cân) => $\stackrel{⏜}{\mathrm{AB}}=\stackrel{⏜}{\mathrm{BC}}$– AB < BC (cạnh góc vuông nhỏ hơn cạnh huyền) => $\stackrel{⏜}{\mathrm{AB}}<\stackrel{⏜}{\mathrm{BC}}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. a) Vẽ đường tròn tâm (O), bán kính R = 2 cm. Nêu cách vẽ cung AB⏜ có số đo bằng 600. Hỏi dây AB dài bao nhiêu xen – ti – mét?b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như hình dưới
   
   

   Câu hỏi:
   

   a) Vẽ đường tròn tâm (O), bán kính R = 2 cm. Nêu cách vẽ cung $\stackrel{⏜}{\mathrm{AB}}$ có số đo bằng ${60}^0$. Hỏi dây AB dài bao nhiêu xen – ti – mét?b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như hình dưới

   Trả lời:

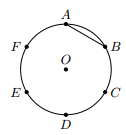
   b)Vậy các điểm A, B, C, D, E, F chia đường tròn thành 6 cung bằng nhau.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho đường tròn (O), dây AB. Gọi M là điểm chính giữa của cung AB. Vẽ dây MC cắt dây AB tại D. Vẽ đường vuông góc với AB tại D, cắt OC ở K. Chứng minh rằng  là tam giác cân.
   
   

   Câu hỏi:
   

   Cho đường tròn (O), dây AB. Gọi M là điểm chính giữa của cung AB. Vẽ dây MC cắt dây AB tại D. Vẽ đường vuông góc với AB tại D, cắt OC ở K. Chứng minh rằng  là tam giác cân.

   Trả lời:

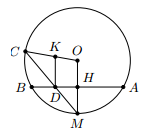   Vì M là điểm chính giữa của cung AB nênSuy ra <=> $∆\mathrm{KCD}$ là tam giác cân

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Chứng minh rằng hai cung chắn giữa hai dây song song thì bằng nhau.
   
   

   Câu hỏi:
   

   Chứng minh rằng hai cung chắn giữa hai dây song song thì bằng nhau.

   Trả lời:

   Xét hai dây song song AB và CD, kẻ bán kính $\mathrm{ON}\perp \mathrm{AB}$, khi đó vì:

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại hai điểm A và B. Kẻ các đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’). Gọi E là giao điểm thứ hai của AC với đường tròn (O’)a) So sánh các cung nhỏ BC⏜, BD⏜.b) Chứng minh rằng B là điểm chính giữa của cung EBD⏜ (tức là điểm B chia cung EBD⏜ thành hai cung bằng nhau BE⏜= BD⏜)
   
   

   Câu hỏi:
   

   Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại hai điểm A và B. Kẻ các đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’). Gọi E là giao điểm thứ hai của AC với đường tròn (O’)a) So sánh các cung nhỏ $\stackrel{⏜}{\mathrm{BC}}, \stackrel{⏜}{\mathrm{BD}}$.b) Chứng minh rằng B là điểm chính giữa của cung $\stackrel{⏜}{\mathrm{EBD}}$ (tức là điểm B chia cung $\stackrel{⏜}{\mathrm{EBD}}$ thành hai cung bằng nhau $\stackrel{⏜}{\mathrm{BE}}= \stackrel{⏜}{\mathrm{BD}}$)

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====