Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM với AB, và K là giao điểm của EM với AC. Chứng minh:a) Ba điểm D, A, E thẳng hàng.b) Tứ giác IAKM là hình chữ nhật.c) Tam giác DME là tam giác vuông cân.

Câu hỏi:

Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM với AB, và K là giao điểm của EM với AC. Chứng minh:a) Ba điểm D, A, E thẳng hàng.b) Tứ giác IAKM là hình chữ nhật.c) Tam giác DME là tam giác vuông cân.

Trả lời:

a) Chứng minh $\widehat{DEA}={180}^0$b) Chứng minh$\widehat{AIM}=\widehat{AKM}=\widehat{IAK}={90}^0$c) Chứng minh DDME có $\widehat{EDM}=\widehat{DEM}={45}^0$Þ DDME vuông cân ở M.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điẻm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?
   
   

   Câu hỏi:
   

   Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điẻm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?

   Trả lời:

   Sử dụng tính chất đường trung bình của tam giácChứng minh: HEFG là hình bình hành và EF ^ HEÞ HEFG là hình chữ nhật.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M Î AB). Chứng minh tứ giác PCQM là hình chữ nhật.
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M Î AB). Chứng minh tứ giác PCQM là hình chữ nhật.

   Trả lời:

   Chứng minh: PM = CQ Mà PM//CQÞ PCQM là hình bình hànhLại có: $\widehat{C}={90}^0$ Þ PCQM là hình chữ nhật

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
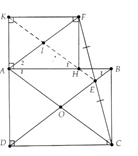
3. Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:a) Tứ giác AHFK là hình chữ nhật;b) AF song song với BD;c) Ba điểm E, H, K thẳng hàng
   
   

   Câu hỏi:
   

   Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:a) Tứ giác AHFK là hình chữ nhật;b) AF song song với BD;c) Ba điểm E, H, K thẳng hàng

   Trả lời:

   a) $\widehat{FHA}=\widehat{HAK}=\widehat{AKF}={90}^0$Þ AHFK là hình chữ nhật.b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACFÞ AF//OEÞ AF/BDc) Gọi I là giao điểm của AF và HK.Chứng minh$\widehat{H_1}={\widehat{A}}_1(\widehat{H_1}=\widehat{A_2}=\widehat{B_1}=\widehat{A_1})\Rightarrow KH//AC$ mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.Mà E là trung điểm của FC Þ K, H, E thẳng hàng

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
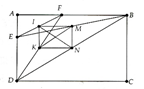
4. Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM
   
   

   Câu hỏi:
   

   Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM

   Trả lời:

   HS chứng minh IMNK là hình chữ nhật Þ IN = KM

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
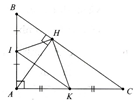
5. Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:a) IHK^=900. b) Chu vi DIHK bằng nửa chu vi DABC.
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:a) $\widehat{IHK}={90}^0.$ b) Chu vi DIHK bằng nửa chu vi DABC.

   Trả lời:

   a) Chứng minh:  $\widehat{IAH}=\widehat{IHA},\widehat{HAK}=\widehat{AHK}\Rightarrow \widehat{IHA}+\widehat{AHK}={90}^0\Rightarrow \widehat{IHK}={90}^0$b) Chú ý: Sử dụng tính chất đường trung bình của tam giác và sử dụng. c) HS tự chứng minh

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====