Cho tam giác ABC và một điểm M nằm trên cạnh BC. Khi điểm M di chuyển trên cạnh BC thì trung điểm I của đoạn thẳng AM di chuyển trên đường nào?

Câu hỏi:

Cho tam giác ABC và một điểm M nằm trên cạnh BC. Khi điểm M di chuyển trên cạnh BC thì trung điểm I của đoạn thẳng AM di chuyển trên đường nào?

Trả lời:

Khi M º B thì I là trung điểm của AC. Vậy khi I di chuyển trên đoạn AB thì M di chuyển trên đoạn thẳng I”I’ là đường trung bình của DABC (với I’ và I” lần lượt là trung điểm của AC và AB)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Lý thuyết Đường thẳng song song với một đường thẳng cho trước (mới 2023 + bài tập) – Toán 8
   Lý thuyết Đường thẳng song song với một đường thẳng cho trước

   A. Lý thuyết

   1. Khoảng cách giữa hai đường thẳng song song

   Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia. h là khoảng cách giữa hai đường thẳng song song a và b.

   

   2. Tính chất của các điểm cách đều một đoạn thẳng cho trước

   Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.

   Nhận xét: Từ định nghĩa về khoảng cách hai đường thẳng song song và tính chất trên ta có: Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.

   3. Đường thẳng song song cách đều

   Định lí:

   + Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.

   + Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

   B. Bài tập tự luyện

   Bài 1: Cho Δ ABC có D là trung điểm của AB, kẻ DE//BC ( E \in AC ). Chứng minh rằng AE = EC.

   Hướng dẫn:

   

   Do DE//BC theo giả thiết nên vẽ thêm Ax//DE thì

   Ax//DE//BC       ( 1 )

   Vì D là trung điểm của AB nên AD = BD       ( 2 )

   Từ ( 1 ), ( 2 ) suy ra ba đường Ax, DE, BC là ba đường song song cách đều nên nó chắn trên đường thẳng AC hai đoạn thẳng liên tiếp bằng nhau là AE = EC.

   Bài 2: Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K lần lượt là các chân đường cao kẻ từ kẻ từ B và C đến đường thẳng DE. Chứng minh rằng HE = DK.

   Hướng dẫn:

   

   Vì BD, CE là đường cao của tam giác ABC nên

   do đó Δ BDC vuông tại D, Δ CEB vuông tại E.

   Gọi M là trung điểm của BC

   ⇒ DM, EM là đường trung tuyến ứng với cạnh huyền của Δ BDC và Δ CEB.

   Áp dụng tính chất của đường trung tuyến ứng với cạnh huyền của hai tam giác trên ta được:

   

   Từ giả thiết ta có tứ giác BHKC là hình thang vuông nên vẽ MI ⊥ DE thì BH//MI//CK ( 1 ) (vì cùng vuông góc với đường thẳng DE)

   Mà ta có BM = MC ( 2 ) (do ta vẽ hình trên)

   Từ ( 1 ),( 2 ) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK ( 3 ).

   Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được:

   EI = ID ( 4 )

   Trừ theo vế đẳng thức ( 3 ) cho ( 4 ), ta được: HE = DK.
2. Giáo án Luyện tập Đường thẳng song song với một đường thẳng cho trước (2023) – Toán 8
   Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

   Giáo án Luyện tập Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước

   A. Mục tiêu

   1. Kiến thức:

   – Nắm được khái niệm khoảng cách giữa 2 đường thẳng song song, tính chất của các điểm cách 1 đường thẳng cho trước.

   2. Kỹ năng:

   – Biết cách vận dụng định lý về đường thẳng song song cách đều để chứng minh các đường thẳng bằng nhau. Biết cách chứng tỏ 1 điểm nằm trên 1 đường thẳng song song với 1 đường thẳng cho trước.

   – Vận dụng các kiến thức đã học vào giải toán ứng dụng trong thực tế.

   3. Thái độ:

   – Tích cực, tự giác, hợp tác.

   4. Phát triển năng lực:

   – Biết vận dụng kiến thức để vẽ hình và tính khoảng cách giữa 2 đường thẳng, giải được 1 số bài toán thực tế/

   B. Chuẩn bị

   1. Giáo viên:

   – Phấn màu, thước thẳng, compa.

   2. Học sinh:

   – Thước thẳng, ôn tập lại kiến thức về khoảng cách từ 1 điểm tới 1 đường thẳng.

   C. Phương pháp

   – Vấn đáp, nêu và giải quyết vấn đề, thuyết trình, …

   D. Tiến trình dạy học

   1. Tổ chức lớp: Kiểm diện.

   2. Kiểm tra bài cũ: kết hợp trong tiết luyện tập.

   3. Bài mới

   Hoạt động của giáo viên

   Hoạt động của học sinh

   Ghi bảng

   Hoạt động 1: Khởi động (8’)
   – Treo bảng phụ ghi đề kiểm tra – Gọi một HS lên bảng – Cả lớp cùng làm bài – Kiểm tra bài tập về nhà của HS – Cho HS nhận xét – GV hoàn chỉnh và cho điểm Chốt lại các nội dung chính của bài…	– HS đọc yêu cầu đề kiểm tra – Một HS lên bảng trả lời làm – HS khác nhận xét – Tự sửa sai (nếu có)	1. Phát biểu định nghĩa về khoảng cách giữa hai đường thẳng song song. 2. Phát biểu về tính chất của các điểm cách đều một đường thẳng cho trước. 3. Cho CC’//DD’//EB và AC = CD = DE. Chứng minh AC’ = C’D’ = D’B
   Hoạt động 2: Luyện tập (35’)
   Bài 71 trang 103 SGK – Cho HS đọc đề bài, vẽ hình và tóm tắt GT-KL a) Muốn A, O, M thẳng hàng ta cần chứng minh điều gì ? – Để O là trung điểm của AM ta cần làm gì ? – Cho HS hợp tác nhóm để làm câu a. Thời gian làm bài là 5’ – Gọi một HS giải ở bảng – Theo dõi HS làm bài – Cho cả lớp nhận xét ở bảng – GV hoàn chỉnh bài giải của HS hoặc ghi lời giải tóm tắt … b) Hướng dẫn: – Gọi P là trung điểm AB ⇒ ? – Gọi Q là trung điểm AC ⇒ ? ⇒ điều gì ? – Khi M di chuyển thì di chuyển trên đường nào ? c) Đường vuông góc và đường xiên đường nào ngắn hơn ? – AH là đường gì ? – AM là đường gì ? – Nên ta có điều gì ? – Vậy AM nhỏ nhất khi nào ? – Lúc đó M ở vị trí nào ? – Gọi HS lên bảng trình bày – Cho HS tham gia nhận xét – GV sửa sai cho các em hoặc trình bày nhanh lời giải mẫu các câu a, b, c ghi sẳn trên bảng phụ	– HS đọc đề bài, vẽ hình, ghi GT-KL – O là trung điểm của AM – Ta cần chứng minh ADME là hình chữ nhật – HS suy nghĩ cá nhân sau đó chia nhóm hoạt động a) Ta có  (gt) Tứ giác ADME là hình chữ nhật (có 3 góc vuông). Mà O là trung điểm của đường chéo DE Nên O cũng là trung điểm của đường chéo AM. Do đó A, O, M thẳng hàng. – HS tham gia nhận xét – HS sửa bài vào vở b) – OP // BM (OP là đường trung bình ) – OQ// MC (OQ là đường trung bình) – O thuộc đường trung bình PQ – Khi M di chuyển thì O di chuyển trên đường trung bình PQ c) Đường vuông góc ngắn hơn đường xiên – AH là đường vuông góc kẻ từ A đến BC – AM là đường xiên kẻ từ A đến BC – AM ≥ AH – AM = AH – M trùng với H – HS lên bảng trình bày – HS khác nhận xét – HS sửa bài vào vở	Bài 71 trang 103 SGK Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE Bài tập tương tự Cho tam giác ABC. Kẻ đường cao BD và CE. H là trực tâm của tam giác. Gọi M, N, P theo theo thứ tự là trung điểm của các đoạn thẳng BC,DE, AH. Chứng minh M,N,P thẳng hàng
   Hoạt động 3: Vận dụng-mở rộng (2’)
   GV yêu cầu HS nahwcs lại tập hợp    + Đường thẳng song song với 1 đường thẳng cho trước.    + Đường trung trực của 1 đoạn thẳng.

   4.  Hướng dẫn học sinh tự học (3p)

   – Ôn tập lại các đ/n, t/c, dấu hiệu nhận biết của HBH, tính chất của tam giác cân.

   – Học và làm bài tập 72 SGK.

   – Chuẩn bị bài: Hình thoi.
3. Giải SGK Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước
   Giải bài tập Toán lớp 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước

   Trả lời câu hỏi giữa bài

   Câu hỏi 1 trang 100 Toán lớp 8 Tập 1: Cho hai đường thẳng song song a và b (h.93).

   Gọi A và B là hai điểm bất kì thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b. Gọi độ dài AH là h. Tính độ dài BK theo h.

   

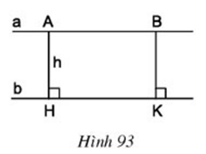
   Lời giải

   Ta có: $\left.\begin{array}{l}AH\perp b\\ BK\perp b\end{array}\right\}\Rightarrow AH//BK$

   Vì a // b nên AB // HK

   ⇒ tứ giác ABKH là hình bình hành

   ⇒ AH = BK = h.

   Vậy BK = h.

   Câu hỏi 2 trang 101 Toán lớp 8 Tập 1: Cho đường thẳng b. Gọi a và a’ là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h (h.94), (I) và (II) là các nửa mặt phẳng bờ b. Gọi M, M’ là các điểm cách đường thẳng b một khoảng bằng h, trong đó M thuộc nửa mặt phẳng (I), M’ thuộc nửa mặt phẳng (II). Chứng minh rằng $M\in a,M‘\in a‘.$

   

   Lời giải

   Xét tứ giác AMKH, có:

   $\left.\begin{array}{l}AH\perp b\\ MK\perp b\end{array}\right\}\Rightarrow AH//MK$

   AH = MK = h

   Suy tứ giác AMKH là hình bình hành

   $\Rightarrow$AM // HK hay AM // b

   Mà đường thẳng a qua A cũng song song với b nên theo tiên đề Ơ – clit suy ra AM trùng đường thẳng a hay M thuộc a.

   Xét tứ giác A’M’K’H’, có:

   $\left.\begin{array}{l}A‘H‘\perp b\\ M‘K‘\perp b\end{array}\right\}\Rightarrow A‘H‘//M‘K‘$

   A’H’ = M’K’ = h

   Suy tứ giác A’M’K’H’ là hình bình hành

   $\Rightarrow$A’M’ // H’K’ hay A’M’ // b

   Mà đường thẳng a’ qua A’ cũng song song với b nên theo tiên đề Ơ – clit suy ra A’M’ trùng đường thẳng a’ hay M’ thuộc a’.

   Câu hỏi 3 trang 101 Toán lớp 8 Tập 1: Xét các tam giác ABC có BC cố định, đường cao ứng với cạnh BC luôn bằng 2 cm (h.95). Đỉnh A của các tam giác đó nằm trên đường nào?

   

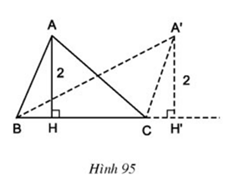
   Lời giải

   Tam giác ABC có AH là đường cao và AH  = 2 cm nghĩa là điểm A cách đường thẳng BC một khoảng bằng 2.

   Tập hợp các điểm A cách đường thẳng BC một khoảng bằng 2 là đường thẳng song song với BC và cách BC một khoảng bằng 2cm.

   Câu hỏi 4 trang 102 Toán lớp 8 Tập 1: Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau.

   Chứng minh rằng:

   a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.

   b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.

   

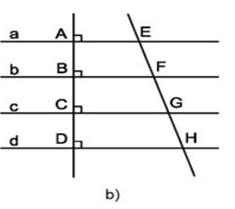
   Lời giải

   a) Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD

   ⇒ B là trung điểm của AC; C là trung điểm của BD

   Xét hình thang AEGC (AE // GC) có:

   B là trung điểm của AC  

   BF // AE // GC

   ⇒ F là trung điểm EG (định lí đường trung bình của hình thang)

   ⇒ EF = FG (1)

   Xét hình thang BFHD (BF // HD) có:

   C là trung điểm của BD 

   BF // GC // DH

   ⇒ G là trung điểm FH (định lí đường trung bình của hình thang)

   ⇒ GH = FG (2)

   Từ (1) và (2) suy ra EF = FG = GH.

   b) Ta có: EF = FG = GH

   ⇒ F là trung điểm của EG; G là trung điểm của FH

   Xét hình thang AEGC (AE // GC) có:

   F là trung điểm của EG

   BF // AE // GC

   ⇒ B là trung điểm AC (định lí đường trung bình của hình thang)

   ⇒ AB = BC (3)

   Xét hình thang BFHD (BF // HD) có:

   G là trung điểm của FH

   BF // GC // DH

   ⇒ C là trung điểm BD (định lí đường trung bình của hình thang)

   ⇒ BC = CD (4)

   Từ (3) và (4) suy ra AB = BC = CD.

   Vậy các đường thẳng a, b, c, d song song và cách đều nhau.

   Bài tập (trang 102, 103)

   Bài 67 trang 102 Toán 8 Tập 1: Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.

   

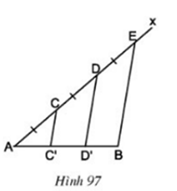
   Lời giải:

   

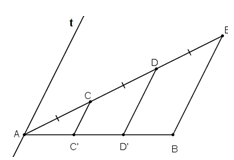
   Kẻ đường thẳng At // CC’ // DD’ // BE như hình vẽ.

   Ta có: AC = CD = DE

   ⇒ At, CC’, DD‘, BE là các đường thẳng song song cách đều

   ⇒ AC’ = C’D’ = D’B

   hay đoạn thẳng AB bị chia ra làm 3 phần bằng nhau.

   Bài 68 trang 102 Toán 8 Tập 1: Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?

   Lời giải

   

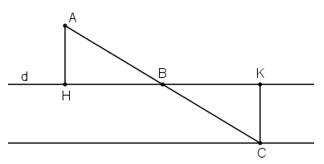
   Gọi H, K là hình chiếu của A và C trên đường thẳng d.

   ⇒ Khoảng cách từ A đến d bằng AH

   ⇒ AH = 2cm.

   Xét ΔAHB vuông tại H và ΔCKB vuông tại K có:

   $\widehat{AHB}=\widehat{CKB}=90°$

   AB = BC (C đối xứng với A qua B)

   $\widehat{ABH}=\widehat{CBK}$ (2 góc đối đỉnh)

   ⇒ ΔAHB = ΔCKB (cạnh huyền – góc nhọn)

   ⇒ CK = AH = 2cm (2 cạnh tương ứng).

   Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm.

   Bài 69 trang 103 Toán 8 Tập 1: Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng:

   (1) Tập hợp các điểm cách A cố định một khoảng 3cm. (2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm.

   (5) Là đường trung trực của đoạn thẳng AB. (6) là hai đường thẳng song song với a và cách a một khoảng 3cm. (7) là đường tròn tâm A bán kính 3cm. (8) là tia phân giác của góc xOy

   Lời giải

   Ghép các ý:

   (1) với (7)

   (2) với (5)

   (3) với (8)

   (4) với (6)

   Bài 70 trang 103 Toán 8 Tập 1: Cho góc vuông xOy, điểm A thuộc tia Oy sao cho OA = 2cm. Lấy B là một điểm bất kì thuộc tia Ox. Gọi C là trung điểm của AB. Khi điểm B di chuyển trên tia Ox thì điểm C di chuyển trên đường nào?

   Lời giải

   

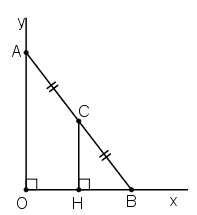
   – Cách 1:

   Kẻ $CH \perp Ox$

   Mà $OA\perp \text{Ox}$

   ⇒ CH // OA

   Xét tam giác AOB, ta có:

   CB = CA (gt) nên C là trung điểm AB

   CH // AO (cùng vuông góc Ox)

   ⇒ H là trung điểm của OB

   ⇒ HO = HB

   ⇒ CH là đường trung bình của tam giác AOB

   ⇒$CH=\frac{AO}{2}=\frac{2}{2}=1cm.$

   Điểm C cách tia Ox cố định một khoảng không đổi 1cm nên C di chuyển trên tia song song với Ox, cách Ox một khoảng bằng 1cm và nằm trong góc xOy.

   – Cách 2:

   Vì C là trung điểm của AB nên OC là trung tuyến ứng với cạnh huyền AB do đó OC = CA.

   Điểm C di chuyển trên đường trung trực của OA.

   Bài 71 trang 103 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.

   a) Chứng minh rằng ba điểm A, O, M thẳng hàng.

   b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?

   c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất?

   Lời giải:

   

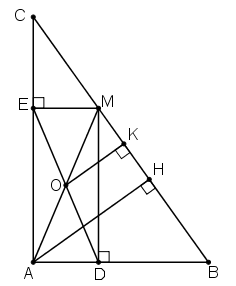
   a) Tứ giác ADME có: $\widehat{EAD}=\widehat{AEM}=\widehat{ADM}=90°$

   ⇒ ADME là hình chữ nhật

   O là trung điểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.

   Vậy A, O, M thẳng hàng.

   b) Kẻ AH ⊥ BC; OK ⊥ BC.

   Ta có OA = OM, OK // AH (cùng vuông góc BC)

   ⇒ MK = KH

   ⇒ OK là đường trung bình của ΔMAH

   $\Rightarrow OK=\frac{AH}{2}$

   ⇒ điểm O cách BC một khoảng cố định bằng $\frac{AH}{2}.$

   ⇒ O nằm trên đường thẳng song song với BC các BC một khoảng bằng $\frac{AH}{2}.$

   Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.

   Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.

   c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).

   Vậy AM nhỏ nhất khi M trùng H.

   Bài 72 trang 103 Toán 8 Tập 1: Đố. Để vạch một đường thẳng song song với mép gỗ AB và cách mép gỗ 10cm, bác thợ mộc đặt đoạn bút chì CD dài 10cm vuông góc với ngón tay trỏ lấy làm cữ (h.98), rồi đưa ngón trỏ chạy dọc theo mép gỗ AB. Căn cứ vào kiến thức nào mà ta kết luận rằng đầu chì C vạch nên đường thẳng song song với AB và cách AB là 10cm?

   

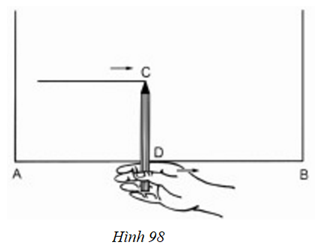
   Lời giải

   – Căn cứ vào tính chất đường thẳng song song với một đường thẳng cho trước.

   – Vì điểm C cách mép gỗ AB một khoảng không đổi bằng 10cm nên khi tay di chuyển thì đầu bút chì C vạch nên một đường thẳng song song với AB và cách AB một khoảng 10cm.
4. Điền vào chỗ trống:          a) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng bằng 2 cm là …          b) Tập hợp đỉnh A các tam giác vuông ABC có cạnh huyền BC cố định và BC = 4cm là …          c) Tập hợp giao điểm O của hai đường chéo của hình chữ nhật ABCD có cạnh BC cố định là …
   
   

   Câu hỏi:
   

   Điền vào chỗ trống:          a) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng bằng 2 cm là …          b) Tập hợp đỉnh A các tam giác vuông ABC có cạnh huyền BC cố định và BC = 4cm là …          c) Tập hợp giao điểm O của hai đường chéo của hình chữ nhật ABCD có cạnh BC cố định là …

   Trả lời:

   a) Hai đường thẳng song song với đường thẳng a và cách đường thẳng a một khoảng là 2cm.b) Đường tròn $\left(O\frac{BC}{2}\right)$ với O là trung điểm của BCc) Đường thẳng trung trực của đoạn BC trừ trung điểm BC.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Điền vào chỗ trống:a) Tập hợp các điểm cách điểm A cố định một khoảng bằng 1 cm là…b) Tập hợp các điểm cách đều hai đầu đoạn thẳng AB cố định là …c) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc là…
   
   

   Câu hỏi:
   

   Điền vào chỗ trống:a) Tập hợp các điểm cách điểm A cố định một khoảng bằng 1 cm là…b) Tập hợp các điểm cách đều hai đầu đoạn thẳng AB cố định là …c) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc là…

   Trả lời:

   a) Đường tròn (A; 1cm)b) Đường trung trực của đoạn thẳng ABc) Tia phân giác trong của $\widehat{xOy}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====