Câu hỏi:
Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM
Trả lời:
HS chứng minh IMNK là hình chữ nhật Þ IN = KM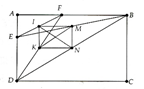
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điẻm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?
Câu hỏi:
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điẻm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?
Trả lời:
Sử dụng tính chất đường trung bình của tam giácChứng minh: HEFG là hình bình hành và EF ^ HEÞ HEFG là hình chữ nhật.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M Î AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Câu hỏi:
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M Î AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Trả lời:
Chứng minh: PM = CQ Mà PM//CQÞ PCQM là hình bình hànhLại có: Þ PCQM là hình chữ nhật
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:a) Tứ giác AHFK là hình chữ nhật;b) AF song song với BD;c) Ba điểm E, H, K thẳng hàng
Câu hỏi:
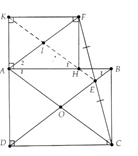
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:a) Tứ giác AHFK là hình chữ nhật;b) AF song song với BD;c) Ba điểm E, H, K thẳng hàng
Trả lời:
a) Þ AHFK là hình chữ nhật.b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACFÞ AF//OEÞ AF/BDc) Gọi I là giao điểm của AF và HK.Chứng minh mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.Mà E là trung điểm của FC Þ K, H, E thẳng hàng
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:a) IHK^=900. b) Chu vi DIHK bằng nửa chu vi DABC.
Câu hỏi:
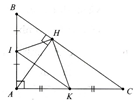
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:a) b) Chu vi DIHK bằng nửa chu vi DABC.
Trả lời:
a) Chứng minh: b) Chú ý: Sử dụng tính chất đường trung bình của tam giác và sử dụng. c) HS tự chứng minh
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.a) Tứ giác AMBQ là hình gì ?b) Chứng minh rằng CH ^ AB.c) Chứng minh tam giác PIQ cân.
Câu hỏi:
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.a) Tứ giác AMBQ là hình gì ?b) Chứng minh rằng CH ^ AB.c) Chứng minh tam giác PIQ cân.
Trả lời:
) HS tự chứng minh AMBQ là hình chữ nhật (ahi đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)b) Sử dụng tính chất trực tâm tam giác.c) Sử dụng tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh
====== **** mời các bạn xem câu tiếp bên dưới **** =====