Câu hỏi:
Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?

Trả lời:
Hướng dẫn giải
+ Tam giác ABC có AB = AC (kí hiệu bằng nhau trên hình)
Do đó, tam giác ABC cân tại đỉnh A.
+ Áp dụng định lí tổng 3 góc trong tam giác DEF, ta có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \)
Suy ra \(\widehat F = 180^\circ – \left( {\widehat D + \widehat E} \right) = 180^\circ – \left( {70^\circ + 50^\circ } \right) = 60^\circ \).
Do đó ta có, \(\widehat D \ne \widehat E \ne \widehat F\). Vậy tam giác DEF không phải tam giác cân.
+ Tam giác MNP có \(\widehat N = \widehat P\,\,\,\left( { = 50^\circ } \right)\).
Do đó, tam giác MNP cân tại đỉnh M.
+ Áp dụng định lí tổng 3 góc trong tam giác KGH, ta có:
\(\widehat K + \widehat G + \widehat H = 180^\circ \)
Suy ra \(\widehat H = 180^\circ – \left( {\widehat K + \widehat G} \right) = 180^\circ – \left( {40^\circ + 70^\circ } \right) = 70^\circ \).
Do đó tam giác KGH có \(\widehat G = \widehat H\, = 70^\circ \).
Vậy tam giác KGH cân tại đỉnh K.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).
Câu hỏi:
Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).

Trả lời:
Hướng dẫn giải
+ Tam giác ABC có AB = AC nên tam giác ABC cân tại đỉnh A.
Suy ra \(\widehat C = \widehat B = 65^\circ \).
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \)
Suy ra \(\widehat A = 180^\circ – \left( {\widehat B + \widehat C} \right) = 180^\circ – \left( {65^\circ + 65^\circ } \right) = 50^\circ \).
+ Tam giác MNP có MN = MP nên tam giác MNP cân tại đỉnh M.
Suy ra \(\widehat M = \widehat N\).
Áp dụng định lí tổng ba góc trong tam giác MNP, ta có:
\(\widehat M + \widehat N + \widehat P = 180^\circ \)
\( \Rightarrow \widehat M + \widehat M = 180^\circ – \widehat P\)\( \Rightarrow 2\widehat M = 180^\circ – \widehat P\)
\( \Rightarrow \widehat M = \frac{{180^\circ – \widehat P}}{2} = \frac{{180^\circ – 75^\circ }}{2} = 52,5^\circ \).
Vậy \(\widehat M = \widehat N = 52,5^\circ \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
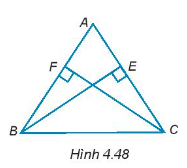
- Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC cân tại đỉnh A.
Câu hỏi:
Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC cân tại đỉnh A.
Trả lời:
Hướng dẫn giải
Tam giác ABE vuông tại E, do đó: \(\widehat A + \widehat {ABE} = 90^\circ \Rightarrow \widehat {ABE} = 90^\circ – \widehat A\).
Tam giác ACF vuông tại F, do đó: \(\widehat A + \widehat {ACF} = 90^\circ \Rightarrow \widehat {ACF} = 90^\circ – \widehat A\).
Từ đó, suy ra \(\widehat {ABE} = \widehat {ACF}\).
Xét tam giác vuông AEB và tam giác vuông AFC có:
BE = CF (theo giả thiết)
\(\widehat {ABE} = \widehat {ACF}\) (cmt)
Do đó, ∆AEB = ∆AFC (cạnh góc vuông và góc nhọn kề nó).
Suy ra AB = AC (hai cạnh tương ứng).
Vậy tam giác ABC cân tại đỉnh A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
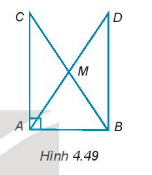
- Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD vuông tại B.
Câu hỏi:
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD vuông tại B.

Trả lời:
Hướng dẫn giải
Xét tam giác AMC và tam giác DMB có:
MA = MD (gt)
MB = MC (M là trung điểm của BC)
\(\widehat {AMC} = \widehat {DMB}\) (hai góc đối đỉnh)
Do đó, ∆AMC = ∆DMB (c – g – c).
Suy ra \(\widehat {DBM} = \widehat {ACM}\) (hai góc tương ứng).
Do tam giác ABC vuông tại A nên \(\widehat {ABC} + \widehat {ACM} = \widehat {ABC} + \widehat {ACB} = 90^\circ \).
Khi đó, ta có: \(\widehat {ABD} = \widehat {ABC} + \widehat {CBD}\)\( = \widehat {ABC} + \widehat {DBM}\)= \(\widehat {ABC} + \widehat {ACM} = 90^\circ \).
Suy ra \(\widehat {ABD} = 90^\circ \).
Vậy tam giác ABD vuông tại B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD = ∆BAC.
Câu hỏi:
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
∆ABD = ∆BAC.
Trả lời:
Hướng dẫn giải:
Xét tam giác vuông ABD và tam giác vuông BAC có:
BD = AC (do ∆AMC = ∆DMB)
AB: cạnh chung
Do đó, ∆ABD = ∆BAC (hai cạnh góc vuông).====== **** mời các bạn xem câu tiếp bên dưới **** =====
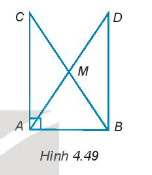
- Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.
Câu hỏi:
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.
Trả lời:
Hướng dẫn giải:
Do tam giác ABC vuông tại A nên AC ⊥ AB tại A.
Tam giác ABD vuông tại B nên DB ⊥ AB tại B.
Suy ra AC // DB (do cùng vuông góc với AB).
\( \Rightarrow \widehat {BDA} = \widehat {CAD}\) (hai góc so le trong).
Lại có: \(\widehat {ACB} = \widehat {BDA}\) (do ∆ABD = ∆BAC).
Do đó, \(\widehat {CAD} = \widehat {ACB}\), hay \(\widehat {CAM} = \widehat {ACM}\).
Suy ra tam giác AMC cân tại đỉnh M.
Khi đó MA = MC.
Mà MB = MC (do M là trung điểm của BC).
Nên MA = MB = MC.
Do đó, tam giác AMB cân tại đỉnh M.====== **** mời các bạn xem câu tiếp bên dưới **** =====