Câu hỏi:
Cho tam giác ABC nhọn có ba đường cao AM, BN, CP. Biết AM = BN = CP. Khi đó tam giác ABC là:
A. Tam giác vuông;
B. Tam giác vuông cân;
C. Tam giác đều;
Đáp án chính xác
D. Tam giác cân.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
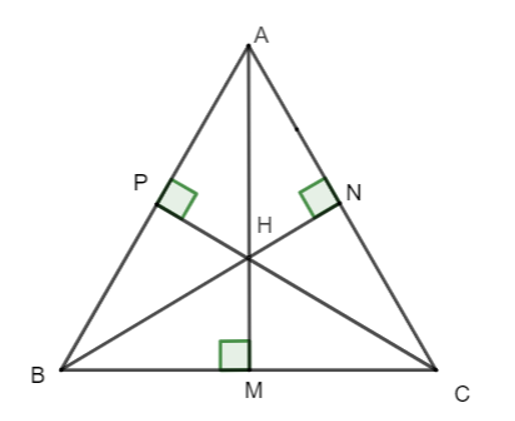
Gọi H là giao điểm của ba đường cao.
Ta có: + = 90°;
+ = 90°;
= (hai góc đối đỉnh).
Do đó = .
Xét ∆ABM vuông tại M và ∆CBP vuông tại P ta có:
= (cmt).
AM = CP (gt).
Do đó ∆ABM = ∆CBP (cạnh góc vuông – góc nhọn).
Suy ra AB = BC (hai cạnh tương ứng) (1)
Chứng minh tương tự ta được ∆BNC = ∆AMC (cạnh góc vuông – góc nhọn)
Suy ra BC = AC (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AB = BC = AC.
Vậy ∆ABC là tam giác đều.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điền vào chỗ trống sau: “Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là … của tam giác đó”.
Câu hỏi:
Điền vào chỗ trống sau: “Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là … của tam giác đó”.
A. Đường trung trực;
B. Đường cao;
Đáp án chính xác
C. Đường trung tuyến;
D. Đường phân giác.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điền vào chỗ trống sau: “Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này được gọi là … của tam giác”.
Câu hỏi:
Điền vào chỗ trống sau: “Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này được gọi là … của tam giác”.
A. Trọng tâm;
B. Trực tâm;
Đáp án chính xác
C. Trung điểm;
D. Trung trực.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
Ba đường cao của một tam giác cùng đi qua một điểm. Điểm này được gọi là trực tâm của tam giác.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em chọn phát biểu đúng.
Câu hỏi:
Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em chọn phát biểu đúng.
A. H là trực tâm của ∆ABC;
B. CH là đường cao của ∆ABC;
C. H là trọng tâm của ∆ABC;
D. Phát biểu A, B đều đúng.
Đáp án chính xác
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
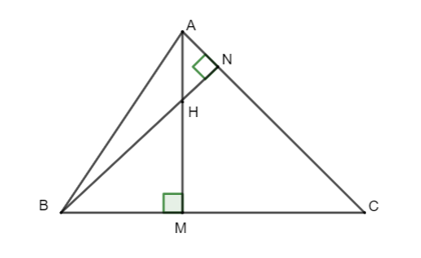
Vì hai đường cao AM và BN cắt nhau tại H nên H là trực tâm của ΔABC và CH là đường cao của ΔABC.
Do đó hai câu A và B đều đúng.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ΔABC có đường cao AM và BN cắt nhau tại H. Chọn câu đúng.
Câu hỏi:
Cho ΔABC có đường cao AM và BN cắt nhau tại H. Chọn câu đúng.
A. CH // AB;
B. CH HB;
C. CH AB;
Đáp án chính xác
D.Tất cả đáp án trên đều sai.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C

Xét ΔABC có:
AM là đường cao (gt);
BN là đường cao (gt);
AM và BN cắt nhau tại H.
Do đó H là trực tâm của ΔABC.
Suy ra CH là đường cao của ΔABC.
Vậy CH AB.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC vuông tại A. Lấy điểm O thuộc AB. Vẽ OM vuông góc với BC tại M. Tia MO cắt AC tại N. Chọn câu đúng.
Câu hỏi:
Cho tam giác ABC vuông tại A. Lấy điểm O thuộc AB. Vẽ OM vuông góc với BC tại M. Tia MO cắt AC tại N. Chọn câu đúng.
A. O là trực tâm của ΔABC;
B. O là trực tâm của ΔMBC;
C. CO vuông góc với NB;
D. Hai đáp án B và C đều đúng.
Đáp án chính xác
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D

Xét ∆NBC có:
NM là đường cao (OMBC, N Î OM);
BA là đường cao (BA NC);
NM cắt BA tại O.
Do đó O là trực tâm của ∆ABC.
Suy ra CO là đường cao của ∆ABC.
Do vậy CO vuông góc với NB.
Vậy đáp án B và C đều đúng.====== **** mời các bạn xem câu tiếp bên dưới **** =====